Gelöste Aufgaben/Kw96: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 58: | Zeile 58: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Ein Stab ''ABC'' ist durch eine lineare veränderliche Streckenlast ''q'' mit den Eckwerten ''q<sub>A</sub>'' in ''A'' und ''q<sub>B</sub>'' in ''B'' sowie dem Moment ''M<sub>B</sub>'' in ''B'' belastet. Der Stab (E-Modul: ''E'') besteht aus zwei Sektionen mit den Längen ''l<sub>1</sub>'' bzw. ''l<sub>2</sub>'' sowie den Flächenmomenten ''I<sub>1</sub>'' bzw. ''I<sub>2</sub>''. Der Stab ist in ''A'' durch ein gelenkiges Festlager, in ''C'' durch eine Schiebehülse gelagert, in ''B'' sind die beiden Sektionen fest miteinander verbunden. Die Feder in ''A'' ist eine Drehfester mit Steifigkeit ''K<sub>A</sub>'', die Federn in ''B'' und ''C'' sind Translationsfedern mit den Steifigkeiten ''k<sub>B</sub>, k<sub>C</sub>''. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kw98-01.png|alternativtext=|links|mini|250x250px|Lageplan]] | ||
Gesucht ist | Gesucht ist die FEM Lösung für den Euler-Bernoulli-Balken unter Verwendung von zwei Finiten Elementen. | ||
</onlyinclude> | </onlyinclude> | ||
[[Datei:Kw98-02.png|mini|Systemparameter]] | |||
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für die angegebenen Parameter: | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
| Zeile 69: | Zeile 72: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir arbeiten mit den Standard-System-Matrizen nach Abschnitt "[[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]]".<!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 80: | Zeile 84: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | System-Parameter sind: | ||
<math>\begin{array}{l} \displaystyle {{q}_{A}}=3000 \frac{N}{m},\\ \displaystyle {\ell_{1}}=\frac{7\cdot m}{10},\\ \displaystyle {{\mathit{EI}}_{1}}=33600 N {{m}^{2}},\\ \displaystyle {\ell_{2}}=\frac{21}{40} m,\\ \displaystyle {{\mathit{EI}}_{2}}=16800 N {{m}^{2}},\\ \displaystyle {{K}_{A}}=96000 N m,\\ \displaystyle {{k}_{C}}=\frac{256}{229}\cdot {{k}_{B}},\\ \displaystyle {{k}_{B}}=\frac{256}{229} N m,\\ \displaystyle {{q}_{B}}=12000\frac{N}{m},\\ \displaystyle {{M}_{B}}=1470 N m \end{array}</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 91: | Zeile 98: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Ansatzfunktion für die Trial-Functions ist ein Polynom 3. Grades: | ||
<math>\mathrm{w}\left( \xi\right) :={{c}_{3}}\cdot {{\xi}^{3}}+{{c}_{2}}\cdot {{\xi}^{2}}+{{c}_{1}}\cdot \xi+{{c}_{0}}</math> | |||
An den Rändern müssen die Auslenkung und Kippung mit den Knoten-Variablen übereinstimmen: | |||
<math>\begin{array}{l} \displaystyle {{c}_{0}}={{W}_{i-1}},\\ \displaystyle \frac{{{c}_{1}}}{{{l}_{i}}}={{\Phi}_{i-1}},\\ \displaystyle {{c}_{3}}+{{c}_{2}}+{{c}_{1}}+{{c}_{0}}={{W}_{i}},\\ \displaystyle \frac{{{c}_{1}}+2\cdot {{c}_{2}}+3\cdot {{c}_{3}}}{{{l}_{i}}}={{\Phi}_{i}} \end{array}</math>[[Datei:Kw96-11.png|alternativtext=Trial-Functions|mini|Trial-Functions]]Damit ist die Ansatzfunktion des Finiten Elements mit den vier Knotenvariablen | |||
<math>w(\xi)\;=\; \ell_i \cdot \Phi_i \cdot \left( \xi-1 \right) \cdot \xi^2+W_{i-1} \cdot \left( \xi-1\right) ^2 \cdot \left( 1+2 \cdot \xi\right)-W_i \cdot \xi^2 \cdot \left( 2\cdot \xi-3\right) +\Phi_{i-1} \cdot \ell_i \cdot \left( \xi-1\right) ^2 \cdot \xi</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text=Text | |text=Text | ||
| Zeile 102: | Zeile 119: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | So sind die Element-Steifigkeitsmatrix | ||
<math>\displaystyle \underline{\underline{K}}_i=\,\frac{EI_i}{\ell_i^3}\begin{pmatrix}12 & 6\cdot {{\ell}_{i}} & -12 & 6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}}\\ -12 & -6\cdot {{\ell}_{i}} & 12 & -6\cdot {{\ell}_{i}}\\ 6\cdot {{\ell}_{i}} & 2\cdot {{\ell}_{i}^{2}} & -6\cdot {{\ell}_{i}} & 4\cdot {{\ell}_{i}^{2}}\end{pmatrix}</math> | |||
die Koordinaten des FE-Modells - hier für das Element "1": | |||
<math>\underline{Q}\,=\,\begin{pmatrix}{{\Phi}_{0}}\\ {{W}_{1}}\\ {{\Phi}_{1}}\\ {{W}_{2}}\end{pmatrix}</math>. | |||
Wir komponieren daraus die System-Steifigkeitsmatrix - durch Aufaddieren der Beiträge der beiden Elemente und Einarbeiten der Randbedingugnen - zu | |||
<math>\underline{\underline{K}}_0 =\begin{pmatrix} {K_A}+\frac{4 {{\mathit{EI}}_1}}{{\ell_1}} & -\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & \frac{2 {{\mathit{EI}}_1}}{{\ell_1}} & 0\\ -\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & {k_B}+\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}+\frac{12 {{\mathit{EI}}_1}}{{{\ell}_{1}^{3}}} & \frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}-\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & -\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}\\ \frac{2 {{\mathit{EI}}_1}}{{\ell_1}} & \frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}-\frac{6 {{\mathit{EI}}_1}}{{{\ell}_{1}^{2}}} & \frac{4 {{\mathit{EI}}_2}}{{\ell_2}}+\frac{4 {{\mathit{EI}}_1}}{{\ell_1}} & -\frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}}\\ 0 & -\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}} & -\frac{6 {{\mathit{EI}}_2}}{{{\ell}_{2}^{2}}} & {k_C}+\frac{12 {{\mathit{EI}}_2}}{{{\ell}_{2}^{3}}}\end{pmatrix}</math> | |||
Wie das geht, steht in Abschnitt [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]].<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text=Text | |text=Text | ||
| Zeile 113: | Zeile 144: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Knotenvariablen sind damit | ||
<math>\begin{array}{ll}W_0 = 0& \\\Phi_0 = 0.00624& \\W_1 = 0.00657 m& \\\Phi_1 = 0.0123& \\W_2 = 0.00846 m& \\\Phi_2 = 0& \end{array}</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 124: | Zeile 159: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Biegelinie des Balkens sieht damit so aus:<!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
| Zeile 141: | Zeile 177: | ||
Version vom 31. März 2021, 10:01 Uhr
Aufgabenstellung
Ein Stab ABC ist durch eine lineare veränderliche Streckenlast q mit den Eckwerten qA in A und qB in B sowie dem Moment MB in B belastet. Der Stab (E-Modul: E) besteht aus zwei Sektionen mit den Längen l1 bzw. l2 sowie den Flächenmomenten I1 bzw. I2. Der Stab ist in A durch ein gelenkiges Festlager, in C durch eine Schiebehülse gelagert, in B sind die beiden Sektionen fest miteinander verbunden. Die Feder in A ist eine Drehfester mit Steifigkeit KA, die Federn in B und C sind Translationsfedern mit den Steifigkeiten kB, kC.
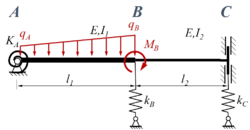
Gesucht ist die FEM Lösung für den Euler-Bernoulli-Balken unter Verwendung von zwei Finiten Elementen.
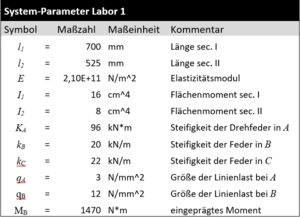
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für die angegebenen Parameter:
Lösung mit Maxima
tmp
Wir arbeiten mit den Standard-System-Matrizen nach Abschnitt "FEM-Formulierung für den Euler-Bernoulli-Balken".
Header
Text
1+1
tmp
System-Parameter sind:
Declarations
Text
1+1
tmp
Die Ansatzfunktion für die Trial-Functions ist ein Polynom 3. Grades:
An den Rändern müssen die Auslenkung und Kippung mit den Knoten-Variablen übereinstimmen:
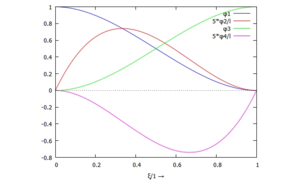
Damit ist die Ansatzfunktion des Finiten Elements mit den vier Knotenvariablen
Formfunctions
Text
1+1
tmp
So sind die Element-Steifigkeitsmatrix
die Koordinaten des FE-Modells - hier für das Element "1":
.
Wir komponieren daraus die System-Steifigkeitsmatrix - durch Aufaddieren der Beiträge der beiden Elemente und Einarbeiten der Randbedingugnen - zu
Wie das geht, steht in Abschnitt Finite Elemente Methode.
Equilibrium Conditions
Text
1+1
tmp
Die Knotenvariablen sind damit
Solving
Text
1+1
tmp
Die Biegelinie des Balkens sieht damit so aus:
Post-Processing
Text
1+1
Links
- ...
Literature
- ...
- Gelöste Aufgaben
- Dimensionslose Schreibweise
- A*x=b
- Lineare Algebra
- Achsensymmetrie
- Rotationssymmetrie
- Analytische Lösung
- Numerische Lösung
- Anfangswertproblem
- Randwertproblem
- Ansys
- Shell-Element
- Arbeitsfunktion
- Potential
- Prinzip der virtuellen Arbeit
- Prinzip der virtuellen Verrückungen
- Prinzip vom Minimum der Potentiellen Energie
- Formänderungsenergie
- Axiom
- Biege-Belastung
- Membranspannung
- Computer
- Stab
- Dehnstab
- Euler-Bernoulli-Balken
- Timoshenko-Balken
- Feder-Masse-System
- Draft
- Dynamik
- D’Alembertsches Prinzip
- Eigenvektor
- Eigenwert
- Eigenwertproblem
- Englisch
- Fehlerquadratsumme
- Finite-Elemente-Methode
- Rayleigh-Ritz-Prinzip
- Finite-Differenzen-Methode
- Floquet-Theorem
- Freischneiden
- Fundamentalmatrix
- Geometrische Zwangsbedingung
- Haften und Reiben
- Hauptspannung
- Innovation
- Kennlinie
- Knotenpunktverfahren
- Koordinaten
- Lagrange-Multiplikator
- Lernvideo
- Mathieusche Differentialgleichung
- Matlab
- Maxima
- Mechatronik
- Modalanalyse
- Newtonverfahren
- Runge-Kutta-Verfahren
- Nichtlineare Schwingungen
- Parametererregte Schwingungen
- Schwingungen von Kontinua
- Smartphone
- Stabilität
- Stabwerk
- Starrer Körper
- Statik
- Stick-Slip-Effekt
- Totzeit