Gelöste Aufgaben/Kw52: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 19: | Zeile 19: | ||
Dies ist eine Näherungslösung zu [[Gelöste Aufgaben/Kw50|Kw50]]. | Dies ist eine Näherungslösung zu [[Gelöste Aufgaben/Kw50|Kw50]]. | ||
</onlyinclude> | </onlyinclude>Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter: | ||
Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter: | |||
<math>\begin{array}{ll}K_C =&\displaystyle 5 \frac{E\,I}{\ell_0}\\m_A =&\displaystyle \frac{m_B}{5} \end{array}</math> | <math>\begin{array}{ll}K_C =&\displaystyle 5 \frac{E\,I}{\ell_0}\\m_A =&\displaystyle \frac{m_B}{5} \end{array}</math> | ||
== Lösung mit Maxima == | |||
Für die Lösung nutzen wir direkt die Elemente aus der [[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]]. | |||
==tmp== | ==tmp== | ||
| Zeile 93: | Zeile 95: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
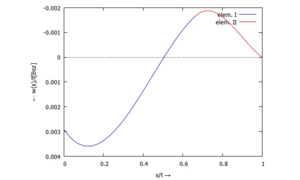
[[Datei:Kw52-11.png|mini|Auslenkung ''w(x)'']] | |||
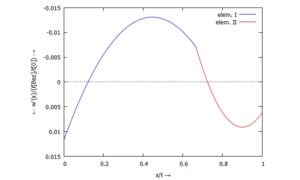
[[Datei:Kw52-12.png|mini|Kippung der Querschnitte ''Φ(x)'']] | |||
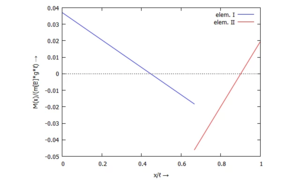
[[Datei:Kw52-13.png|mini|Moment ''M(x)'']] | |||
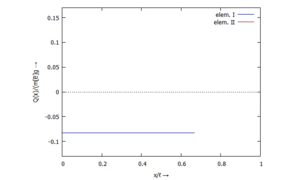
[[Datei:Kw52-14.png|mini|Querkraft ''Q(x)'']] | |||
Version vom 31. März 2021, 05:44 Uhr
Aufgabenstellung
Eine Brücke ABC der Masse mB und homogener Biegesteifigkeit EI ist in C gelenkig gelagert und in A sowie B mit einem Seil verbunden. Das undehnbare Seil wird dabei über eine kleine Rolle (Radius r ≪ ℓ) in D haftungsfrei geführt. In Punkt C ist die Brücke über eine Drehfeder der Steifigkeit KC mit dem Lager verbunden. In A steht eine Person der Masse mA.
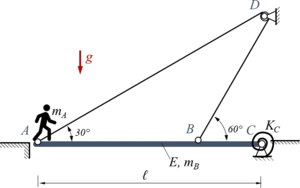
Geben Sie die Lösung für ein Euler-Bernoulli-Modell der Brücke mit dem Ansatz der Finiten Elemente an.
Dies ist eine Näherungslösung zu Kw50. Ermitteln Sie die genäherten Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:
Lösung mit Maxima
Für die Lösung nutzen wir direkt die Elemente aus der FEM-Formulierung für den Euler-Bernoulli-Balken.
tmp
Title
Text
1+1
tmp
Title
Text
1+1
tmp
Title
Text
1+1
tmp
Title
Text
1+1
tmp
Title
Text
1+1
tmp
Title
Text
1+1
tmp
Title
Text
1+1
Links
- Aufgabe Kw50 (analytische Lösung dieser Aufgabe)
- Aufgabe Kw52 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz und Lagrange-Multiplikator)
- Aufgabe Kw53 (Lösung dieser Aufgabe mit dem Ansatz von Rayleigh-Ritz)
Literature
- ...