Gelöste Aufgaben/Kw50: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 11: | Zeile 11: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kw50-01.png|alternativtext=|links|mini|Lageplan]] | ||
Geben Sie die analytische Lösung für ein Euler-Bernoulli-Modell der Brücke in dimensiuonslosen Koordinaten an. | Geben Sie die analytische Lösung für ein Euler-Bernoulli-Modell der Brücke in dimensiuonslosen Koordinaten an. | ||
</onlyinclude> | </onlyinclude> | ||
Ermitteln Sie für dabei die Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter: | |||
<math>\begin{array}{ll}K_C =&\displaystyle 5 \frac{E\,I}{\ell_0}\\m_A =&\displaystyle \frac{m_B}{5} \end{array}</math> | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Die Aufgabe ist ein klassisches Randwertproblem mit | |||
# zwei Gebieten, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast ''q<sub>0</sub>'' belastet ist und somit durch die Differentialbeziehung | |||
<math>E\; I_i w_i^{IV}(x) = q_0,\;\; i=\{1,2\}</math> beschrieben wird; | |||
# Rand- und Übergangsbedingungen in den Punkten A, B, C. | |||
Die Biegesteifigkeit des Balkens ist konstant (nicht von "''x"'' abhängig), wir können als den Index "''i''" beim Flächenmoment also weglassen. | |||
Wir verwenden ein ''x'' bzw. ''ξ'' als Koordinaten in beiden Gebieten, in der Übersicht sieht das Randwertproblem also so aus: | |||
{| class="wikitable" | |||
!'''Rand''' | |||
'''"A"''' | |||
!Bereich I | |||
!'''Übergang''' | |||
'''"B"''' | |||
!Bereich II | |||
!'''Rand''' | |||
'''"C"''' | |||
|- | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|- | |||
| | |||
| | |||
| | |||
| | |||
| | |||
|} | |||
Zusätzlich zum "klassischen" Randwertproblem haben wir hier eine geometrische Zwangsbedingung: Durch die Umlenkrolle ist die vertikale Bewegung in den Punkten ''A'' und ''B'' gekoppelt! | |||
Wie? Das machen wir uns an einem Bild klar:[[Datei:Kw50-12.png|mini|Geometrische Zwangsbedingung|alternativtext=|200x200px]]In linearer Näherung ist der Zusammenhang zwischen der Seil-Abwicklung ''Δs<sub>A</sub>'' und der vertial-Verschibung ''W<sub>A</sub>'' in Punkt ''A'' | |||
<math>\displaystyle \sin(30^\circ) = \frac{\Delta s_A}{W_A}</math>. | |||
Analog gilt für Punkt ''B'' | |||
<math>\displaystyle \sin(60^\circ) = \frac{\Delta s_B}{W_B}</math>. | |||
Da das Seil undehnbar ist, gilt außerdem | |||
<math>\Delta s_A + \Delta s_B = 0</math> | |||
Diese zusätzliche Bedingung ist das entscheidende Element dieser Aufgabe. | |||
==tmp== | ==tmp== | ||
In dieser Lösung arbeiten wir mit dimensionslosen Koordinaten für die unabhängige Koordinate ''x'' und die abhängige Koordinate ''w(x)''. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 29: | Zeile 82: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Streckenlast auf den Balken ist natürlich seine Gewichtskraft, also | ||
<math>\displaystyle q_0 = \frac{m_B\;g}{\ell_0}</math>.[[Datei:Kw50-06.png|mini|Geometrie]]Geometrische Zusammenhänge müssen wir auch anschreiben, so für | |||
<math>\begin{array}{l}\ell = \ell_1 + \ell_2\\\tan(\alpha_B) = \displaystyle \frac{H}{\ell_2}\\\tan(\alpha_A) = \displaystyle \frac{H}{\ell}\end{array}</math> | |||
mit | |||
<math>\alpha_A = 30\circ, \;\;\;\alpha_B = 60\circ</math>. | |||
Und wir wählen noch eine Bezugslänge ''ℓ<sub>Bez</sub>'' zu | |||
<math>\displaystyle \ell_{Bez} = \frac{m_B\;g \ell^3}{3 EI}</math> | |||
aus der tabellierten Lösung für einen Kragbalken der Länge ''ℓ'' und einer Endlast ''m<sub>B</sub> g.'' Das erscheint nicht sonderlich schlau - es gibt Standard -Lastfälle die besser passen würden. Aber dann schleppen wir die ganze Zeit Koeffizienten wie z.B. ''5/384'' mit durch die Rechnungen - das macht die Arbeit unübersichtlich.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 39: | Zeile 107: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung | ||
<math>E\,I\, w_i^{IV}(x) = q_0 ,\;\; i=\{1,2\}</math>, | |||
die wir durch Integration lösen und dann bereichsweise an Rand- und Übergangsbedingungen anpassen. Diese Aufgabe wird etwas übersichtlicher, wenn wir die Auslenkung ''w'' und die Ortskoordinate ''x'' dimensionslos machen. So wählen wir: | |||
<math>w = \ell_{Bez}\cdot \tilde{w}</math> | |||
und setzten für die Bezugslänge die Auslenkung eines Kragbalkens unter konstanter Streckenlast (hier ''q<sub>A</sub>'') an. | |||
Zusätzlich wählen wir eine unabhängige, dimensionslose Ortskoordinaten für die Bereich I und II, die ihren Ursprung in den Punkt A hat: | |||
<math>\xi = \displaystyle \frac{x}{\ell}</math> | |||
Mit den weiteren Gleichungen für | |||
<math>\begin{array}{ll} \ldots\text{ die Verdrehung: }&\displaystyle \phi_i(x) = \frac{d\,w_i(x)}{d\,x}\\ \ldots\text{ das Biege-Moment: }&\displaystyle M_i(x) = - E I \frac{d^2\,w_i(x)}{d\,x^2}\\ \ldots\text{ die Querkraft: }&\displaystyle Q_i(x) = - EI \frac{d^3\,w_i(x)}{d\,x^3} \end{array}</math> | |||
finden wir für Bereich i: | |||
<math>\begin{array}{lll} {{w}_{i}}\left( \xi\right) &:=&\displaystyle \frac{1}{m_B\,g} \left( \frac{1}{8} {q_0}\, {\ell_0}\, {\ell_{Bez}}\, {{\xi}^{4}} + \frac{1}{2} {\ell_0}\, {C_{i,3}}\, {\ell_{Bez}}\, {{\xi}^{3}} + \frac{1}{2} 3 {\ell_0}\, {C_{i,2}}\, {\ell_{Bez}}\, {{\xi}^{2}}+ 3 {\ell_0}\, {C_{i,1}}\, {\ell_{Bez}} \xi\right) + 3 {\ell_0}\, {C_{i,0}}\, {\ell_{Bez}}\\ \phi_{i}\left( \xi\right) &:=&\displaystyle \frac{1}{m_B\,g} \left(\frac{1}{2} {{q}_{0}}\cdot \ell_{Bez}\cdot {{\xi}^{3}} + \frac{1}{2} 3\cdot {{C}_{i,3}}\cdot \ell_{Bez}\cdot {{\xi}^{2}} + 3\cdot {{C}_{i,2}}\cdot \ell_{Bez}\cdot \xi + 3\cdot {{C}_{i,1}}\cdot \ell_{Bez} \right)\\ {{M}_{i}}\left( \xi\right) &:=&\displaystyle \frac{E I}{2 \ell_0 m_B\,g} \left(-3\cdot {{q}_{0}}\cdot \ell_{Bez}\cdot {{\xi}^{2}}-6\cdot {{C}_{i,3}}\cdot \ell_{Bez}\cdot \xi-6\cdot {{C}_{i,2}}\cdot \ell_{Bez} \right)\\ {{Q}_{i}}\left( \xi\right) &:=&\displaystyle \frac{E I}{\ell_0^2 m_B\,g} \left(-3\cdot {{q}_{0}}\cdot \ell_{Bez}\cdot \xi-3\cdot {{C}_{i,3}}\cdot \ell_{Bez} \right) \end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Integration Of Differential Equation | {{MyCodeBlock|title=Integration Of Differential Equation | ||
|text=Text | |text=Text | ||
| Zeile 49: | Zeile 138: | ||
==tmp== | ==tmp== | ||
Für die 2*4 = 8 Integrationskonstanten | |||
<math>\left[ C_{1,0},C_{1,1},C_{1,2},C_{1,3},C_{2,0},C_{2,1},C_{2,2},C_{2,3}\right]</math> | |||
suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen. Und zusätzlich - und das ist hier besonders - brauchen wir noch eine Gleichung für die Seilkraft ''S''. | |||
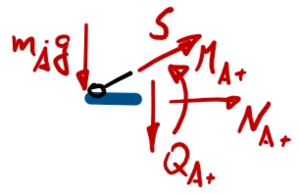
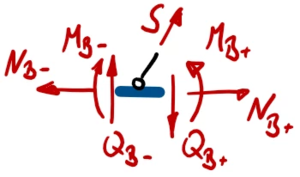
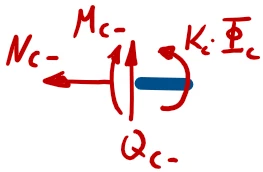
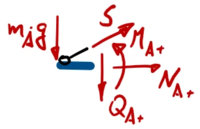
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten ''A, B, C'' und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen. | |||
Die Normalkräfte ''N'' brauchen wir dabei nicht auszuwerten. | |||
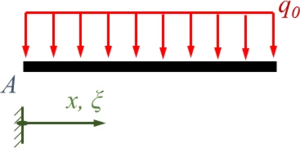
===== Aus Rand A: ===== | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Boundary Conditions | {{MyCodeBlock|title=Boundary Conditions | ||
|text=Text | |text=Text | ||
| Zeile 89: | Zeile 191: | ||
<table class="wikitable" style="background-color:white; float: left; margin-right:14px;"> | <table class="wikitable" style="background-color:white; float: left; margin-right:14px;"> | ||
<tr>< | <tr><td>[[Datei:Kw50-11A.png|rahmenlos|alternativtext=|200x200px]] | ||
< | </td><td>Geometrische Randbedingungen | ||
* keine | |||
Kraft- und Momenten-Randbedingungen | |||
# <math>m_A\;g - S \sin(\alpha_A) + Q_{A,+}= 0 \text{ mit } Q_{A,+} = - E I\cdot w'''(x)|_{x=0}</math> | |||
# <math>M_{A,+}= 0 \text{ mit } M_{A,+} = - E I\cdot w'''(x)|_{x=0}</math> | |||
</td></tr> | |||
</table> | </table> | ||
[[Datei:Kw50-11A.png|rahmenlos]][[Datei:Kw50-11AB.png|rahmenlos]][[Datei:Kw50-11B.png|rahmenlos]][[Datei:Kw50-11BC.png|rahmenlos]][[Datei:Kw50-11C.png|rahmenlos]] | [[Datei:Kw50-11A.png|rahmenlos]][[Datei:Kw50-11AB.png|rahmenlos]][[Datei:Kw50-11B.png|rahmenlos]][[Datei:Kw50-11BC.png|rahmenlos]][[Datei:Kw50-11C.png|rahmenlos]] | ||
Version vom 29. März 2021, 13:47 Uhr
Aufgabenstellung
Eine Brücke ABC der Masse mB und homogener Biegesteifigkeit EI ist in C gelenkig gelagert und in A sowie B mit einem Seil verbunden. Das undehnbare Seil wird dabei über eine kleine Rolle (Radius r ≪ ℓ) in D haftungsfrei geführt. In Punkt C ist die Brücke über eine Drehfeder der Steifigkeit KC mit dem Lager verbunden. In A steht eine Person der Masse mA.
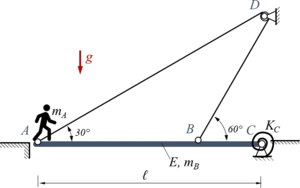
Geben Sie die analytische Lösung für ein Euler-Bernoulli-Modell der Brücke in dimensiuonslosen Koordinaten an.
Ermitteln Sie für dabei die Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:
Lösung mit Maxima
Die Aufgabe ist ein klassisches Randwertproblem mit
- zwei Gebieten, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast q0 belastet ist und somit durch die Differentialbeziehung
beschrieben wird;
- Rand- und Übergangsbedingungen in den Punkten A, B, C.
Die Biegesteifigkeit des Balkens ist konstant (nicht von "x" abhängig), wir können als den Index "i" beim Flächenmoment also weglassen.
Wir verwenden ein x bzw. ξ als Koordinaten in beiden Gebieten, in der Übersicht sieht das Randwertproblem also so aus:
| Rand
"A" |
Bereich I | Übergang
"B" |
Bereich II | Rand
"C" |
|---|---|---|---|---|
Zusätzlich zum "klassischen" Randwertproblem haben wir hier eine geometrische Zwangsbedingung: Durch die Umlenkrolle ist die vertikale Bewegung in den Punkten A und B gekoppelt!
Wie? Das machen wir uns an einem Bild klar:
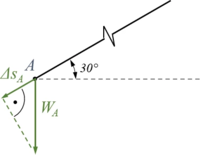
In linearer Näherung ist der Zusammenhang zwischen der Seil-Abwicklung ΔsA und der vertial-Verschibung WA in Punkt A
.
Analog gilt für Punkt B
.
Da das Seil undehnbar ist, gilt außerdem
Diese zusätzliche Bedingung ist das entscheidende Element dieser Aufgabe.
tmp
In dieser Lösung arbeiten wir mit dimensionslosen Koordinaten für die unabhängige Koordinate x und die abhängige Koordinate w(x).
Header
Text
1+1
tmp
Die Streckenlast auf den Balken ist natürlich seine Gewichtskraft, also
.
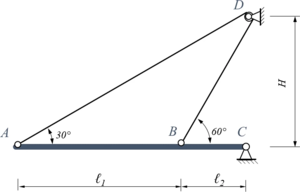
Geometrische Zusammenhänge müssen wir auch anschreiben, so für
mit
.
Und wir wählen noch eine Bezugslänge ℓBez zu
aus der tabellierten Lösung für einen Kragbalken der Länge ℓ und einer Endlast mB g. Das erscheint nicht sonderlich schlau - es gibt Standard -Lastfälle die besser passen würden. Aber dann schleppen wir die ganze Zeit Koeffizienten wie z.B. 5/384 mit durch die Rechnungen - das macht die Arbeit unübersichtlich.
Declarations
Text
1+1
tmp
In Bereich I und II gilt dieselbe Bewegungs-Differentialgleichung
,
die wir durch Integration lösen und dann bereichsweise an Rand- und Übergangsbedingungen anpassen. Diese Aufgabe wird etwas übersichtlicher, wenn wir die Auslenkung w und die Ortskoordinate x dimensionslos machen. So wählen wir:
und setzten für die Bezugslänge die Auslenkung eines Kragbalkens unter konstanter Streckenlast (hier qA) an.
Zusätzlich wählen wir eine unabhängige, dimensionslose Ortskoordinaten für die Bereich I und II, die ihren Ursprung in den Punkt A hat:
Mit den weiteren Gleichungen für
finden wir für Bereich i:
.
Integration Of Differential Equation
Text
1+1
tmp
Für die 2*4 = 8 Integrationskonstanten
suchen wir jetzt die passenden Gleichungen aus Rand- und Übergangsbedingungen. Und zusätzlich - und das ist hier besonders - brauchen wir noch eine Gleichung für die Seilkraft S.
Zur besseren Übersicht nennen wir die Schnitt-Momente und -Kräfte nach den jeweiligen Knotenpunkten A, B, C und fügen als Index ein + / - hinzu, um die Seite (+: rechts vom Knoten, -: links vom Knoten) zu kennzeichnen.
Die Normalkräfte N brauchen wir dabei nicht auszuwerten.
Aus Rand A:
Boundary Conditions
Text
1+1
tmp
Prepare for Solver
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1
| Geometrische Randbedingungen
Kraft- und Momenten-Randbedingungen |
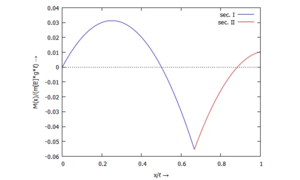
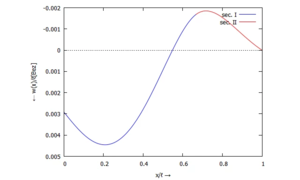
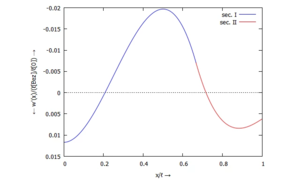
Links
- ...
Literature
- ...