Gelöste Aufgaben/Kw30

Aufgabenstellung

Manchmal stößt man in unscheinbaren Aufgabenstellungen auf unerwartete Hindernisse - so in dieser Aufgabe eines mathematischen Pendels, die auf eine Bewegungsgleichung mit periodischen Koeffizienten führt.

Lageplan

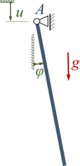
Das Pendel der Masse m und Länge ℓ der Aufgabe hat einen in A senkrecht mit u(t) periodisch bewegten Aufhängepunkt.

Berechnen Sie die Stabilität der Lösung der linearisierten Bewegungsgleichung für verschiedene Parameterkombinationen.

Gegeben sind

• m, ℓ, g sowie
• $u(t)={\hat {u}}\cdot \cos(\Omega \;t)$

Lösung mit Maxima

Equations of Motion

Koordinaten und Freikörperbild

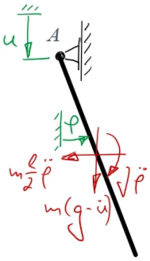
Aus dem Freikörperbild erhalten wir die Bewegungsgleichung

$\displaystyle J{\ddot {\varphi }}+{\frac {\ell }{2}}\;m\;{\frac {\ell }{2}}\;{\ddot {\varphi }}+m\;(g-{\ddot {u}})\;\sin(\varphi )=0$

mit

$\displaystyle {\dot {(.)}}:={\frac {d}{dt}}(.)$.

Wir linearisieren und erhalten mit

$\displaystyle \sin(\varphi )\approx \varphi ,\;\;J={\frac {m\;\ell ^{2}}{12}}$

die lineare Differentialgleichung mit perdiodischen Koeffizienten

$\displaystyle {\frac {1}{3}}m\cdot {{\ell }^{2}}\cdot {\ddot {\varphi }}+m\cdot \ell \cdot \left(g+\Omega ^{2}\;{\hat {u}}\;\cos(\Omega \;t)\right)\cdot \varphi =0$.

Das ist eine Grundform der Mathieuschen Differentialgleichung - die wir noch in dimensionslose Form bringen wollen. Dazu soll die zugeordnete gewöhnliche Differentialgleichung mit konstanten Koeffizienten, also für

${\hat {u}}=0$,

in dimensionsloser Schreibweise und für einfache Parameter-Konstellationen die Periodendauer "1" haben. Das erreichen mit der dimensionslosen Zeit

$\displaystyle t=T\cdot \tau {\text{ und }}\Omega ={\frac {2\pi }{T}}$

und den dimensionslosen Parametern

$\displaystyle \Lambda ={\frac {3\;g}{\Omega ^{2}\;\ell }}{\text{ und }}\Gamma ={\frac {3\;U}{\ell }}$.

Damit ist

$\displaystyle \varphi ''+(2\pi )^{2}\cdot \left(\Lambda +\Gamma \cdot \cos(2\pi \;\tau )\right)\cdot \varphi =0{\text{ mit }}(.)':={\frac {d}{d\tau }}(.)$.

Für Λ=1 ist das wie gewünscht eine Bewegungsgleichung mit der Periodendauer "1":

$\varphi ''+(2\pi )^{2}\;\varphi =0$.

/*********************************************************/
/* MAXIMA script                                         */
/* version: wxMaxima 15.08.2                             */
/* author: Andreas Baumgart                              */
/* last updated: 2018-12-30                              */
/* ref: Kw30                                             */
/* description: finds the solution for                   */
/*              Mathieus Differential Equation           */
/*********************************************************/
 
/*********************************************************/
declare("ℓ", alphabetic);
load(eigen)$
/*load (lapack)$*/

/* declare parameters */
params: [J=m*ℓ^2/12, Omega=2*%pi/T, Lambda = (3*g)/(Omega^2*ℓ), Gamma = (3*U)/ℓ];

/*********************************************************/
/* equations of motion                                   */
eom: J*'diff(phi,t,2) + ℓ/2*m*ℓ/2*'diff(phi,t,2)*cos(phi) + m*(g-'diff(u,t,2))*ℓ*sin(phi) = 0;
linearize : [sin(phi) = phi, cos(phi) = 1];
eom : subst(params,subst(linearize,eom));

eom : subst(['diff(phi,t,2) = 'diff(p,tau,2)/T^2,subst(params,'diff(u,t,2) = diff(U*cos(Omega*t),t,2)), t=T*tau],eom);
eom : expand(subst(solve(rest(params, 1),[T,g,U]),eom*12*%pi^2/m/ℓ^2/Omega^2));
eom : ['diff(p,t) = v,
'diff(v,t) = subst([phi=p,tau=t],subst(solve(eom, 'diff(p,tau,2))[1],'diff(p,tau,2)))];

Solve and Check for Stability of Solution

Für die Stabilität der Bewegungsgleichung brauchen wir den Satz von Floquet-Ljapunow und die Fundamentalmatrix Φ. Zunächst schreiben wir die Bewegungsgleichung als Differentialgleichung erster Ordnung  als

${\underline {q}}'=\left({\begin{array}{c}\psi \\-(2\pi )^{2}\cdot \left(\Lambda +\Gamma \cdot \cos(2\pi \;\tau )\right)\cdot \varphi \end{array}}\right){\text{ mit }}{\underline {q}}=\left({\begin{array}{c}\varphi \\\psi \end{array}}\right)$

bzw. als

${\underline {q}}'=\underbrace {\left({\begin{array}{c}0&1\\-(2\pi )^{2}\cdot \left(\Lambda +\Gamma \cdot \cos(2\pi \;\tau )\right)&0\end{array}}\right)} _{\displaystyle :={\underline {\underline {A(\tau )}}}}\cdot {\underline {q}}$.

Durch den Zeit-periodischen Koeffizienten in τ hat diese Bewegungsgleichung keine "einfachen" Lösungen der Form e^λt mehr. Statt dessen untersuchen wir die Stabilität anhand der Fundamentalmatrix Φ^*, in der zwei Fundamentalösungen

${\underline {\underline {\Phi }}}:=\left({\underline {q}}_{T,1},{\underline {q}}_{T,2}\right)$

mit

${\underline {q}}_{T,1}={\underline {q}}_{1}(T){\text{und }}{\underline {q}}_{1}(0)=\left({\begin{array}{c}1\\0\end{array}}\right)$

und

${\underline {q}}_{T,2}={\underline {q}}_{2}(T){\text{und }}{\underline {q}}_{2}(0)=\left({\begin{array}{c}0\\1\end{array}}\right)$

stehen.

Abbildungsvorschrift über die Periodendauer.

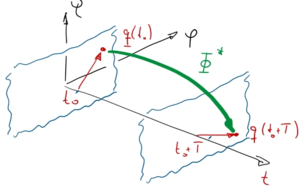
Wir interpretieren also die Fundamentalmatrix Φ^* als Abbildungsvorschrift, um die Anfangsbedingungen q(0)  über das Zeitintervall - hier T = 1 - hinweg abzubilden.

Die Eigenwerte μ_i der Fundamentalmatrix heißen

• charakteristische Multiplikatoren.

Die charakteristischen Exponenten sind

• $\varrho _{i}=\ln(\mu _{i})$.

Damit Lösungen der Bewegungsgleichung stabil sind, muss

$|\mu _{i}|<1{\text{ bzw. }}\Re (\varrho _{i})<0$

für alle Eigenwerte gelten. Die Fudnamentalmatrix erhalten wir am besten durch die numerische Lösung der Bewegungsgleichung als Anfangswertproblem - hier mit dem Runge-Kutta-Verfahren 4.ter Ordnung - z.B. für

$\Lambda =1,\;\;\Gamma =1.$

Durch zweifache Lösung des Anfangswertproblems finden wir

${\underline {\underline {\Phi }}}^{*}={\begin{pmatrix}0.024&1.168\\1.168&15.035\end{pmatrix}}$.

Die Fundamentalmatrix hat die Eigenwerte

${\begin{array}{l}\mu _{1}=-0.0661,\\\mu _{2}=15.1256\end{array}}$

und besitzt damit einen Eigenwert, dessen Betrag größer als "1" ist - die Lösung ist instabil.

Instabile Lösung

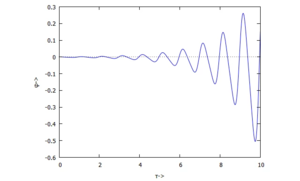
Das können wir prüfen, indem wir uns die numerische Lösung im Zeitbereich anschauen:

• der Winkel der Auslenkung wächst (exponentiell) mit der Zeit.

/*********************************************************/
/* numerical solution of IVP                             */
numpars: [Lambda = [-1,2], Gamma   = [0,3]];
times : subst([t0 = 0, tmax = 1, dt = 0.01],
                    [t, t0, tmax, dt]);
runs : [30,30];
stateVabs : [p,v];
initiVals : [[0,1],[1,0]];
for p1: 0 thru runs[1] do
  (for p2: 0 thru runs[2] do
      (print("step ",p1," - ", p2),
       pars: [Lambda = subst(numpars, Lambda)[1]+(subst(numpars, Lambda)[2]-subst(numpars, Lambda)[1])*p1/runs[1],
              Gamma  = subst(numpars, Gamma )[1]+(subst(numpars, Gamma )[2]-subst(numpars, Gamma )[1])*p2/runs[2]],
       dgl1stOrder : float(subst(pars,[rhs(eom[1]),rhs(eom[2])])),
       Phi : [],
       for i:1 thru 2 do
          (ivs : rk(dgl1stOrder, stateVabs, initiVals[i], times),
           Phi : append(Phi,[rest (ivs[length(ivs)], 1)])),
       Phi : funmake('matrix,Phi),
       mu[p1+1,p2+1] : lmax(abs(float(eigenvalues(Phi)[1])))))$

Ince-Struttsche Karte

Diese Untersuchung können wir nun für eine Reihe von Parameter-Konstellationen wiederholen und den größeren der beiden charakteristischen Exponenten jeweils auftragen.

Stabilitätskarte

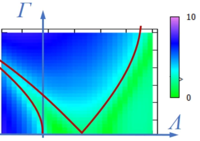
Wir untersuchen den Bereich

$\Lambda =-1\ldots 2,\;\;\Gamma =0\ldots 3.$

und tragen die Werte des Exponenten ρ farbig kodiert auf:

Bei genauerer Analyse können wir die stabilen (grün) von den instabilen Parameter-Bereichen durch eine rote Linie trennen.

Dies ist ein Ausschnitt der Ince-Struttschen Karte. Sie gibt die Stabilität der Lösungen der Mathieuschen Differentialgleichungen an.

Ince-Struttsche Karte

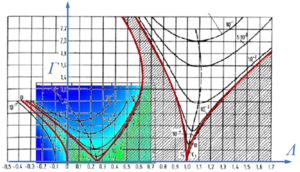
Und so sieht die gesamte Ince-Struttsche Karte aus:

Achtung: hier wurden unterschiedliche Parameterwerte für Λ und Γ verwendet!

Wir erkennen: bei periodischer Erregung des Fußpunktes hat

• das gewöhnliche mathematische Pendel (Λ>0) große Bereiche dynamischer Instabilität!
• das inverse Pendel (Λ<0) Bereiche dynamischer Stabilität!

---

Links

• https://youtu.be/rwGAzy0noU0

Literature

• ...