Gelöste Aufgaben/Kw30: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
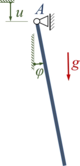
Lageplan
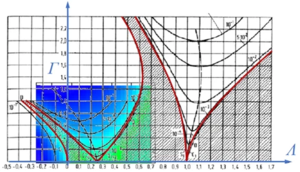
Ince-Struttsche Karte 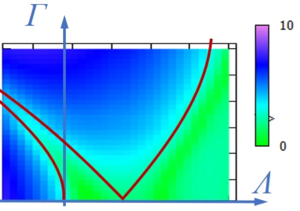
Stabilitätskarte 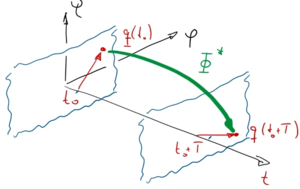
Abbildungsvorschrift 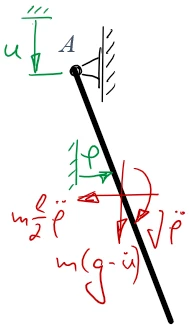
Koordinaten und Freikörperbild 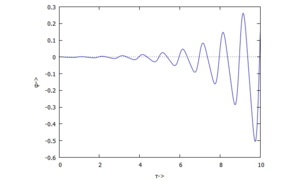
Instabile Lösung 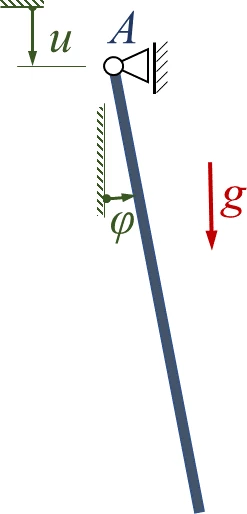
Lageplan
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 58: | Zeile 58: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Oft stößt man in unscheinbaren Aufgabenstellungen auf unerwartete Hindernisse - so in dieser Aufgabe eines mathematischen Pendels, die auf eine Bewegungsgleichung mit periodischen Koeffizienten führt. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kw30-01.png|alternativtext=|links|mini|166x166px|Lageplan]] | ||
Das Pendel der Masse ''m'' und Länge ''ℓ'' der Aufgabe hat einen in ''A'' senkrecht mit ''u(t)'' periodisch bewegten Aufhängepunkt. | |||
Berechnen Sie die Stabilität der Lösung der linearisierten Bewegungsgleichung für verschiedene Parameterkombinationen. | |||
</onlyinclude> | </onlyinclude> | ||
Gegeben sind | |||
* ''m, ℓ, g'' sowie | |||
* <math>u(t) = \hat{u} \cdot \cos(\Omega\;t)</math> | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
==tmp== | ==tmp== | ||
Version vom 29. März 2021, 11:40 Uhr
Aufgabenstellung
Oft stößt man in unscheinbaren Aufgabenstellungen auf unerwartete Hindernisse - so in dieser Aufgabe eines mathematischen Pendels, die auf eine Bewegungsgleichung mit periodischen Koeffizienten führt.

Das Pendel der Masse m und Länge ℓ der Aufgabe hat einen in A senkrecht mit u(t) periodisch bewegten Aufhängepunkt.
Berechnen Sie die Stabilität der Lösung der linearisierten Bewegungsgleichung für verschiedene Parameterkombinationen.
Gegeben sind
- m, ℓ, g sowie
Lösung mit Maxima
tmp
Equations of Motion
Text
1+1
tmp
Solve and Check for Stability of Solution
Text
1+1
tmp
Ince-Struttsche Karte
Text
1+1






Links
Literature
- ...
Kategorien:
- Gelöste Aufgaben
- Dimensionslose Schreibweise
- A*x=b
- Lineare Algebra
- Achsensymmetrie
- Rotationssymmetrie
- Analytische Lösung
- Numerische Lösung
- Anfangswertproblem
- Randwertproblem
- Ansys
- Shell-Element
- Arbeitsfunktion
- Potential
- Prinzip der virtuellen Arbeit
- Prinzip der virtuellen Verrückungen
- Prinzip vom Minimum der Potentiellen Energie
- Formänderungsenergie
- Axiom
- Biege-Belastung
- Membranspannung
- Computer
- Stab
- Dehnstab
- Euler-Bernoulli-Balken
- Timoshenko-Balken
- Feder-Masse-System
- Draft
- Dynamik
- D’Alembertsches Prinzip
- Eigenvektor
- Eigenwert
- Eigenwertproblem
- Englisch
- Fehlerquadratsumme
- Finite-Elemente-Methode
- Rayleigh-Ritz-Prinzip
- Finite-Differenzen-Methode
- Floquet-Theorem
- Freischneiden
- Fundamentalmatrix
- Geometrische Zwangsbedingung
- Haften und Reiben
- Hauptspannung
- Innovation
- Kennlinie
- Knotenpunktverfahren
- Koordinaten
- Lagrange-Multiplikator
- Lernvideo
- Mathieusche Differentialgleichung
- Matlab
- Maxima
- Mechatronik
- Modalanalyse
- Newtonverfahren
- Runge-Kutta-Verfahren
- Nichtlineare Schwingungen
- Parametererregte Schwingungen
- Schwingungen von Kontinua
- Smartphone
- Stabilität
- Stabwerk
- Starrer Körper
- Statik
- Stick-Slip-Effekt
- Totzeit