Gelöste Aufgaben/Kw28: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 12: | Zeile 12: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Das System besteht aus einer Kugel (Radius ''r'', Masse ''m<sub>2</sub>'') und einer Plattform (Masse ''m<sub>1</sub>''). Wie skizziert ist die Plattform mit einer Parallelführung aus zwei Euler-Bernoulli-Balken (Biegesteifigkeit ''EI'') elastisch gelagert. Aus der statischen Referenzkonfiguration wird die Kugel aus der Höhe H über der Plattform losgelassen. Kugel und Plattform stoßen also aufeinander und führen dann Ihre eigene vertikale Bewegung durch - bis zur nächsten Kollision. Der Stoß zwischen Kugel und Oberfläche sei ideal-elastisch. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kw28-01.png|alternativtext=|links|mini|Lageplan]] | ||
Gesucht ist | Für das skizzierte System modellieren Sie die Kugel als elastisch, die elastisch gelagerte Plattform als starr. | ||
Gesucht ist eine numerische Lösung als Anfangswertproblem und die nichtlinearen Schwingungen der beiden Systemteile. | |||
</onlyinclude> | </onlyinclude> | ||
| Zeile 24: | Zeile 25: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Kugel können Sie sich im unteren Teil durch eine Feder der Steifigkeit ''k<sub>2</sub>'' ersetzt denken - das geht analog zu Beispiel [[Gelöste Aufgaben/Kw23|Kw23]]. | ||
Die Federkraft ''K'' ist also Null, solange die Kugel die Oberfläche nicht berührt und sie ist proportional zur Federkompression ''w'', wenn sich Kugel und Oberfläche berühren. | |||
Die beiden Körper haben jeweils einen Freiheitsgrad in vertikale Richtung. Die Bewegungsgleichungen für die beiden Körper sind stückweise linear (Kontakt: ''K = k w'' / kein Kontakt ''K = 0''). Den Kontakt erfassen wir durch eine Kennlinie, die wir zwischen den beiden linearen Bereichen ausrunden. Das Ausrunden macht die numerische Integration schneller. | |||
Wir lösen das Anfangswertproblem zu der zugeordneten nichtlinearen Bewegungsgleichung. Die Nichtlinearität kommt hier aus der Kontaktbedingung zwischen der Kugel und der Plattform..<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 35: | Zeile 47: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Koordinaten der Verschiebung der beiden Massen nennen wir | ||
<math>\underline{Q}(t)=\left(\begin{array}{l}u_1(t)\\u_2(t)\end{array}\right) \text{ und damit }\delta \underline{Q}=\left(\begin{array}{l}\delta u_1\\\delta u_2\end{array}\right)</math>. | |||
Für die beiden elastischen Balken verwenden die [[Sources/Lexikon/Ersatzfeder-Steifigkeit|Ersatzfeder-Steifigkeit]] | |||
<math>\displaystyle k_1 =\displaystyle 2\cdot\frac{12 EI}{\ell^3}</math>. | |||
Und als Abkürzungen verwenden wir | |||
<math>\begin{array}{ll}\alpha &= \displaystyle \frac{m_2}{m_1}\\\kappa &=\displaystyle \frac{k_2}{k_1}\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 46: | Zeile 70: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Kennlinie für den Kontakt definieren wir stückweise zu | ||
<math>K(w,\epsilon) = k\cdot \left\{ \begin{array}{ccl} 0 &\text{für}& \;\;\;\;\;\;\;\;w < -\epsilon\\\displaystyle \frac{1}{4} \left( 1+\frac{w}{\epsilon}\right)^2 &\text{für}& -\epsilon < w < +\epsilon\\ w &\text{für}& +\epsilon < w\\ \end{array} \right.</math> | |||
[[Datei:Kw28-13.png|mini|Kontakt-Kennlinie]]Und so sieht die Kennlinie dann aus: | |||
Die Parabel zwischen den beiden linearen Kennlinien-Stücken macht die Kraft ''K'' stetig differentierbar in ''w''. Das macht die numerische Integration schneller - und genauer.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Contact Characteristic | {{MyCodeBlock|title=Contact Characteristic | ||
|text=Text | |text=Text | ||
| Zeile 57: | Zeile 87: | ||
==tmp== | ==tmp== | ||
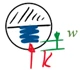
<!--------------------------------------------------------------------------------> | [[Datei:Kw28-10.png|mini|Koordinaten|alternativtext=|250x250px]]Die Gleichgewichtsbedingung konstruieren wir mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] - wir brauchen also kein [[Sources/Lexikon/Freikörperbild|Freikörperbild]]. | ||
Dazu verwenden wir die Verschiebungs-Koordinaten ''u<sub>1</sub>, u<sub>2</sub>'' der beiden Körper wie skizziert. | |||
Für die allgemeine Gleichgewichtsbedingung | |||
<math>\begin{array}{ll}\delta W &= 0\\&= \delta W^a - \delta \Pi\end{array}</math> | |||
setzen wir für die virtuelle Arbeit von äußeren, eingeprägte Kräften (inklusive der [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'sche Trägheitskraft]]) an: | |||
<math>\displaystyle \delta W^a = -\sum_{i=1}^2 m_i\cdot\left(\ddot{u}_i+g\right) \cdot \delta u_i</math> | |||
sowie für die virtuelle Formänderungsenergie der beiden Ersatz-Federn: | |||
<math>\delta \Pi = k_1 u_1(t) \cdot \delta u_1 + \underbrace{K(u_1(t)-u_2(t))}_{\displaystyle \text{Kontakt-Kraft}}\cdot (\delta u_1-\delta u_2)</math>. | |||
Sortieren nach den virtuellen Verrückungen und anschrieben der Gleichgewichtsbedingungen in Matrix-Form liefert | |||
<math>\begin{pmatrix}{{m}_{1}} & 0\\ 0 & {{m}_{2}}\end{pmatrix} \cdot \begin{pmatrix}{\ddot{u}_{1}} \\ {\ddot{u}_{2}} \end{pmatrix} + \begin{pmatrix}{{k}_{1}} & 0\\ 0 & 0\end{pmatrix} \cdot \begin{pmatrix}{{u}_{1}} \\ {{u}_{2}} \end{pmatrix} = -g\cdot \begin{pmatrix}{{m}_{1}}\\ {{m}_{2}}\end{pmatrix} + K\left(u_1 - u_2\right) \cdot \begin{pmatrix}-1 \\ +1 \end{pmatrix}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text=Text | |text=Text | ||
| Zeile 68: | Zeile 117: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Mit einer passenden Bezugszeit und -länge machen wir die Bewegungsgleichungen dimensionslos. | ||
Hier liefert die Periodendauer der Plattform - allein, ohne Kugel - die Bezugszeit ''T''. Die statische Absenkung der Plattform - ohne Einfluss der Kugel - liefert die Bezugslänge ''L''. | |||
Aus der Bewegungsgleichung oben lesen wir für ''K(u<sub>1</sub>-u<sub>2</sub>) = 0'' ab: | |||
<math>T= \displaystyle \frac{2\pi}{\omega_0} \text{ mit } \omega_0^2= \displaystyle \frac{k_1}{m_1}</math> | |||
und | |||
<math>L=\displaystyle \frac{m_1}{k_1} g</math>. | |||
Nun ist also | |||
<math>\displaystyle \tau = \frac{t}{T} \text{ mit } (.)':=\frac{d}{d\tau}(.)</math> | |||
und | |||
<math>\displaystyle U_i = \frac{u_i}{L} \text{ für } i=1,2</math> | |||
Die Kennlinie überführen wir entsprechend in | |||
<math>K(w) = k_2\cdot L\cdot C\left(\displaystyle \frac{W}{\epsilon}\right) \text{ mit } W(\tau) = U_1-U_2 </math>. | |||
Einsetzen liefert die zwei Differentialgleichungen | |||
<math>\begin{array}{llll}\displaystyle \frac{1 }{4\cdot \pi^2 }U''_1 \left( \tau\right)&+{{U}_{1}}\left( \tau\right) &+1&=-\kappa\cdot C\left( \frac{W}{\epsilon}\right) \\\displaystyle \frac{\alpha}{4\cdot \pi^2 }U''_2 \left( \tau\right)& &+\alpha&=+\kappa\cdot C\left( \frac{W}{\epsilon}\right) \end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Dimensionless Equations of Motion | {{MyCodeBlock|title=Dimensionless Equations of Motion | ||
|text=Text | |text=Text | ||
| Zeile 79: | Zeile 155: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Für die numerische Lösung schreiben wir die zwei Bewegungsgleichung zweiter Ordnung um als vier Bewegungsgleichungen erster Ordnung zu | ||
<math>\displaystyle \frac{d}{d\,\tau}\left(\begin{array}{c}U_1\\U_2\\V_1\\V_2\end{array}\right) = \underline{f}(U_1,U_2) \text{ mit } V_i = \frac{d U_i}{d\,\tau}</math>. | |||
Die rechte Seite der gewöhnlichen Differentialgleichung ("Right-hand-side of ODE") lautet damit | |||
<math>\underline{f} = \left(\begin{array}{c}1\\1\\\displaystyle 4\pi^2 (-U_1-1-\kappa\cdot C \cdot \left( \frac{W}{\epsilon}\right))\\\displaystyle 4\pi^2 (-1+\frac{\kappa\cdot C}{\alpha} \cdot \left( \frac{W}{\epsilon}\right))\end{array}\right)</math> | |||
Die dimensionslosen Parameter wählen wir zu | |||
<math>\displaystyle \kappa=10,\alpha=\frac{1}{2},\epsilon=\frac{1}{100}</math> | |||
und lösen die Bewegungsgleichungen numerisch - hier mit dem [[Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Runge-Kutta-Verfahren 4.ter Ordnung|Runge-Kutta-Verfahren 4.ter Ordnung]].<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 89: | Zeile 178: | ||
==tmp== | ==tmp== | ||
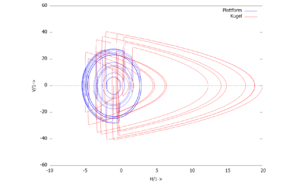
Als Lösung tragen wir die Zeitverläufe der Höhen ''U<sub>1</sub>, U<sub>2</sub>'' über der Zeit ''τ'' | |||
[[Datei:Kw28-21.png|mini|Zeitverlauf der Lösung|alternativtext=|ohne]]und ''U<sub>1</sub>, U<sub>2</sub>'' jeweils über ''V<sub>1</sub>, V<sub>2</sub>'' im Phasendiagramm auf: | |||
[[Datei:Kw28-22.png|mini|Phasendiagramm|alternativtext=|ohne]] | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
| Zeile 100: | Zeile 193: | ||
<table class="wikitable" style="background-color:white; float: left; margin-right:14px;"> | <table class="wikitable" style="background-color:white; float: left; margin-right:14px;"> | ||
<tr><td>[[Datei:Kw28-11.png|rahmenlos|80x80px]] | <tr><td colspan="2">''Kugel-Modell:'' | ||
''elast. Kontakt mit Einfederung w.'' | |||
</td></tr><tr><td>[[Datei:Kw28-11.png|rahmenlos|80x80px]] | |||
| Zeile 106: | Zeile 201: | ||
</td></tr> | </td></tr> | ||
</table> | </table> | ||
<hr/> | <hr/> | ||
Version vom 29. März 2021, 10:55 Uhr
Aufgabenstellung
Das System besteht aus einer Kugel (Radius r, Masse m2) und einer Plattform (Masse m1). Wie skizziert ist die Plattform mit einer Parallelführung aus zwei Euler-Bernoulli-Balken (Biegesteifigkeit EI) elastisch gelagert. Aus der statischen Referenzkonfiguration wird die Kugel aus der Höhe H über der Plattform losgelassen. Kugel und Plattform stoßen also aufeinander und führen dann Ihre eigene vertikale Bewegung durch - bis zur nächsten Kollision. Der Stoß zwischen Kugel und Oberfläche sei ideal-elastisch.
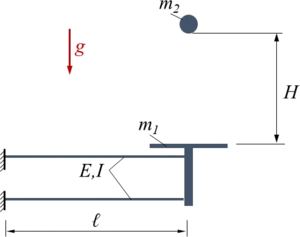
Für das skizzierte System modellieren Sie die Kugel als elastisch, die elastisch gelagerte Plattform als starr. Gesucht ist eine numerische Lösung als Anfangswertproblem und die nichtlinearen Schwingungen der beiden Systemteile.
Lösung mit Maxima
Lorem Ipsum ....
tmp
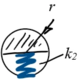
Die Kugel können Sie sich im unteren Teil durch eine Feder der Steifigkeit k2 ersetzt denken - das geht analog zu Beispiel Kw23.
Die Federkraft K ist also Null, solange die Kugel die Oberfläche nicht berührt und sie ist proportional zur Federkompression w, wenn sich Kugel und Oberfläche berühren.
Die beiden Körper haben jeweils einen Freiheitsgrad in vertikale Richtung. Die Bewegungsgleichungen für die beiden Körper sind stückweise linear (Kontakt: K = k w / kein Kontakt K = 0). Den Kontakt erfassen wir durch eine Kennlinie, die wir zwischen den beiden linearen Bereichen ausrunden. Das Ausrunden macht die numerische Integration schneller.
Wir lösen das Anfangswertproblem zu der zugeordneten nichtlinearen Bewegungsgleichung. Die Nichtlinearität kommt hier aus der Kontaktbedingung zwischen der Kugel und der Plattform..
Header
Text
1+1
tmp
Die Koordinaten der Verschiebung der beiden Massen nennen wir
.
Für die beiden elastischen Balken verwenden die Ersatzfeder-Steifigkeit
.
Und als Abkürzungen verwenden wir
.
Declarations
Text
1+1
tmp
Die Kennlinie für den Kontakt definieren wir stückweise zu
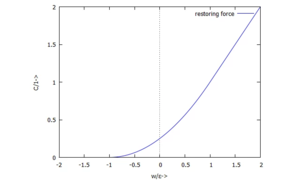
Und so sieht die Kennlinie dann aus:
Die Parabel zwischen den beiden linearen Kennlinien-Stücken macht die Kraft K stetig differentierbar in w. Das macht die numerische Integration schneller - und genauer.
Contact Characteristic
Text
1+1
tmp
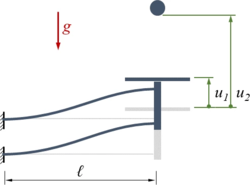
Die Gleichgewichtsbedingung konstruieren wir mit dem Prinzip der virtuellen Verrückungen - wir brauchen also kein Freikörperbild.
Dazu verwenden wir die Verschiebungs-Koordinaten u1, u2 der beiden Körper wie skizziert.
Für die allgemeine Gleichgewichtsbedingung
setzen wir für die virtuelle Arbeit von äußeren, eingeprägte Kräften (inklusive der D'Alembert'sche Trägheitskraft) an:
sowie für die virtuelle Formänderungsenergie der beiden Ersatz-Federn:
.
Sortieren nach den virtuellen Verrückungen und anschrieben der Gleichgewichtsbedingungen in Matrix-Form liefert
.
Equilibrium Conditions
Text
1+1
tmp
Mit einer passenden Bezugszeit und -länge machen wir die Bewegungsgleichungen dimensionslos.
Hier liefert die Periodendauer der Plattform - allein, ohne Kugel - die Bezugszeit T. Die statische Absenkung der Plattform - ohne Einfluss der Kugel - liefert die Bezugslänge L.
Aus der Bewegungsgleichung oben lesen wir für K(u1-u2) = 0 ab:
und
.
Nun ist also
und
Die Kennlinie überführen wir entsprechend in
.
Einsetzen liefert die zwei Differentialgleichungen
.
Dimensionless Equations of Motion
Text
1+1
tmp
Für die numerische Lösung schreiben wir die zwei Bewegungsgleichung zweiter Ordnung um als vier Bewegungsgleichungen erster Ordnung zu
.
Die rechte Seite der gewöhnlichen Differentialgleichung ("Right-hand-side of ODE") lautet damit
Die dimensionslosen Parameter wählen wir zu
und lösen die Bewegungsgleichungen numerisch - hier mit dem Runge-Kutta-Verfahren 4.ter Ordnung.
Solving
Text
1+1
tmp
Als Lösung tragen wir die Zeitverläufe der Höhen U1, U2 über der Zeit τ
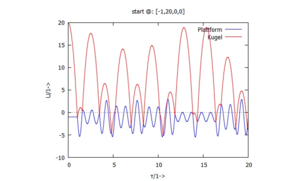
und U1, U2 jeweils über V1, V2 im Phasendiagramm auf:
Post-Processing
Text
1+1
| Kugel-Modell:
elast. Kontakt mit Einfederung w. | |
| 
|
Links
- ...
Literature
- ...