Gelöste Aufgaben/Kw23: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 11: | Zeile 11: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
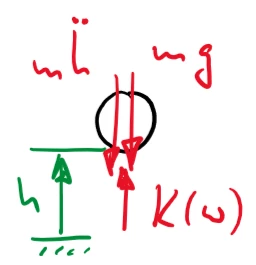
Eine Kugel (Masse m, Radius r) wird aus der Höhe H im Erdschwerefeld losgelassen, kommt auf den Boden auf und „springt“ dann wie ein Flummi auf und ab. Der Stoß zwischen Kugel und Oberfläche sei ideal-elastisch. Gefragt ist eine numerische Lösung des Problems als Anfangswertproblem. | |||
<onlyinclude> | Dabei modellieren Sie die Kugel als elastisch, die Unterlage als starr. Die Kugel können Sie sich so wie unten skizziert im unteren Teil durch eine Feder ersetzt denken.<onlyinclude> | ||
[[Datei: | [[Datei:Kw23-01.png|alternativtext=|links|mini|119x119px|Lageplan]] | ||
Gesucht ist | Eine elastische Kugel wird im Erdschwerefeld losgelassen und „springt“ wie ein Flummi auf und ab. Gesucht ist die n''umerische Lösung als Anfangswertproblem.'' | ||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Die Schwierigkeit kommt aus der Modellierung der Kontaktkraft zwischen Boden und Kugel. Oft reicht es, ein [https://de.wikipedia.org/wiki/Ph%C3%A4nomenologie phänomenologisches Modell] zu implementieren - also die Kontaktkraft als reine "Federkraft" zu interpretieren. | |||
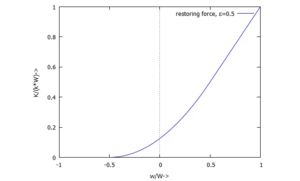
Die Federkraft K ist also Null, solange die Kugel die Oberfläche nicht berührt und sie sei hier - eine weitere drastische Vereinfachung - proportional zur Federkompression <nowiki>''</nowiki>w<nowiki>''</nowiki>, wenn sich Kugel und Oberfläche berühren | |||
==tmp== | ==tmp== | ||
| Zeile 32: | Zeile 34: | ||
<table class="wikitable" style="background-color:white; float: left"> | <table class="wikitable" style="background-color:white; float: left"> | ||
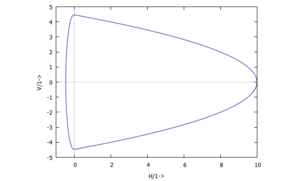
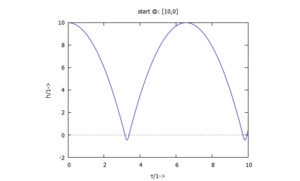
<tr><th></th><th></th></tr> | <tr><th>Kugel-Modell: elastischer Kontakt mit Einfederung <nowiki>''</nowiki>w<nowiki>''</nowiki> | ||
</th><th></th></tr> | |||
<tr><td>[[Datei:KW23-02.png|rahmenlos]]</td><td>[[Datei:Kw23-03.png|rahmenlos]]</td></tr> | <tr><td>[[Datei:KW23-02.png|rahmenlos]]</td><td>[[Datei:Kw23-03.png|rahmenlos]]</td></tr> | ||
</table> | </table> | ||
Version vom 27. März 2021, 07:19 Uhr
Aufgabenstellung
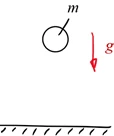
Eine Kugel (Masse m, Radius r) wird aus der Höhe H im Erdschwerefeld losgelassen, kommt auf den Boden auf und „springt“ dann wie ein Flummi auf und ab. Der Stoß zwischen Kugel und Oberfläche sei ideal-elastisch. Gefragt ist eine numerische Lösung des Problems als Anfangswertproblem.
Dabei modellieren Sie die Kugel als elastisch, die Unterlage als starr. Die Kugel können Sie sich so wie unten skizziert im unteren Teil durch eine Feder ersetzt denken.
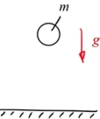
Eine elastische Kugel wird im Erdschwerefeld losgelassen und „springt“ wie ein Flummi auf und ab. Gesucht ist die numerische Lösung als Anfangswertproblem.
Lösung mit Maxima
Die Schwierigkeit kommt aus der Modellierung der Kontaktkraft zwischen Boden und Kugel. Oft reicht es, ein phänomenologisches Modell zu implementieren - also die Kontaktkraft als reine "Federkraft" zu interpretieren.
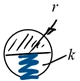
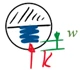
Die Federkraft K ist also Null, solange die Kugel die Oberfläche nicht berührt und sie sei hier - eine weitere drastische Vereinfachung - proportional zur Federkompression ''w'', wenn sich Kugel und Oberfläche berühren
tmp
Title
Text
1+1
| Kugel-Modell: elastischer Kontakt mit Einfederung ''w'' | |
|---|---|
 |  |
Links
- ...
Literature
- ...