Gelöste Aufgaben/Kv52: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 12: | Zeile 12: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:Kv52-01.png|alternativtext=|links|mini|233x233px|Lageplan]] | ||
Ein starrer Stab ''AB'' (Massenmoment ''J<sub>A</sub>'', Länge ''ℓ<sub>1</sub>'') wird aus dem Winkel ''φ<sub>0</sub>'' im Erdschwerefeld losgelassen und stößt in ''C'' auf einen Anschlag. Der Stoß zwischen Stab und Oberfläche sei ideal-elastisch. | |||
als Anfangswertproblem.</onlyinclude> | Gesucht ist die nichtlineare Bewegungsgleichung und die numerische Lösung als Anfangswertproblem.</onlyinclude> | ||
Dabei denken wir uns den Anschlag als elastische Feder, die nur für ''φ<-π/2'' Kontakt zum Stab hat. Die Federkraft ist also Null, solange der Stab die Oberfläche in ''C'' nicht berührt und sie ist proportional zur Federkompression ''w'', wenn sich Kugel und Oberfläche berühren. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
| Zeile 24: | Zeile 23: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir stellen die Bewegungsgleichungen des Systems als System con Differentialgleichungen erster Ordnung auf. Die Nichtlinearität kommt aus den großen Winkeln ''φ(t)'' und dem Kontakt mit der Wand. | ||
Mit unterschiedlichen Steifigkeiten für den Kontakt testen wir die Möglichkeiten der numerischen Integration aus.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
| Zeile 34: | Zeile 36: | ||
}} | }} | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die System-Parameter sind | ||
<math>\begin{array}{l}\ell_2 = \frac{3}{4}\ell_1\\J_A = \frac{1}{3}m\;\ell_1^2\end{array}</math>. | |||
Zum Dimensionslos-Machen der Bewegungsgleichungen brauchen wir später eine Bezugszeit ''t<sub>B</sub>'', die wir mit Hilfe der Eigenfrequenz der zugeordneten linearen Systems so wählen: | |||
<math>t_B = 1/\omega_0</math> | |||
(Achtung: das macht ''2π''-periodische Lösungen) | |||
Die Eigenkreisfrequenz bei Schwingungen um ''φ =-'' ''π/2'' herum ist | |||
<math>\displaystyle \omega_0^2 = \frac{m\,g\,\ell}{2\,J_A}</math> | |||
Außerdem wählen wir eine dimensionslose Federsteifigkeit ''κ'', so dass | |||
<math>\displaystyle k = \kappa\cdot \frac{m\,g}{\ell_2}</math>[[Datei:Kv52-02.png|mini|Kennlinie]]Für den nichtlinearen Kontakt wählen wir eine Kennlinie wie in [[Gelöste Aufgaben/Kw23|Kw23]] zu | |||
<math>C(\tilde{u},\varepsilon) = \left\{\begin{array}{ll}0&\text{ wenn } \tilde{u}<-\varepsilon\\\frac{1}{2}(\tilde{u}+\varepsilon)^2& \text{ wenn } -\varepsilon<\tilde{u}<\varepsilon \text{ und }\\\tilde{u}&\text{ sonst }\end{array}\right.</math> | |||
Und so wie rechts im Bild sieht sie dann aus:<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 43: | Zeile 66: | ||
}} | }} | ||
==tmp== | ==tmp== | ||
Die Gleichgewichtsbeziehungen erhalten wir aus einem Momentengleichgewicht um den Punkt A. | |||
<table class="wikitable"> | Das Freikörperbild <table class="wikitable"> | ||
<tr>< | <tr><td> | ||
[[Datei:Kv52-11.png|alternativtext=|rahmenlos|82x82px]] | |||
</td><td>[[Datei:Kv52-12.png|alternativtext=|rahmenlos|144x144px]] | |||
</td></tr> | |||
</table> | </table> | ||
<!--------------------------------------------------------------------------------> | liefert die Bewegungsgleichung | ||
<math>\displaystyle J_A\ddot{\varphi}-K(\varphi)\,\ell_2+m g \frac{\ell_1}{2} \cos(\varphi) = 0</math> | |||
Die Kontaktkraft konstruieren wir mit Hilfe der nichtlinearen Kennlinie ''C'' und | |||
<math>\displaystyle\tilde{u} = -\frac{\pi}{2} - \varphi</math> | |||
zu | |||
<math>K(\varphi) = \ell_2\cdot C(-\pi/2-\varphi,\varepsilon)</math>. | |||
Mit der dimensionslosen Zeit | |||
<math>\tau = t/t_B</math> | |||
finden wir als Bewegungsgleichung des Systems | |||
<math>\displaystyle \frac{d^2}{d\tau^2} \varphi + \cos(\varphi) - \frac{3}{2}\,\kappa \cdot C(-\pi/2-\varphi,\varepsilon)=0</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text=Text | |text=Text | ||
| Zeile 58: | Zeile 107: | ||
}} | }} | ||
==tmp== | ==tmp== | ||
Umschreiben in ein Differentialgleichungssystem erster Ordnung - wie wir es für die numerische Lösung brauchen - liefert | |||
<math>\left(\begin{array}{c}\dot{\varphi}\\\dot{\omega}\end{array}\right) = \left(\begin{array}{c}\omega\\\displaystyle \frac{3}{2}\,\kappa \cdot C(-\pi/2-\varphi,\varepsilon)-\cos(\varphi)\end{array}\right)</math>. | |||
Mit den Anfangsbedingungen | |||
<math>\begin{array}{l}\varphi(0) = 0\\\omega(0) = 0\end{array}</math> | |||
und einer Lösungsroutine nach dem [[Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Runge-Kutta-Verfahren 4.ter Ordnung|Runge-Kutta-Verfahren 4.ter Ordnung]] liefert das numerische Ergebnis. | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 67: | Zeile 127: | ||
}} | }} | ||
==tmp== | ==tmp== | ||
Wir tragen hier zwei Ergebnisse auf: | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
<table class="wikitable"> | <table class="wikitable"> | ||
<tr><th></th><th></th></tr> | <tr><th>... in dieser Spalte den Referenzfall | ||
<tr><td></td><td></td></tr> | |||
</table> | für <math>\kappa = 100.</math> | ||
</th><th>... und hier | |||
für <math>\kappa = 1000.</math> | |||
</th></tr> | |||
<tr><td>zunächst im Zeitbereich | |||
</td><td></td></tr><tr><td>[[Datei:Kv52-14.png|alternativtext=|rahmenlos]]</td><td></td></tr><tr><td>und dann im Phasenraum:</td><td></td></tr><tr><td>[[Datei:Kv52-15.png|alternativtext=|rahmenlos]]</td><td></td></tr></table> | |||
Im Referenzfall erhalten wir - wie erhofft - eine periodische Lösung: die Phasenkurve ist geschlossen. Schon für eine um den Faktur 10 größere Steifigkeit des Anschlags jedoch weicht die Lösung sichtbar von einer periodischen ab. Das klassische Problem von numerischen Integrationsroutinen wird hier sichtbar. | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
| Zeile 84: | Zeile 155: | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<hr/> | <hr/> | ||
Version vom 26. März 2021, 10:59 Uhr
Aufgabenstellung
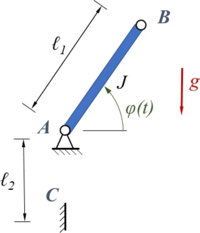
Ein starrer Stab AB (Massenmoment JA, Länge ℓ1) wird aus dem Winkel φ0 im Erdschwerefeld losgelassen und stößt in C auf einen Anschlag. Der Stoß zwischen Stab und Oberfläche sei ideal-elastisch.
Gesucht ist die nichtlineare Bewegungsgleichung und die numerische Lösung als Anfangswertproblem. Dabei denken wir uns den Anschlag als elastische Feder, die nur für φ<-π/2 Kontakt zum Stab hat. Die Federkraft ist also Null, solange der Stab die Oberfläche in C nicht berührt und sie ist proportional zur Federkompression w, wenn sich Kugel und Oberfläche berühren.
Lösung mit Maxima
Lorem Ipsum ....
tmp
Wir stellen die Bewegungsgleichungen des Systems als System con Differentialgleichungen erster Ordnung auf. Die Nichtlinearität kommt aus den großen Winkeln φ(t) und dem Kontakt mit der Wand.
Mit unterschiedlichen Steifigkeiten für den Kontakt testen wir die Möglichkeiten der numerischen Integration aus.
Header
Text
1+1
tmp
Die System-Parameter sind
.
Zum Dimensionslos-Machen der Bewegungsgleichungen brauchen wir später eine Bezugszeit tB, die wir mit Hilfe der Eigenfrequenz der zugeordneten linearen Systems so wählen:
(Achtung: das macht 2π-periodische Lösungen)
Die Eigenkreisfrequenz bei Schwingungen um φ =- π/2 herum ist
Außerdem wählen wir eine dimensionslose Federsteifigkeit κ, so dass
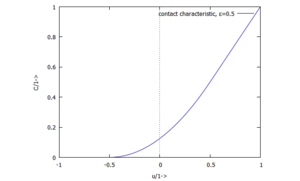
Für den nichtlinearen Kontakt wählen wir eine Kennlinie wie in Kw23 zu
Und so wie rechts im Bild sieht sie dann aus:
Declarations
Text
1+1
tmp
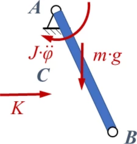
Die Gleichgewichtsbeziehungen erhalten wir aus einem Momentengleichgewicht um den Punkt A.
Das Freikörperbild
|
| 
|
liefert die Bewegungsgleichung
Die Kontaktkraft konstruieren wir mit Hilfe der nichtlinearen Kennlinie C und
zu
.
Mit der dimensionslosen Zeit
finden wir als Bewegungsgleichung des Systems
.
Equilibrium Conditions
Text
1+1
tmp
Umschreiben in ein Differentialgleichungssystem erster Ordnung - wie wir es für die numerische Lösung brauchen - liefert
.
Mit den Anfangsbedingungen
und einer Lösungsroutine nach dem Runge-Kutta-Verfahren 4.ter Ordnung liefert das numerische Ergebnis.
Solving
Text
1+1
tmp
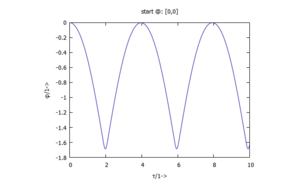
Wir tragen hier zwei Ergebnisse auf:
| ... in dieser Spalte den Referenzfall
für | ... und hier
für |
|---|---|
| zunächst im Zeitbereich | |
 | |
| und dann im Phasenraum: | |
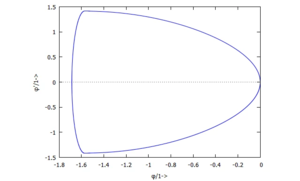 |
Im Referenzfall erhalten wir - wie erhofft - eine periodische Lösung: die Phasenkurve ist geschlossen. Schon für eine um den Faktur 10 größere Steifigkeit des Anschlags jedoch weicht die Lösung sichtbar von einer periodischen ab. Das klassische Problem von numerischen Integrationsroutinen wird hier sichtbar.
Post-Processing
Text
1+1
Links
- ...
Literature
- ...