Gelöste Aufgaben/Kit5: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 15: | Zeile 15: | ||
In ''B'' hält das verschiebliche Lager den Balken horizontal. Gegen über Punkt A hält das Lager in B den Balken in einem vertikalen Abstand von W zur Horizontalen. | In ''B'' hält das verschiebliche Lager den Balken horizontal. Gegen über Punkt A hält das Lager in B den Balken in einem vertikalen Abstand von W zur Horizontalen. | ||
<onlyinclude>[[Datei:Datei:Kit5.png.png|250px|left|mini|Lageplan]] | <onlyinclude>[[Datei:Datei:Kit5.png.png|250px|left|mini|Lageplan|verweis=Special:FilePath/Datei:Kit5.png.png]] | ||
Gesucht ist die Biegelinie des Balkens, der durch geometrische Randbedingungen vorverformt ist. | Gesucht ist die Biegelinie des Balkens, der durch geometrische Randbedingungen vorverformt ist. | ||
</onlyinclude> | </onlyinclude> | ||
| Zeile 33: | Zeile 33: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Damit es einfacher wird, lassen Tilde über ''w'' weg. Die Bewegungsgleichung für beide Bereiche ist dann | ||
<math>w''''(\xi)=\mu</math> | |||
und deren allgemeine Lösung | |||
<math>\begin{array}{l} \displaystyle {{w}_{1}}\left( \xi\right) :=\frac{\mu\cdot {{\xi}^{4}}}{24}+\frac{{{C}_{1,3}}\cdot {{\xi}^{3}}}{6}+\frac{{{C}_{1,2}}\cdot {{\xi}^{2}}}{2}+{{C}_{1,1}}\cdot \xi+{{C}_{1,0}} \\ \displaystyle {{w}_{2}}\left( \xi\right) :=\frac{{{C}_{2,3}}\cdot {{\xi}^{3}}}{6}+\frac{{{C}_{2,2}}\cdot {{\xi}^{2}}}{2}+{{C}_{2,1}}\cdot \xi+{{C}_{2,0}} \text{ (hier ist } \mu=0 )\end{array}</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Lösen der dimensionslosen Bewegungsgleichung | {{MyCodeBlock|title=Lösen der dimensionslosen Bewegungsgleichung | ||
|text=Text | |text=Text | ||
| Zeile 44: | Zeile 51: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Einsetzten der Lösung der Bewegungsgleichungen in die Randbedingungen liefert die Gleichungen | ||
<math>\begin{pmatrix}{{C}_{1,0}}=0\\ {{C}_{1,1}}=\displaystyle \frac{1}{10}\\ \displaystyle \frac{\mu}{24}+\frac{{{C}_{1,3}}}{6}+\frac{{{C}_{1,2}}}{2}+{{C}_{1,1}}+{{C}_{1,0}}={{C}_{2,0}}\\ \displaystyle \frac{\mu}{6}+\frac{{{C}_{1,3}}}{2}+{{C}_{1,2}}+{{C}_{1,1}}={{C}_{2,1}}\\ | |||
\displaystyle \frac{\mu}{2}+{{C}_{1,3}}+{{C}_{1,2}}={{C}_{2,2}}\\ \mu+{{C}_{1,3}}={{C}_{2,3}}\\ \displaystyle \frac{{{C}_{2,3}}}{8}+\frac{{{C}_{2,2}}}{2}+{{C}_{2,1}}=0\\ \displaystyle \frac{{{C}_{2,3}}}{48}+\frac{{{C}_{2,2}}}{8}+\frac{{{C}_{2,1}}}{2}+{{C}_{2,0}}=1\end{pmatrix}</math> | |||
mit den Unbekannten | |||
<math>\underline{x} = \begin{pmatrix}{{C}_{1,0}}\\ {{C}_{1,1}}\\ {{C}_{1,2}}\\ {{C}_{1,3}}\\ {{C}_{2,0}}\\ {{C}_{2,1}}\\ {{C}_{2,2}}\\{{C}_{2,3}}\end{pmatrix}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formulation of Boundary Conditions | {{MyCodeBlock|title=Formulation of Boundary Conditions | ||
|text=Text | |text=Text | ||
| Zeile 54: | Zeile 69: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Das Gleichungssystem | ||
<math>\underline{\underline{A}}\cdot\underline{x} = \underline{b}</math> | |||
hat dabei die Koeffizientenmatrix | |||
<math>\underline{\underline{A}} = \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & 1 & \frac{1}{2} & \frac{1}{6} & -1 & 0 & 0 & 0\\ 0 & 1 & 1 & \frac{1}{2} & 0 & -1 & 0 & 0\\ 0 & 0 & 1 & 1 & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & -1\\ 0 & 0 & 0 & 0 & 0 & 1 & \frac{1}{2} & \frac{1}{8}\\ 0 & 0 & 0 & 0 & 1 & \frac{1}{2} & \frac{1}{8} & \frac{1}{48}\end{pmatrix} | |||
</math> | |||
sowie die rechte Seite | |||
<math>\underline{b} = \begin{pmatrix}0\\ \frac{1}{10}\\ -\frac{\mu}{24}\\ -\frac{\mu}{6}\\ -\frac{\mu}{2}\\ -\mu\\ 0\\ 1\end{pmatrix}</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=The Equations of Motion | {{MyCodeBlock|title=The Equations of Motion | ||
|text=Text | |text=Text | ||
| Zeile 64: | Zeile 91: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Wir erhalten | ||
{{MyCodeBlock|title=Solving | |||
<math>[{{C}_{1,0}}=0,{{C}_{1,1}}=\frac{1}{10},{{C}_{1,2}}=\frac{72+5\cdot \mu}{30},{{C}_{1,3}}=-\frac{444+95\cdot \mu}{135},{{C}_{2,0}}=\frac{2436+25\cdot \mu}{3240},{{C}_{2,1}}=-\frac{5\cdot \mu-231}{270},{{C}_{2,2}}=-\frac{24+\mu}{27},{{C}_{2,3}}=\frac{40\cdot \mu-444}{135}]</math>.<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 74: | Zeile 102: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | [[Datei:Kit5-12.png|mini|w(x)]] | ||
Die Lösung plotten wir, z.B. für die Streckenlast ''μ=100'': | |||
Die dimensionslose Auslenkung ist jetzt etwas größer als "1" - Sie müssen sich also jetzt überlegen, ob Ihre Theorie noch gültig ist!<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text=Text | |text=Text | ||
| Zeile 92: | Zeile 124: | ||
Version vom 26. März 2021, 07:05 Uhr
Aufgabenstellung
Bei diesem Randwertproblem wird ein Euler-Bernoulli-Balken (Elastizitätsmodul E, Flächenmoment 2-ten Grades I) mit einer Streckenlast q0 im Bereich A-B belastet. In A ist der Balken fest eingespannt, wobei durch eine Einbau-Ungenauigkeit der Rand im Verhältnis 1:10 geneigt ist.
In B hält das verschiebliche Lager den Balken horizontal. Gegen über Punkt A hält das Lager in B den Balken in einem vertikalen Abstand von W zur Horizontalen.
Gesucht ist die Biegelinie des Balkens, der durch geometrische Randbedingungen vorverformt ist.
Lösung mit Maxima
In Kit4 finden Sie die Transformation der Bewegungsgleichung des Euler-Bernoulli-Balkens in die dimensionslose Form mit der allgemeinen Lösung
für die Bereiche i=1 (A-B) und i=2 (B-C).
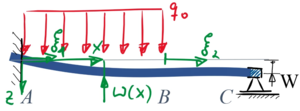
Dazu gehören die neuen dimensionslose Koordinaten ξ1 und ξ2:
Die Rand- und Übergangsbedingungen lauten dann mit ℓ2 = ℓ1/2
, ,
tmp
Damit es einfacher wird, lassen Tilde über w weg. Die Bewegungsgleichung für beide Bereiche ist dann
und deren allgemeine Lösung
Lösen der dimensionslosen Bewegungsgleichung
Text
1+1
tmp
Einsetzten der Lösung der Bewegungsgleichungen in die Randbedingungen liefert die Gleichungen
mit den Unbekannten
.
Formulation of Boundary Conditions
Text
1+1
tmp
Das Gleichungssystem
hat dabei die Koeffizientenmatrix
sowie die rechte Seite
The Equations of Motion
Text
1+1
tmp
Wir erhalten
.===Solving=== Text
1+1
tmp
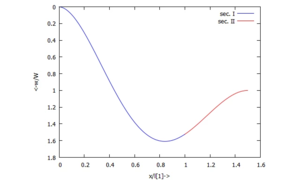
Die Lösung plotten wir, z.B. für die Streckenlast μ=100:
Die dimensionslose Auslenkung ist jetzt etwas größer als "1" - Sie müssen sich also jetzt überlegen, ob Ihre Theorie noch gültig ist!
Post-Processing
Text
1+1
Links
- ...
Literature
- ...