Gelöste Aufgaben/Kit5

Aufgabenstellung

Bei diesem Randwertproblem wird ein Euler-Bernoulli-Balken (Elastizitätsmodul E, Flächenmoment 2-ten Grades I) mit einer Streckenlast q₀ im Bereich A-B belastet. In A  ist der Balken fest eingespannt, wobei durch eine Einbau-Ungenauigkeit der Rand im Verhältnis 1:10 geneigt ist.

In B hält das verschiebliche Lager den Balken horizontal. Gegen über Punkt A hält das Lager in B den Balken in einem vertikalen Abstand von W zur Horizontalen.

Datei:Datei:Kit5.png.png

Lageplan

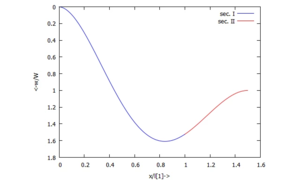
Gesucht ist die Biegelinie des Balkens, der durch geometrische Randbedingungen vorverformt ist.

Lösung mit Maxima

In Kit4 finden Sie die Transformation der Bewegungsgleichung des Euler-Bernoulli-Balkens in die dimensionslose Form mit der allgemeinen Lösung

$\displaystyle {{\tilde {w}}_{i}}\left(\xi \right):={\frac {\mu \cdot {{\xi }^{4}}}{24}}+{\frac {{{C}_{i,3}}\cdot {{\xi }^{3}}}{6}}+{\frac {{{C}_{i,2}}\cdot {{\xi }^{2}}}{2}}+{{C}_{i,1}}\cdot \xi +{{C}_{i,0}}$

für die Bereiche i=1 (A-B) und i=2 (B-C).

Koordinaten

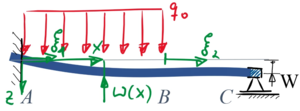
Dazu gehören die neuen dimensionslose Koordinaten ξ₁ und ξ₂:

Die Rand- und Übergangsbedingungen lauten dann mit ℓ₂ = ℓ₁/2

${\begin{array}{ccl}{\tilde {w}}_{1}(0)&=&0\\{\tilde {w}}'_{1}(0)&=&1/10\end{array}}$, ${\begin{array}{ccl}{\tilde {w}}_{1}(1)&=&{\tilde {w}}_{2}(0)\\{\tilde {w}}'_{1}(1)&=&{\tilde {w}}'_{2}(0)\\{\tilde {w}}''_{1}(1)&=&{\tilde {w}}''_{2}(0)\\{\tilde {w}}'''_{1}(1)&=&{\tilde {w}}'''_{2}(0)\end{array}}$, ${\begin{array}{ccl}{\tilde {w}}_{1}(1/2)&=&W\\{\tilde {w}}'_{2}(1/2)&=&0\end{array}}$

tmp

Lösen der dimensionslosen Bewegungsgleichung

Text

1+1

tmp

Formulation of Boundary Conditions

Text

1+1

tmp

The Equations of Motion

Text

1+1

tmp

Solving

Text

1+1

tmp

Post-Processing

Text

1+1

w(x)

---

Links

• ...

Literature

• ...