Gelöste Aufgaben/Kerb

Aufgabenstellung

Ein Satellit soll eine stabile Umlaufbahn um die Erde beschrieben.

Berechnen Sie mögliche Lösungen.

Lösung mit Maxima

Bei unserer Suche geht es um kartesische- und polare-Koordinatensysteme, Gleichgewichtsbedingungen formuliert mit dem Prinzip der virtuellen Verrückungen und er Stabilität von Lösungen.

tmp

Header

Ein Satellit im Orbit ist einer Erdbeschleunigung g ausgesetzt, die nichtlinear von seinem Abstand zum Erdmittelpunkt abhängt. Dieses nichtlineare Anfangswertproblem lösen wir hier als Anfangswertproblem numerisch.

/*********************************************************/
/* MAXIMA script                                         */
/* version: wxMaxima 15.08.2                             */
/* author: Andreas Baumgart                              */
/* last updated: 2018-03-21                              */
/* ref: Kerb (TM-C, Labor 6)                             */
/* description: finds persiod solution for               */
/*              the tracectory of a satellite            */
/*********************************************************/

tmp

Declarations

Wir brauchen die Systemparameter 

Symbol	Bedeutung
R = 6378,137 km	Erdradius am Äquator
g0 = 9.81 m/s2	Erdbeschleunigung an der Erdoberfläche
T = 1 d	Periodendauer einer Erdumdrehung (d .. day)
Or = 35786 km	Höhe eines Satelliten über der Erdoberfläche in einem geostationären Orbit.

/*********************************************************/
/* declarations */
/* declare variational variables - see 6.3 Identifiers   */
declare("δW", alphabetic);
declare("δr", alphabetic);
declare("δu", alphabetic);
declare("δφ", alphabetic);

assume(R>0, g>0, rho>0, mu>0, T>0);

/* parameter */
params: [R = 6378137*m,    /* earth radius at equator */
         g = 9.81*m/s^2,   /* gravitational constant  */
         T = 24*60*60*s];  /* 24 hours                */
verify: [O=R+35786000*m];  /* geostat. orbit          */
dimles: [g=mu*R/T^2];      /* dimensionless parameter */

Kinematics

Wir führen ein kartesisches x, y, z - Koordinaten-System im Erdmittelpunkt (earth-centered inertial) ein, das nicht mit der Erde mitrotiert - wir setzen dieses als Intertialsystem an (obwohl wir wissen, dass die Erde um die Sonne rotiert und die Sonne selbst auch kein Intertialsystem in unserem Sinne ist).

Satellite in Orbit

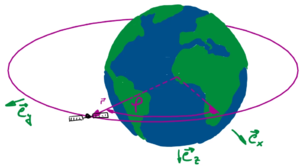
Wir brauchen die Einheitsvektoren

${\vec {e}}_{x},{\vec {e}}_{y}$

entlang der x,y-Achsen, um den Ortsvektor zum Satelliten

${\vec {r}}=r(t)\cdot {\vec {e}}_{r}(t)$

zu erfassen.

Dafür verwenden wir

${\vec {e}}_{r}(t)=\cos(\varphi (t))\cdot {\vec {e}}_{x}+\sin(\varphi (t))\cdot {\vec {e}}_{y}$.

Die Bewegung des Satelliten können wir also auch in kartesischen Koordinarten

${\begin{array}{l}u_{x}(t)=r(t)\cdot \cos(\varphi (t))\\u_{y}(t)=r(t)\cdot \sin(\varphi (t))\end{array}}$,

anschreiben, was hier allerdings wenig anschaulich ist! Für die Variation von u_x, u_y erhalten wir

${\begin{array}{l}\delta u_{x}=\cos(\varphi (t))\cdot \delta r-r(t)\cdot \sin(\varphi (t))\cdot \delta \varphi \\\delta u_{y}=\sin(\varphi (t))\cdot \delta r+r(t)\cdot \cos(\varphi (t))\cdot \delta \varphi \end{array}}$

XX

tmp

Equilibrium Conditions

..

XX

tmp

Stationary Solution

..

XX

tmp

Solving

..

XX

tmp

Post-Processing

..

XX

---

Links

• ...

Literature

• ...

Video laden

Lokale Datei

Lokale Datei sammelt möglicherweise persönliche Daten.

FortfahrenAusblenden

Trajectory animation

Phasen-Diagramme

Phasengeschwindigkeit

Weg-Zeit-Diagramm