Gelöste Aufgaben/Kerb: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
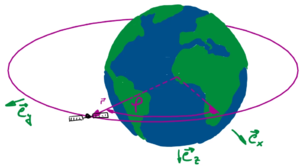
Satellite in Orbit Trajectory animation 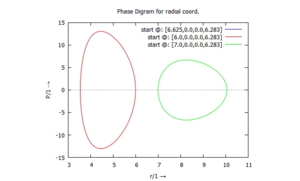
Phasen-Diagramme 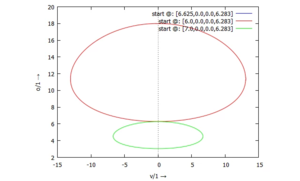
Phasengeschwindigkeit 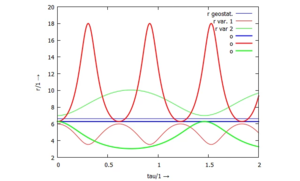
Weg-Zeit-Diagramm
| Zeile 43: | Zeile 43: | ||
<table class="wikitable"> | <table class="wikitable"> | ||
<tr><th></th><th></th></tr> | <tr><th>Symbol</th><th>Bedeutung</th></tr> | ||
<tr><td></td><td></td></tr> | <tr><td>R = 6378,137 km</td><td>Erdradius am Äquator</td></tr> | ||
<tr><td>g<sub>0</sub> = 9.81 m/s2</td><td>Erdbeschleunigung an der Erdoberfläche</td></tr> | |||
<tr><td>T = 1 d</td><td>Periodendauer einer Erdumdrehung (d .. day)</td></tr> | |||
<tr><td>O<sub>r</sub> = 35786 km</td><td>Höhe eines Satelliten über der Erdoberfläche in einem geostationären Orbit.</td></tr> | |||
</table> | </table> | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
Version vom 25. März 2021, 08:51 Uhr
Aufgabenstellung

Ein Satellit soll eine stabile Umlaufbahn um die Erde beschrieben.
Berechnen Sie mögliche Lösungen.
Lösung mit Maxima
Bei unserer Suche geht es um kartesische- und polare-Koordinatensysteme, Gleichgewichtsbedingungen formuliert mit dem Prinzip der virtuellen Verrückungen und er Stabilität von Lösungen.
tmp
Header
Ein Satellit im Orbit ist einer Erdbeschleunigung g ausgesetzt, die nichtlinear von seinem Abstand zum Erdmittelpunkt abhängt. Dieses nichtlineare Anfangswertproblem lösen wir hier als Anfangswertproblem numerisch.
/*********************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2018-03-21 */
/* ref: Kerb (TM-C, Labor 6) */
/* description: finds persiod solution for */
/* the tracectory of a satellite */
/*********************************************************/
tmp
Declarations
Wir brauchen die Systemparameter
| Symbol | Bedeutung |
|---|---|
| R = 6378,137 km | Erdradius am Äquator |
| g0 = 9.81 m/s2 | Erdbeschleunigung an der Erdoberfläche |
| T = 1 d | Periodendauer einer Erdumdrehung (d .. day) |
| Or = 35786 km | Höhe eines Satelliten über der Erdoberfläche in einem geostationären Orbit. |
/*********************************************************/
/* declarations */
/* declare variational variables - see 6.3 Identifiers */
declare("δW", alphabetic);
declare("δr", alphabetic);
declare("δu", alphabetic);
declare("δφ", alphabetic);
assume(R>0, g>0, rho>0, mu>0, T>0);
/* parameter */
params: [R = 6378137*m, /* earth radius at equator */
g = 9.81*m/s^2, /* gravitational constant */
T = 24*60*60*s]; /* 24 hours */
verify: [O=R+35786000*m]; /* geostat. orbit */
dimles: [g=mu*R/T^2]; /* dimensionless parameter */
tmp
Kinematics
..
XX
tmp
Equilibrium Conditions
..
XX
tmp
Stationary Solution
..
XX
tmp
Solving
..
XX
tmp
Post-Processing
..
XX
Links
- ...
Literature
- ...



