Gelöste Aufgaben/JUMP/Driver Controls: Unterschied zwischen den Versionen
| Zeile 36: | Zeile 36: | ||
::<math>\begin{array}{ll} | ::<math>\begin{array}{ll} | ||
e_1 &= | e_1 &= f_1(\tilde{v}) \text{ with } \tilde{v} = \frac{\displaystyle v_{rel}}{\displaystyle v_{\varepsilon}}; \text{ here we choose }\\ | ||
&= 1 | &= 1+\tilde{v} | ||
\end{array}</math> | \end{array}</math> | ||
| Zeile 43: | Zeile 43: | ||
::<math>\begin{array}{ll} | ::<math>\begin{array}{ll} | ||
e_2 &= | e_2 &= f_2(\tilde{v}) \text{ with } \tilde{v} = \frac{\displaystyle v_{c}}{\displaystyle V_{set}}; \text{ here we choose }\\ | ||
&= 1-\tilde{v} | &= 1-\tilde{v} | ||
\end{array}</math>. | \end{array}</math>. | ||
The | The functions for ''e<sub>1</sub>'' ensures that "''p"'' increases e.g. if ''v<sub>rel</sub>'' < ''v<sub>ε</sub>'' and decreases otherwise. [[Datei:JUMP-driver-blockdiagram-controller.png|mini|Block-diagram controller]]With controller parameters ''K<sub>p</sub>, Ki, K<sub>d</sub>'' we get this diagram for the controlled system. | ||
When e_1 / e_2 | |||
The controller adds thus adds the state variable | The controller adds thus adds the state variable | ||
Version vom 22. März 2021, 15:29 Uhr

Since we’re in a 2D-simulation environment, the driver controls only “gas” (acceleration) and breaks - no directional control needed to be taken into account.
Scope

The track poses challenges that require the driver to control the driving and breaking torque on the wheel. These track-specific challenges include
- achieving maximum acceleration, thus avoiding wheel-skid and adjusting to a slip that provides optimal traction,
- achieving maximum deceleration when breaking and therefore avoiding wheels becoming locked,
- avoiding excessive battery-temperatures and thus controlling driving torque.
Structure
The driver is tasked to control wheel slip and wheel skid via the "gas"-pedal. We differentiate between
- slip as the relative micro-velocity necessary to transmit forces in rolling contact and
- skip as unwanted excessive relative velocity resulting from poor torque-control at the wheels.
The information for this task come as "info" from the car's motion.
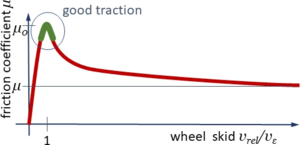
To avoid wheel skid and to control slip, the driver will aim to maintain a relative velocity at the wheel-contact point “C“ around the small velocity vε, thus reducing torque MW if vrel > vε and increasing MW if vrel < vε.
This is a very challenging system to be controlled because
- the velocity domain that we target is rather small and
- the characteristic for vrel > vε is degressive: the friction force decreases with relative velocity.
Model
The most common controller in technical applications is a PID-controller. Our target value to control is both
- the slip-velocity vrel with set-point and
- the cruising-velocoty vc with set-point .
We define the error values e for both as
and
- .
The functions for e1 ensures that "p" increases e.g. if vrel < vε and decreases otherwise.
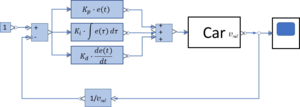
With controller parameters Kp, Ki, Kd we get this diagram for the controlled system.
When e_1 / e_2
The controller adds thus adds the state variable
to the system. And we need to find
as the rate of change from the Car-Body-Model.
So the only state variable from the driver is
- .
The output "p" of the submodel is not a state variable, but
Variables
| name | symbol | unit |
|---|---|---|
| integrator part of PID controller | E(t) | 1 |
Parameter
| name | symbol | value | unit |
|---|---|---|---|
| coefficient of proportional contribution | Kp | 1/s | |
| coefficient of integrator contribution | Ki | 100 | 1/s^2 |
| coefficient of differential contribution - not employed | Kd | 1 | |
| max. tolerated battery temperature | TB,max | 60 | °C |
| target-speed (choose very high when you want "pedal to the metal") | Vset | 10 | m/s |
next workpackage: e-motor and drive-train →
References
- Yuan, Lei; Chen, Hong; Ren, Bingtao; Zhao, Haiyan: Model predictive slip control for electric vehicle with four in-wheel motors, Proceedings of the 34th Chinese Control Conference July 28-30, 2015, Hangzhou, China, p 7895-7900
- ...