Gelöste Aufgaben/JUMP/Battery

← Back to Start

Scope

Our Block-Diagram

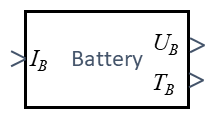
The battery is our power-supply. Depending on the discharging current I_B consumed by our drive-train, the battery will display a voltage U_B.

We are looking for a mathematical model that accounts for discharging operations only and we are not interested in high-frequency load-idle-cycles. Long-term changes of battery-parameters are out of scope.

We copy the typical specifications for a LiPo battery used for RC Model Cars to be:

• total capacity: Q_B0 = 5000 mAh,
• voltage: U_B0 = 11.1 V,
• C-rating: 25.

The C-rating refers to the rate of energy the battery can safely discharge continuously, represented in terms of current as a multiple of its overall capacity. The maximum continuous current for this battery is

${\begin{array}{ll}I_{B,max}&=5000\;mAh\cdot 25\cdot 1/h\\&=125A\end{array}}$

Also we need to model the battery heat to avoid excessive temperatures T_B of the battery.

Structure

Our model accounts for two aspects:

1. power delivery and
2. temperature.

Both aspects are related in the sense that discharging operations with high currents lead to high battery-temperatures which will reduce the effective battery capacity.

The equivalent block-diagram of our model is this:

The battery-current I_B entails a battery voltage U_B and Temperature T_B.

Power Delivery

Battery Equivalent Circuit Diagram

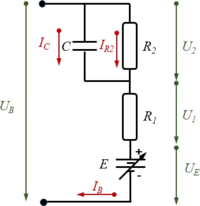
We employ a standard battery model which accounts for

• E: the equilibrium potential
• R₁, R₂: two internal resistances and
• C: an effective capacitance.

In a steady-state-condition, the battery voltage U_B is thus a function of the battery current I_B.

Temperature

Battery Heat Rates.

Our simple lumped-body model accounts for heat generation inside the battery and heat dissipation over its surface.

In steady-state condition, they are equal, if heat generation ${\dot {Q}}_{H}$ exceeds heat dissipation ${\dot {Q}}_{D}$, the battery heat increases - und thus its temperature.

Model

Power Delivery

Using Kirchhoff’s laws and from the model-diagram of the electric-circuit of the battery, we find the equilibrium conditions

${\begin{array}{ll}U_{B}&=U_{1}+U_{2}+E(S_{D}){\text{ where }}E(S_{D}):=U_{E}{\text{ and }}\\I_{B}&=I_{C}+I_{R2}\end{array}}$.

The potential E is a function of the effective battery capacity or the commonly used dimensionless “state of dischange”

$S_{D}={\frac {\displaystyle Q_{B0}-Q_{B}(t)}{\displaystyle Q_{B0}}}$.

Characteristic of Electrochemical Potential.

E(S_D) depends in a complex way on the electrochemical processes within the battery. We account for this functional relationship using a characteristic curve which we copy from literature.

In operation, the reference battery capacity Q_B0 is being consumed by the current I_B, thus

${\dot {Q}}_{B}=-\alpha (I_{B})\cdot \beta (T_{B})\cdot I_{B}$,

where α is a correction-factor accounting for the current I_B and β accounting for the battery-temperature T_B. The effect of α can be seen in the diagram above where I_e > I_ref.

For a representation of this function, we choose an appropriate polynomial with

${\begin{array}{lcl}e(S_{D})&:=&{\frac {\displaystyle E(Q_{B})}{\displaystyle U_{0}}}\\&=&\displaystyle \sum _{0}^{5}C_{i}\cdot S_{D}^{i}\end{array}}$

Its unknown coefficients C_i will be identified from the characteristic above. The components of the electric circuit provide these equations

${\begin{array}{ll}U_{1}&=R_{1}\cdot I_{B},\\U_{2}&=R_{2}\cdot I_{R2},\\I_{C}&=C\cdot {\frac {\displaystyle dU_{2}}{\displaystyle dt}}.\end{array}}$

with α, β being current- and temperature-related correction factors respectively.

With the nominal battery capacity Q_B0 and the actual capacity Q_B, we have the commonly employed state of discharge S_D to be

${\begin{array}{ll}S_{D}&={\frac {\displaystyle 1}{\displaystyle Q_{B0}}}\cdot \displaystyle \int _{0}^{t}\alpha (I_{B})\cdot \beta (T)\cdot I_{B}dt\\&=1-{\frac {\displaystyle Q_{B}(t)}{\displaystyle Q_{B0}}}.\end{array}}$

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 18.10.1                           */
/* author: Andreas Baumgart                            */
/* last updated: 2021-02-08                            */
/* ref: Modelling and Simulation (TUAS)                */
/* description: Rounding between straight line-segments*/
/*******************************************************/

/*******************************************************/
/* declarations                                        */
/*******************************************************/
declare("ω",alphabetic);
declare("α",alphabetic);
declare("β",alphabetic);

/*******************************************************/
/* equations of motion                                 */
/*******************************************************/
/* Kirchhoff's law     */
KL : [U[0] = E+U[1]+U[2],
      U[1] = R[1]*I[1],
      U[2] = R[2]*I[2],
      I[1] = I[2]+I[C],
      I[C] = C*'diff(U[2],t),
      'diff(Q[B],t) = α*β*I[1],
      s = Q[B]/Q[R],
      /*             */
      m[B]*c[PB]*'diff(T[B],t)=R[1]*I[1]^2+R[2]*I[2]^2-H[B]*(T[B]-T[0])];

battery: ratsimp([subst(KL[2],KL[1]),
                  subst(solve(KL[3],I[2]), subst(solve(KL[4],I[C]), solve(KL[5],'diff(U[2],t))[1])),
		  KL[6],KL[7],KL[8]]);

/* Characteristic curve for E */
/*                            */
E(s) := sum(c[i]*s^i,i,0,5);

bc : [subst([s=0],E(s))=V[0],E(1)=0,
      subst([s=0],diff(E(s),s))=S[0],subst([s=1],diff(E(s),s))=S[2],
      E(6/10)=V[1],subst([s=6/10],diff(E(s),s))=S[1]];

params: [V[0]=4,S[0]=-1.5,V[1]=3.7,S[1]=-0.4,S[2]=-30];

sol : solve(subst(params,bc),makelist(c[i],i,0,5))[1];
plot2d(subst(sol,E(s)),[s,0,1], [xlabel,"SoD"], [ylabel,"U[0]"]);

Temperature

The thermodynamic balance-equation of heat yields

${\dot {Q}}_{T}={\dot {Q}}_{H}-{\dot {Q}}_{D}$.

✔ Nomenclature "Q":

Note that Q is used here as the heat of the battery – not as the battery-capacity as above!

The battery heat is a function of

• temperature T_B,
• averaged specific heat capacity c_p,B and
• battery mass m_B.

so that

${\dot {Q}}_{T}=m_{B}\cdot c_{B}\cdot {\frac {\displaystyle dT}{\displaystyle dt}}$.

Heat generation inside the battery be

${\dot {Q}}_{H}=R_{1}\cdot I_{B}^{2}+R_{2}\cdot I_{R2}^{2}$.

and heat dissipation

${\dot {Q}}_{D}=h_{B}\cdot (T_{B}-T_{0})$

with ambient air temperature T₀ and the coefficient of heat transfer h_B.

/* none given */

Summary

Thus, the battery-coordinates are

${\underline {q}}_{B}=\left({\begin{array}{c}Q_{B}(t)\\U_{2}(t)\\T_{B}(t)\end{array}}\right)$

with the associated equations of motion

${\begin{array}{ll}{\dot {Q}}_{B}&=-\alpha (I_{B})\cdot \beta (T)\cdot I_{B}{\text{ and }}S_{D}&={\frac {\displaystyle Q_{B}(t)-Q_{B0}}{\displaystyle Q_{B0}}},\\{\dot {U}}_{2}&={\frac {\displaystyle I_{C}}{\displaystyle C}},\\{\dot {T}}_{B}&={\frac {\displaystyle 1}{\displaystyle m_{B}\;c_{B}}}\cdot \left({\dot {Q}}_{H}-{\dot {Q}}_{D}\right)\\\end{array}}$

and additional algebraic equation

${\begin{array}{ll}{\dot {Q}}_{H}&=R_{1}\cdot I_{B}^{2}+R_{2}\cdot I_{2}^{2}{\text{ where }}I_{2}={\frac {\displaystyle U_{2}}{\displaystyle R_{2}}}\\U_{B}&=R_{1}\cdot I_{B}+U_{2}+E(S_{D}),\\{\dot {Q}}_{D}&=H_{B}\cdot (T_{B}(t)-T_{0}).\end{array}}$

Variables

name	symbol	unit
battery remaining capacity	QB	A h
capacitance voltage	UB2	V
battery temperature	TB	°C

Parameters

The coefficients C_i for e(S_D) have been computed from conditions for a 5th-order polynomial by defining function-values and gradients at reference points:

$C_{0}={\frac {11}{10}},C_{1}=-1,C_{2}={\frac {1177}{240}},C_{3}=-{\frac {28489}{2160}},C_{4}={\frac {7891}{432}},C_{5}=-{\frac {4355}{432}}$

Implemented Characteristic

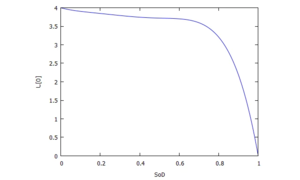
The plot right shows the resultant characteristic of e(S_D):

For the remaining parameters, no measurements were available. We adopted those to obtain a performance similar to what has been described in [1], the resistors were chosen as to “deliver” reasonable amounts of heat when the battery is discharged with rating of C=25.

• R₁ = 500 mΩ
• R₂ = 250 mΩ
• C = 500 F
• Q_B0 = 5000 Ah
• T₀ = 20°C

For α and β we know that their gradients

${\frac {\displaystyle d\;\alpha }{\displaystyle d\;I_{B}}}>0$

and

${\frac {\displaystyle d\;\beta }{\displaystyle \;dT}}<0$.

The reference curve from above shall be assumed to be valid for I_B = 20 A and we assume

${\begin{array}{lll}\alpha (I_{B})&=1+{\frac {\displaystyle I_{B}}{\displaystyle I_{\alpha }}}&{\text{ with }}I_{\alpha }=100A\\\beta (T)&=1-{\frac {\displaystyle T_{B}}{\displaystyle T_{\beta }}}&{\text{ with }}T_{\beta }=100^{\circ }C\end{array}}$

Then, for the thermal model we have

• m_B = 340 g,
• c_p,B = 2 J/(kg K).

And finally h_B will be identified from a (virtual) experiment: let I_B = 0, I₂=0 (no heat generation) and the initial battery-temperature to be ΔT(0) above T₀. Then assume that ΔT(3min) is reduced to 50% of ΔT(0). From above, we find the differential equation to be

$\Delta T(t)=\Delta T_{0}\cdot {\text{e}}^{-{\frac {\displaystyle h_{B}\cdot t}{\displaystyle m_{B}\cdot c_{PB}}}}$,

thus for this “experiment”

$h_{B}=({\text{log}}(2)\cdot m_{B}\cdot c_{PB})/3{\text{ min}}$.

With the values given above, we find

h_B=2.6E-3 J/(Ks)

Let the tolerable, maximum battery temperature be

$T_{B,max}=60^{\circ }C$.

---

next workpackage: car-body →

References

1. Lijun Gao, Shengyi Liu; Roger A. Dougal: Dynamic Lithium-Ion Battery Model for System Simulation, IEEE TRANSACTIONS ON COMPONENTS AND PACKAGING TECHNOLOGIES, VOL. 25, NO. 3, SEPTEMBER 2002 pp. 495
2. P. Villano, M. Carewska, S. Passerini: Specific heat capacity of lithium polymer battery components; Elsevier, Thermochimica Acta 402 (2003) 219–224