Gelöste Aufgaben/JUMP/E-Motor and Drive-Train

← Back to Start

Scope

Diagram of drive-train components.

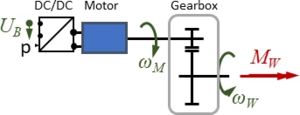
The Drive-Train consists of a DC/DC-converter, a DC Motor and a gear-box.

• DC/DC-converter: is supplied with the battery voltage U_B, the output voltage is controlled by the driver via setpoint “p“.
• motor: is a standard DC brushed motor, the manufacturer provides only few information on its characteristics - we’ll need to improvise.
• gearbox: has a gear ratio of ratio of n_G=100, its shaft rotates at speed ω_W and delivers a torque M_W to the front wheels.

The task is: provide a mathematical model for the drive train that accounts for load-alterations imposed by the driver. And we assume losses in the two converters - DC/DC and gearbox - to be negligible.

Structure

Block diagram

The drive train receives a "gas"-pedal position "p" from the driver and a battery-voltage U_B.

It delivers a torque M_W on the wheel and creates an electric current I_M through the motor.

Drive-train components.

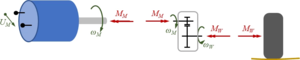
The sub-model consists of  DC/DC-converter, Motor and gear-box:

DC/DC Converter

Losses in the DC/DC converter shall be small - so for input port “1“ and output port “2“ we obtain

$U_1\cdot I_1=U_2\cdot I_2$ .

Let the “gas”-pedal-indicator “p“ control

$U_2=p\cdot U_1\text{; }0\le p\le 1.$

with

$0\le p\le 1\text{ and }{U}_1=U_B$

Motor

Brushed-DC motor

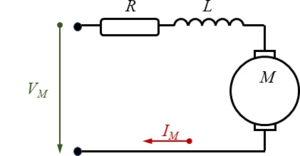
We use a common electric circuit representation for a series wound motor, the field coils are connected electrically in series with the armature coils, resistance R sums up all electrical losses in the motor.

Gearbox

Losses in the gearbox shall be small - so for input (ω_M, M_M) and output (ω_W, M_W) we obtain the fixed relation

${\omega }_M\cdot M_M={\omega }_W\cdot M_W$.

And we have only one differential equation for the electrical components:

$\frac{d{I}_B}{dt}=\frac{U_L}{L}$,

the remaining equations are algebraic.

Model

Electrical Components

For the motor, we find with Kirchhoff's law that

$U_M=U_R+U_L+e$

with U_R, U_L being the differential voltage over resistance R and inductance L respectively. “e” is the back electromagnetic force with

$e=k_e\cdot {\omega }_M$

and the electromotive force constant k_e. Note the ω_M is the differential rotational velocity between rotor and stator, i.e.

${\omega }_M={\dot{\psi }}_W(t)+\dot{\varphi }(t).$

Employing

$U_R=R\cdot I_M,U_L=L\cdot \frac{d{I}_M}{dt}$

and using

$M_M=k_t\cdot I_M$

with the armature constant k_t, we have the complete set of equations.

From the above, we find

$L\cdot \frac{d}{dt}{I}_M(t)=U_B(t)\cdot p(t)-R{I}_M(t)-e$

and additionally the algebraic equations

$\begin{array}{ll}{I}_B& =I_M\cdot \mathrm{p}(t),\\ U_R& =R\cdot I_M(t),\\ U_L& =U_B\cdot \mathrm{p}(t)-R\cdot I_M(t)-e,\\ U_M& =U_B\cdot \mathrm{p}(t)\end{array}$.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 16.04.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2021-02-08                            */
/* ref: Modelling and Simulation (TUAS)                */
/* description: virtual work of drive train electrics  */
/*******************************************************/

/*******************************************************/
/* declarations                                        */
/*******************************************************/
declare("φ", alphabetic);
declare("ψ", alphabetic);
declare("ω", alphabetic);

/*******************************************************/
/* kinematics                                          */
/*******************************************************/
kirchhoff : [U[M] = p(t)*U[B],
	     U[B]*I[B] = U[M]*I[M],
	     U[M] = U[R] + U[L] + e,
             e = k[e]*omega[M],
	     ω[M] = diff(ψ[M](t),t)+diff(φ(t),t),
	     U[R] = R*I[M](t),
	     U[L] = L * diff(I[M](t),t),
	     M[M] = k[t]*I[M](t)];

solve(kirchhoff[7], [diff(I[M](t),t)]);

Mechanical Components

The Virtual Work of d'Alembert forces, motor torque M_M and wheel torque M_W is

$\begin{array}{ll}\delta W& =-J_M\cdot {\ddot{\psi }}_M(t)\cdot \delta {\psi }_M+M_M\cdot ({\psi }_M+\varphi (t))-M_W\cdot \delta {\psi }_W\\ & =0\end{array}$.

Since the gearbox is built into the car, the wheel-side relative gear-box-angle is

${\tilde{\psi }}_W={\psi }_W(t)-\varphi (t)$

and on the motor-side

${\tilde{\psi }}_M={\psi }_M(t)+\varphi (t)$.

With the gear transmission ratio

$n_G=\frac{{\tilde{\psi }}_M}{{\tilde{\psi }}_W}$

and

${\underset{\_}{q}}_E=\left(\begin{array}{c}\varphi (t)\\ {\psi }_W(t)\end{array}\right)$

we find

$\delta W=\delta {\underset{\_}{q}}_E\cdot (-{\underset{\_}{\underset{\_}{M}}}_E\cdot {\underset{\_}{\ddot{q}}}_E+\left(\begin{array}{c}-n_G\cdot M_M\\ +n_G\cdot M_M-M_W\\ \end{array}\right))$

with

${\underset{\_}{\underset{\_}{M}}}_E=\left(\begin{array}{cc}(n_G^2+2n_G+1)J_M& -(n_G^2+n_G)J_M\\ -(n_G^2+n_G)J_M& n_G^2{J}_M\end{array}\right)$.

We have thus "returned" all state variables to the Car-Body-submodel.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 16.04.2                           */
/* author: Andreas Baumgart                            */
/* last updated: 2021-02-08                            */
/* ref: Modelling and Simulation (TUAS)                */
/* description: virtual work of drive train mechanics  */
/*******************************************************/

/*******************************************************/
/* declarations                                        */
/*******************************************************/
declare("δ", alphabetic);
declare("φ", alphabetic);
declare("ψ", alphabetic);

/*******************************************************/
/* kinematics                                          */
/*******************************************************/
kin : [ψ[M,r] = n[G]*ψ[W,r],
       ψ[W,r] = ψ[W](t) - φ(t),
       ψ[M,r] = ψ[M](t) + φ(t)];
Q : [ψ[M](t),ψ[M,r],ψ[W,r]];
sol: ratsimp(solve(kin,Q))[1];


/* Principle of Virtual Work */
PVW: δW = - J[M]*diff(ψ[M](t),t,2)*δψ[M] + M[M]*(δψ[M]+δφ) - M[W]*δψ[W];

/* minimal coordinates */
q : [ φ(t), ψ[W](t)];
δq: [δφ   ,δψ[W]   ];

varia: [ψ[M](t)=δψ[M],ψ[M,r]=δψ[M,r],ψ[W,r]=δψ[W,r],
        ψ[W](t)=δψ[W], φ(t) =δφ];
sol : expand(append(sol, subst(varia,sol)));

PVW : expand(subst(sol,PVW));
PVW : ev(PVW,nouns);

eom : makelist(coeff(rhs(PVW),δq[i]),i,1,2);
eom : ratsimp(eom);

MM : funmake('matrix,makelist(makelist(ratsimp(coeff(-eom[i],'diff(q[j],t,2))),j,1,2),i,1,2));

rest : expand(eom + makelist(sum(MM[i,j]*diff(q[j],t,2),j,1,2),i,1,2));

print(δq, "*(-",MM,"*",transpose(diff(q,t,2)),"+",transpose(rest),") = 0")$

Consequently, the drive train has only one state-variable: I_M:

${\underset{\_}{q}}_E(t)=(I_M(t))$

where

$\frac{d}{dt}{I}_M(t)=\frac{U_B\mathrm{p}(t)-R{I}_M(t)-e}{L}$

and with this algebraic equation

$e=k_e\cdot ({\dot{\psi }}_W(t)+\dot{\varphi }(t))$.

Variables

name	symbol	unit
motor current	IM	A

Parameter

System parameters for the motor are k_T / k_e and R_M . For the stationary ($\frac{d{I}_M}{dt}=0$) - condition, we derive

$M_M=\frac{U_M{k}_T-k_T{k}_e{\omega }_M}{R_M}$,

so that we see:

1. under a "no-load"-condition M_M=0, we have

${\omega }_{NL}=\frac{U_M}{k_e}$

1. under the "stalled motor"-condition ω_St=0, we have

$M_{St}=\frac{k_T\cdot U_M}{R_M}$

Thus we can replace k_T / k_e, R_M by ω_NL and M_St, which make the system parameters to be selected more descriptive.

name	symbol	value	unit
no-load rotational speed	ωNL	1	rad/s
stall-torque	MSt	2	N m
inductance	L	3	H
gear tramission ratio	nG	4	1

Back to Start →

---

References

• ...