Gelöste Aufgaben/JUMP/Car-Body: Unterschied zwischen den Versionen
| Zeile 83: | Zeile 83: | ||
==tmp== | ==tmp== | ||
[[Datei:JUMP-track-slide8.png|mini|Tack specification]]We describe the road by road-sections, which we call tracks. We start by defining each track as a line-segment, i.e. a first-order polynomial. The road is thus defined by pairs of track-endpoints, i.e. (''x<sub>i</sub>'', ''y<sub>i</sub>''). | |||
The track-polynomials are | |||
<math>\begin{array}{ll} | |||
t_i(x) &= y_i \cdot \tilde{x}_i + y_{i-1}\cdot \left(1- \tilde{x}_i \right) \text{ for } \tilde{x}_i = \frac{\displaystyle x - x_{i-1}}{\displaystyle x_i - x_{i-1}}\\ | |||
&=T_{i,1}\cdot x + T_{i,0} | |||
\end{array}</math>. | |||
During the numerical integration of the initial-value-problem - when the car runs along the track - the solver needs to cope with the transition between two straight lines - which is numerically more efficient if we convert the road in a continuously differentiable function. [[Datei:JUMP-carbody-track-rounding.png|mini|Rounding the edges.]]For this purpose, we define transition polynomials ''p<sub>i</sub>'' of second degree - parabolas - as | |||
<math>p_i(x) = \displaystyle \sum_{j=0}^2 P_{i,j}\cdot x^j</math> | |||
which connect two neighboring tracks. | |||
The boundary conditions for the parabolas (red) and the neighboring lines (blue) yield | |||
<math>\begin{array}{ll} | |||
\color{blue} t_i(x_i-\Delta x_i) &= \color{red} p_{i}(x_i-\Delta x_i),\\ | |||
\color{blue} | |||
\left.\frac{\displaystyle d t_i}{\displaystyle d x_i}\right\vert_{x_i-\Delta x_i} | |||
&= \color{red} | |||
\left.\frac{\displaystyle d p_i}{\displaystyle d x_i}\right\vert_{x_i-\Delta x_i},\\ | |||
\color{blue} t_{i+1}(x_i+\Delta x_i) &= \color{red} p_{i}(x_i+\Delta x_i),\\ | |||
\color{blue} | |||
\left.\frac{\displaystyle d t_{i+1}}{\displaystyle d x_{i+1}}\right\vert_{x_i+\Delta x_i} | |||
&= \color{red} | |||
\left.\frac{\displaystyle d p_i}{\displaystyle d x_i}\right\vert_{x_i+\Delta x_i}. | |||
\end{array}</math> | |||
And though we have four boundary conditions, they allow for a solution with three unknown polynomial coefficients ''P<sub>i</sub>'' if ''Δx<sub>i</sub>'' is identical left and right from ''x<sub>i</sub>'' - which we have already implied. | |||
<math>\begin{array}{ll} | |||
{b_3}&=0,\\ | |||
{b_2}&=\frac{\displaystyle {a_{2,1}}-{a_{1,1}}}{\displaystyle 4 \mathit{\Delta x_i}},\\ | |||
{b_1}&=\frac{\displaystyle \left( {a_{2,1}}+{a_{1,1}}\right) \, \mathit{\Delta x_i}-{x_i}\, {a_{2,1}}+{x_i}\, {a_{1,1}}}{\displaystyle 2 \mathit{\Delta x_i}},\\ | |||
{b_0}&=\frac{\displaystyle \left( {a_{2,1}}-{a_{1,1}}\right) \, {{\mathit{\Delta x_i}}^{2}}+\left( -2 {x_i}\, {a_{2,1}}-2 {x_1}\, {a_{1,1}}+4 {y_i}\right) \, \mathit{\Delta x_i}+{{x}_{i}^{2}}\, {a_{2,1}}-{{x}_{i}^{2}}\, {a_{1,1}}}{\displaystyle 4 \mathit{\Delta x_i}} | |||
\end{array}</math> | |||
and | |||
<math>\begin{array}{ll} | |||
{a_{1,0}}&={y_i}-{x_i}\, {a_{1,1}},\\ | |||
{a_{1,1}}&=\frac{\displaystyle {y_{i-1}}-{y_i}}{\displaystyle {x_{i-1}}-{x_i}}\operatorname{,}\\ | |||
{a_{2,0}}&={y_i}-{x_i}\, {a_{2,1}},\\ | |||
{a_{2,1}}&=\frac{\displaystyle {y_i}-{y_{i+1}}}{\displaystyle {x_i}-{x_{i+1}}} | |||
\end{array}</math> | |||
But instead of employing the above, we solve the linear systems of equations for the coefficients numerically. | |||
Now each polynomial creates new endpoints ''x<sub>i</sub>'' - ''Δx<sub>i</sub>'' and ''x<sub>i</sub>'' + ''Δx<sub>i</sub>'' which substitute for the initial ''x<sub>i</sub>''-point. The tracks are represented by a succession of lines and parabolas. | |||
{{MyCodeBlock | {{MyCodeBlock | ||
|title=Track | |title=Track | ||
| Zeile 168: | Zeile 222: | ||
z | z | ||
a | a | ||
b | b | ||
[[Datei:JUMP-carbody-slide5.png|mini|Contact conditions.]] | [[Datei:JUMP-carbody-slide5.png|mini|Contact conditions.]] | ||
Version vom 10. März 2021, 12:51 Uhr
Scope
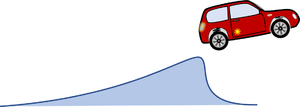
In common simulation applications - especially for full-size commercial cars - the pitch-angle of the car is assumed to be small to allow for a linearization of geometry and most parts of the equations of motion. We drop this limitation so we can do more fancy stuff with our model - like climbing steep roads or jumping across ditches.
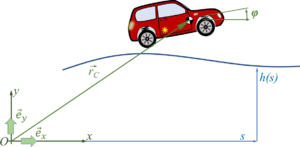
We employ a spatial x-y coordinate system, x in horizontal, y in vertical, upwards direction. And we’ll briefly employ the z-axis as rotation direction - which is towards you following the “right-hand-rule“ for coordinate systems.
Structure
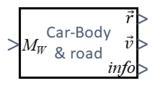
The driver controls the car's motion via the position of the "gas"-pedal, which is being translated into a torque MW at the wheel.
This toque will change velocities and thus the position of the car. These state-variables will then create - via info - a feedback to the driver.
We’ll need to invest significant efforts in describing the kinematics of the car-motion and to derive its equations of body-motion since we do not want to limit our study on small pitch-angles of the car. Key accessory will be vectors, which map locations like the center of mass:
- .
This vector has - in 2D - two coordinates , measured in the inertial x-y frame:
- with .
representing the unit vectors spanning the x-y space. If we refer to a specific frame, we may drop the vector-notation and refer to the column-matrix of coordinates only, so
- .
We’ll also employ coordinate transformations using Euler-rotations.
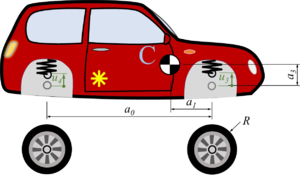
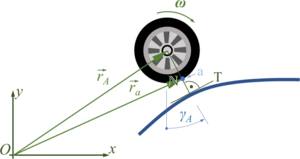
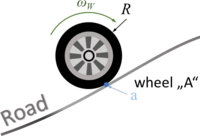
The car with front-wheel drive consists of the car-body with center of mass “C“, the front wheels “A“ and the rear wheel “B“. Masses of car-body and wheel-sets are M and m respectively.The geometry of the car is described by
- a0: the wheel base;
- a1: longitudinal distance between center of mass and front-wheel-hub;
- a2 = a0 - a1 and
- a3: vertical distance between center of mass and front-wheel-hub (relaxed springs).
tmp
Body
We use five coordinates to describe the motion of the car:
- for the location of the center of mass of the car-body and its pitch-angle
 ,
, - for the "vertical" motion of the wheel hubs relative to the car-body - which is synonym to the compression of the springs
and - as the rotation angle of the front-wheel - we'll not account for the rotation of the rear-wheel.
So the center of mass of the car-body is
- ,
the coordinate system of the car is
where
- .
So the location of the front-wheel “A“ is
or
- .
Likewise, the location of the rear-wheel “B“ is
and in the following, we’ll be using the abbreviations
and
- .
tmp
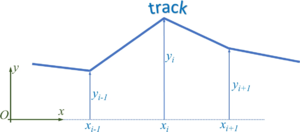
We describe the road by road-sections, which we call tracks. We start by defining each track as a line-segment, i.e. a first-order polynomial. The road is thus defined by pairs of track-endpoints, i.e. (xi, yi).
The track-polynomials are
.
During the numerical integration of the initial-value-problem - when the car runs along the track - the solver needs to cope with the transition between two straight lines - which is numerically more efficient if we convert the road in a continuously differentiable function.
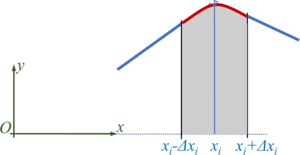
For this purpose, we define transition polynomials pi of second degree - parabolas - as
which connect two neighboring tracks.
The boundary conditions for the parabolas (red) and the neighboring lines (blue) yield
And though we have four boundary conditions, they allow for a solution with three unknown polynomial coefficients Pi if Δxi is identical left and right from xi - which we have already implied.
and
But instead of employing the above, we solve the linear systems of equations for the coefficients numerically.
Now each polynomial creates new endpoints xi - Δxi and xi + Δxi which substitute for the initial xi-point. The tracks are represented by a succession of lines and parabolas.
Track
Text
1+1=2
tmp
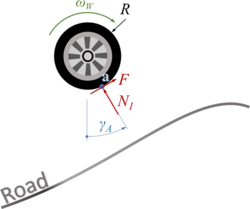
Contact-Point and -Normal
Text
1+1=2
tmp
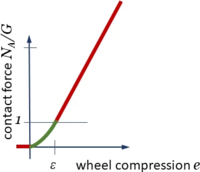
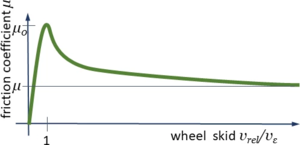
Contact Forces
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
tmp
Track
Text
1+1=2
Variables
Parameter
x
y
z
a
b
c
next workpackage: driver-controls →
References
- ...