Gelöste Aufgaben/JUMP/Car-Body: Unterschied zwischen den Versionen
| Zeile 2: | Zeile 2: | ||
==Scope== | ==Scope== | ||
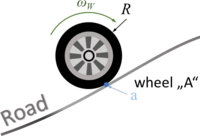
[[Datei:JUMP-01.png|mini|Car-Body]] | [[Datei:JUMP-01.png|mini|Car-Body]]In common simulation applications - especially for full-size commercial cars - the pitch-angle of the car is assumed to be small to allow for a linearization of geometry and most parts of the equations of motion. We drop this limitation so we can do more fancy stuff with our model - like climbing steep roads or jumping across ditches.[[Datei:JUMP-carbody-block-diagram.png|mini|Block Diagram.|alternativtext=|ohne|155x155px]]We employ a spatial x-y coordinate system, ''x'' in horizontal, ''y'' in vertical, upwards direction. And we’ll briefly employ the z-axis as rotation direction - which is towards you following the “right-hand-rule“ for coordinate systems. | ||
==Structure== | ==Structure== | ||
The driver controls the car's motion via the position of the "gas"-pedal, which is being translated into a torque ''M<sub>W</sub>'' at the wheel. | |||
This toque will change velocities and thus the position of the car. These state-variables will then create - via ''info'' - a feedback to the driver. | |||
We’ll need to invest significant efforts in describing the kinematics of the car-motion and to derive its equations of body-motion since we do not want to limit our study on small pitch-angles of the car. Key accessory will be [[Sources/Lexikon/Vektor|vectors]], which map locations like the center of mass: | |||
<math>\vec{r}_C(t)</math>. | |||
This vector has - in 2D - two coordinates <math>u_1(t), u_2(t)</math>, measured in the inertial ''x-y'' frame: | |||
<math>\vec{r}_C(t) = \vec{\underline{e}}_0 \cdot \left(\begin{array}{c} u_1\\u_2\end{array}\right)</math> with <math>\vec{\underline{e}}_0 = \left(\vec{e}_x, \vec{e}_y \right)</math>. | |||
representing the unit vectors spanning the ''x-y'' space. If we refer to a specific frame, we may drop the vector-notation <math>(\vec{.})</math> and refer to the column-matrix of coordinates <math>(\underline{.})</math> only, so | |||
<math>\underline{r}_C = \left( \begin{array}{c}u_1\\u_2\end{array}\right)</math>. | |||
We’ll also employ coordinate transformations using [[Sources/Lexikon/Euler-Rotation|Euler-rotations]]. | |||
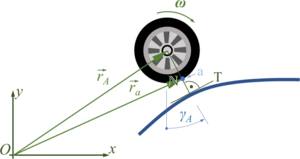
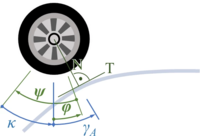
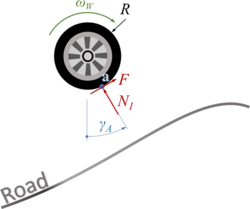
The car with front-wheel drive consists of the car-body with center of mass “''C''“, the front wheels “''A''“ and the rear wheel “''B''“. Masses of car-body and wheel-sets are ''M'' and ''m'' respectively.The geometry of the car is described by | |||
* ''a<sub>0</sub>'': the wheel base; | |||
* ''a<sub>1</sub>'': longitudinal distance between center of mass and front-wheel-hub; | |||
* ''a<sub>2</sub> = a<sub>0</sub> - a<sub>1</sub>'' and | |||
* ''a<sub>3</sub>'': vertical distance between center of mass and front-wheel-hub (relaxed springs). | |||
==Model== | ==Model== | ||
| Zeile 11: | Zeile 35: | ||
==Parameter== | ==Parameter== | ||
x | x | ||
[[Datei:JUMP-carbody-slide3.png|mini|Body Coordinates]] | [[Datei:JUMP-carbody-slide3.png|mini|Body Coordinates]] | ||
Version vom 10. März 2021, 10:54 Uhr
Scope
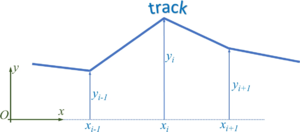
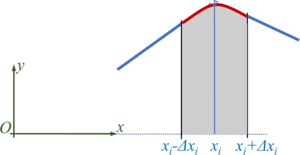
In common simulation applications - especially for full-size commercial cars - the pitch-angle of the car is assumed to be small to allow for a linearization of geometry and most parts of the equations of motion. We drop this limitation so we can do more fancy stuff with our model - like climbing steep roads or jumping across ditches.
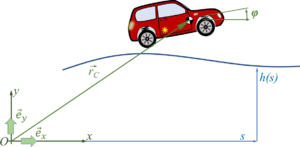
We employ a spatial x-y coordinate system, x in horizontal, y in vertical, upwards direction. And we’ll briefly employ the z-axis as rotation direction - which is towards you following the “right-hand-rule“ for coordinate systems.
Structure
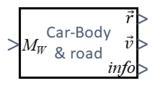
The driver controls the car's motion via the position of the "gas"-pedal, which is being translated into a torque MW at the wheel.
This toque will change velocities and thus the position of the car. These state-variables will then create - via info - a feedback to the driver.
We’ll need to invest significant efforts in describing the kinematics of the car-motion and to derive its equations of body-motion since we do not want to limit our study on small pitch-angles of the car. Key accessory will be vectors, which map locations like the center of mass:
.
This vector has - in 2D - two coordinates , measured in the inertial x-y frame:
with .
representing the unit vectors spanning the x-y space. If we refer to a specific frame, we may drop the vector-notation and refer to the column-matrix of coordinates only, so
.
We’ll also employ coordinate transformations using Euler-rotations.
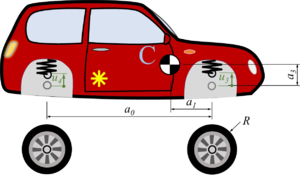
The car with front-wheel drive consists of the car-body with center of mass “C“, the front wheels “A“ and the rear wheel “B“. Masses of car-body and wheel-sets are M and m respectively.The geometry of the car is described by
- a0: the wheel base;
- a1: longitudinal distance between center of mass and front-wheel-hub;
- a2 = a0 - a1 and
- a3: vertical distance between center of mass and front-wheel-hub (relaxed springs).
Model
Variables
Parameter
x
y
z
a
b
c
next workpackage: driver-controls →
References
- ...