Gelöste Aufgaben/FEB2: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 10: | Zeile 10: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
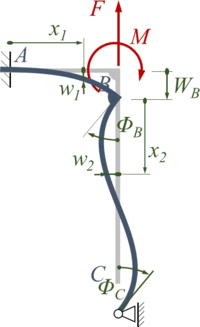
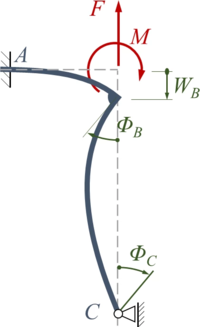
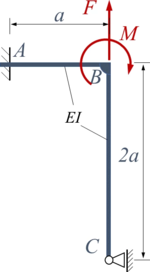
Die zwei Euler-Bernoulli-Balken ''AB'' (Länge ''a'') und ''BC'' (Länge ''2a'') sind in ''B'' fest verschweißt. Ihre Biegesteifigkeit ist ''EI''. Die Konstruktion ist in ''A'' fest eingespannt und in ''C'' durch ein verschiebliches Gelenklager gelagert. In ''B'' ist sie durch die Kraft ''F'' und das Moment ''M'' belastet. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:FEB2-01.png|mini|272x272px|Lageplan]] | [[Datei:FEB2-01.png|mini|272x272px|Lageplan]] | ||
Gesucht ist | Gesucht ist die Verschiebungen und Verdrehungen der Balken mit der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten ELemente]]. | ||
</onlyinclude> | </onlyinclude> | ||
Gegeben: ''a, E I, F, M'' | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
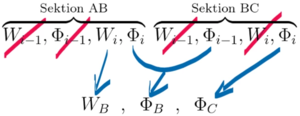
Berechnet werden sollten daf[r die Auslenkungen und Verdrehung der Punkte ''A, B'' und ''C''. Das Modell soll aus zwei Finiten Elementen bestehen, jeweils eins für den Abschnitt ''AB'' und ''BC''. Die neutralen Fasern der beiden Balken seien in Längsrichtung undehnbar – die Querschnitts-Schwerpunkte verschieben sich also nicht in Balken-Längsrichtung. | |||
<!--------------------------------------------------------------------------------> | ))tmp)) | ||
{{MyCodeBlock|title= | <!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | ||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
))tmp)) | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
))tmp)) | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Coordinates | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
))tmp)) | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Assembly of System Matrices | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
))tmp)) | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
))tmp)) | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post/Processing | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
Version vom 25. Februar 2021, 14:52 Uhr
Aufgabenstellung
Die zwei Euler-Bernoulli-Balken AB (Länge a) und BC (Länge 2a) sind in B fest verschweißt. Ihre Biegesteifigkeit ist EI. Die Konstruktion ist in A fest eingespannt und in C durch ein verschiebliches Gelenklager gelagert. In B ist sie durch die Kraft F und das Moment M belastet.
Gesucht ist die Verschiebungen und Verdrehungen der Balken mit der Methode der Finiten ELemente.
Gegeben: a, E I, F, M
Lösung mit Maxima
Berechnet werden sollten daf[r die Auslenkungen und Verdrehung der Punkte A, B und C. Das Modell soll aus zwei Finiten Elementen bestehen, jeweils eins für den Abschnitt AB und BC. Die neutralen Fasern der beiden Balken seien in Längsrichtung undehnbar – die Querschnitts-Schwerpunkte verschieben sich also nicht in Balken-Längsrichtung.
))tmp))
Header
Text
1+1
))tmp))
Declarations
Text
1+1
))tmp))
Coordinates
Text
1+1
))tmp))
Assembly of System Matrices
Text
1+1
))tmp))
Solving
Text
1+1
))tmp))
Post/Processing
Text
1+1
Links
- ...
Literature
- ...