Gelöste Aufgaben/COVI: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 37: | Zeile 37: | ||
== Lösung mit Matlab == | == Lösung mit Matlab == | ||
{{MyCodeBlock|title=Header|text= | {{MyCodeBlock|title=Header|text=Wt.|code= | ||
<syntaxhighlight lang="matlab" line start=1> | |||
<syntaxhighlight lang="matlab"> | |||
%******************************************************* | %******************************************************* | ||
%* matlab script * | %* matlab script * | ||
| Zeile 52: | Zeile 51: | ||
}} | }} | ||
{{MyCodeBlock|title=Declarations|text=Wir | {{MyCodeBlock|title=Declarations|text=Wir verwenden diese Parameter aus einer Tabelle | ||
<syntaxhighlight lang="matlab"> | und erklären unten, wie wir sie einsetzten.|code= | ||
<syntaxhighlight lang="matlab" line start=1> | |||
cd 'C:\Users\abs384\OneDrive\Confluence Sources\COVI' | |||
addpath('.\functions') | |||
% | % load parameters | ||
parameter = readtable('parameter.xlsx'); | |||
for row=1:length(parameter.name) | |||
eval(strcat(char(parameter.name(row)),'=', num2str(parameter.zahl(row)))) | |||
end | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
{{MyCodeBlock|title=Equations of Motion|text= | {{MyCodeBlock|title=Equations of Motion|text=W.|code= | ||
<syntaxhighlight lang="matlab" line start=1> | |||
<syntaxhighlight lang="matlab"> | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 86: | Zeile 75: | ||
text=.| | text=.| | ||
code= | code= | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab" line start=1> | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
| Zeile 93: | Zeile 82: | ||
text=.| | text=.| | ||
code= | code= | ||
<syntaxhighlight lang="matlab"> | <syntaxhighlight lang="matlab" line start=1> | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
Version vom 16. Februar 2021, 09:17 Uhr
Aufgabenstellung
Als Ingenieure können wir die COVID-19-Epidemie genauso modellieren, wie technische Systeme.
Wir brauchen dazu "Koordinaten" - also Messgrößen - die die Anzahl der Individuen erfassen, die
- ansteckbar "a",
- infiziert "i" - mit und ohne Sympthome - und
- genesen "r"
sind. Für jede dieser Koordinaten müssen wir nun "Bewegungsgleichungen" - also z.B. Differentialbeziehungen in der Zeit - hinschreiben.
Das nennen wir "Modellbildung".
| 🧨 Dies ist kein zuverlässiges Prognosewerkzweug: |
Hier geht es um die Modellierung
|
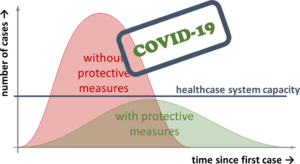
Diese algebraischen und Differentialgleichungen sind dabei nicht das Ergebnis von Gleichgewichtsbeziehungen wie in der Technischen Mechanik. Wir begnügen uns statt dessen damit, Phänomene der Epidemie mit unserer Mathematik zu erfassen.
Und so gehen wir vor:
Wir modellieren eine Grundgesamtheit von n0 = 80 Millionen Individuen.
Die Pandemie soll bei einer Durchseuchung von α=50% zum Stillstand kommen - die Individuen sind dann so weit voneinander entfernt, dass eine Ansteckung unwahrscheinlich ist.
Zum Zeitpunkt t0=0 seien von insgesamt i0 Individuen mit
infiziert.
Lösung mit Matlab
Header
Wt.
%*******************************************************
%* matlab script *
%* version: R2020a *
%* author: Andreas Baumgart *
%* last updated: 2020-03-25 *
%* ref: Technische Mechanik mit Computer *
%* description: COVID-19 Simulation *
%* no spatial resoultion *
%*******************************************************
Declarations
Wir verwenden diese Parameter aus einer Tabelle
und erklären unten, wie wir sie einsetzten.
cd 'C:\Users\abs384\OneDrive\Confluence Sources\COVI'
addpath('.\functions')
% load parameters
parameter = readtable('parameter.xlsx');
for row=1:length(parameter.name)
eval(strcat(char(parameter.name(row)),'=', num2str(parameter.zahl(row))))
end
Equations of Motion
W.
Solving
.
Postprocessing
.