Gelöste Aufgaben/FEB1: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
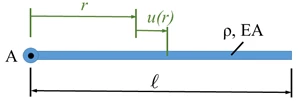
Lageplan
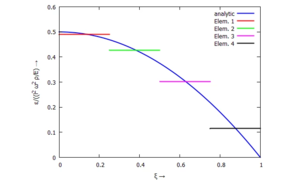
Dehnung ε(x). 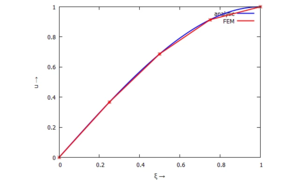
Auslenkung u(x).
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:A*x=b]][[Category:Lineare Algebra]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Prinzip der virtuellen Arbeit]] | |||
[[Category:Dehnstab]] | |||
[[Category:Finite-Elemente-Methode]] | |||
[[Category:Maxima]] | |||
[[Category:Statik]] | |||
==Aufgabenstellung== | |||
Auch wenn es nicht so aussieht: für das rotierende Rotorblatt suchen wir eine statische Lösung - das Problem heißt "quasistatisch". | |||
<onlyinclude> | |||
[[Datei:FEB1-01.png|mini|Lageplan]] | |||
Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. | |||
Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte. | |||
</onlyinclude> | |||
== Lösung mit Maxima == | |||
Lorem Ipsum .... | |||
==tmp== | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Declarations | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equlibrium Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Boundary Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
[[Datei:FEB1-12.png|mini|Dehnung ε(x).]] | [[Datei:FEB1-12.png|mini|Dehnung ε(x).]] | ||
[[Datei:FEB1-11.png|mini|Auslenkung ''u(x)''.]] | [[Datei:FEB1-11.png|mini|Auslenkung ''u(x)''.]] | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
{{MyTip|title=Konstante Dehnung je Element|text=Was ausschaut wie ein Fehler - nämlich die "Treppenfunktion" für die Dehnung im FE-Modell - ist in Wirklichkeit die Folge unserer linearen Ansatzfunktionen. Diese abgeleitet liefern eine konstante Dehnung je Element.}} | {{MyTip|title=Konstante Dehnung je Element|text=Was ausschaut wie ein Fehler - nämlich die "Treppenfunktion" für die Dehnung im FE-Modell - ist in Wirklichkeit die Folge unserer linearen Ansatzfunktionen. Diese abgeleitet liefern eine konstante Dehnung je Element.}} | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
Version vom 25. Februar 2021, 13:18 Uhr
Aufgabenstellung
Auch wenn es nicht so aussieht: für das rotierende Rotorblatt suchen wir eine statische Lösung - das Problem heißt "quasistatisch".

Ein Hubschrauber-Rotor dreht mir der konstanten Winknelgeschwindigkeit Ω. Das Rotor-Blatt ist aus Aluminium. Gesucht ist die FEM-Lösung für der Verschiebung der Querschnitte und die Dehnung der Querschnitte.
Lösung mit Maxima
Lorem Ipsum ....
tmp
Header
Text
1+1
tmp
Declarations
Text
1+1
tmp
Equlibrium Conditions
Text
1+1
tmp
Boundary Conditions
Text
1+1
tmp
Solving
Text
1+1
tmp


Post-Processing
| ✔ Konstante Dehnung je Element: |
| Was ausschaut wie ein Fehler - nämlich die "Treppenfunktion" für die Dehnung im FE-Modell - ist in Wirklichkeit die Folge unserer linearen Ansatzfunktionen. Diese abgeleitet liefern eine konstante Dehnung je Element. |
1+1
Links
- ...
Literature
- ...