Gelöste Aufgaben/FEAG: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 105: | Zeile 105: | ||
<!-------------------------------------------------------------------------------->{{MyNoncodeBlock|title=Equilibrium Conditions | |||
|text= | |||
<!--------------------------------------------------------------------------------> | |||
Die Gleichgewichtsbedingung mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] setzen sich additiv aus | Die Gleichgewichtsbedingung mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] setzen sich additiv aus | ||
<math>\displaystyle \delta W = \sum_{i=1}^I \left(\delta W^a_i - \delta \Pi_i \right) + \delta W^a_R</math>, | ::<math>\displaystyle \delta W = \sum_{i=1}^I \left(\delta W^a_i - \delta \Pi_i \right) + \delta W^a_R</math>, | ||
zusammen - also den virtuellen Arbeiten je Element zuzüglich von virtuellen Arbeiten am Rand. In unserem Beispiel haben wir allerdings keine eingeprägten, äußeren Lasten am Rand, also ist | zusammen - also den virtuellen Arbeiten je Element zuzüglich von virtuellen Arbeiten am Rand. In unserem Beispiel haben wir allerdings keine eingeprägten, äußeren Lasten am Rand, also ist | ||
<math>\delta W^a_R = 0</math>. | ::<math>\delta W^a_R = 0</math>. | ||
Je Element erfassen wir die virtuellen Arbeiten durch Element-Matrizen. So ist z.B. für die virtuelle Formänderungsenergie (vgl. [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]) | Je Element erfassen wir die virtuellen Arbeiten durch Element-Matrizen. So ist z.B. für die virtuelle Formänderungsenergie (vgl. [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]]) | ||
<math>\delta \Pi_i = \left(\delta W_{i-1}, \delta \Phi_{i-1}, \delta W_{i} , \delta \Phi_{i}\right) \cdot \underline{\underline{K}}_i\cdot \left(\begin{array}{c}W_{i-1}(t)\\\Phi_{i-1}(t)\\W_{i}(t)\\\Phi_{i}(t) \end{array}\right)</math> | ::<math>\delta \Pi_i = \left(\delta W_{i-1}, \delta \Phi_{i-1}, \delta W_{i} , \delta \Phi_{i}\right) \cdot \underline{\underline{K}}_i\cdot \left(\begin{array}{c}W_{i-1}(t)\\\Phi_{i-1}(t)\\W_{i}(t)\\\Phi_{i}(t) \end{array}\right)</math> | ||
mit der Element-Steifigkeitsmatrix <math>\underline{\underline{K}}_i</math>. | mit der Element-Steifigkeitsmatrix <math>\underline{\underline{K}}_i</math>. | ||
| Zeile 126: | Zeile 123: | ||
Aus der [[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]] könnten wir die Element-Matrizen der virtuellen Arbeit der [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'schen Trägheitskraft]] sowie der [[Sources/Lexikon/Virtuelle Formänderungsenergie|Virtuelle Formänderungsenergie]] herauskopieren. Auch die "rechte Seite" mit der virtuelle Arbeit der Gewichtskraft aus | Aus der [[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]] könnten wir die Element-Matrizen der virtuellen Arbeit der [[Sources/Lexikon/D'Alembert'sche Trägheitskraft|D'Alembert'schen Trägheitskraft]] sowie der [[Sources/Lexikon/Virtuelle Formänderungsenergie|Virtuelle Formänderungsenergie]] herauskopieren. Auch die "rechte Seite" mit der virtuelle Arbeit der Gewichtskraft aus | ||
<math>\displaystyle \delta W^{a,g}_i = \int_{\ell_i} \varrho\; A \; g \cdot \delta w(x) \;dx_i</math>, | ::<math>\displaystyle \delta W^{a,g}_i = \int_{\ell_i} \varrho\; A \; g \cdot \delta w(x) \;dx_i</math>, | ||
könnten wir als Element-Lastmatrix (Spaltenmatrix) abspeichern. | könnten wir als Element-Lastmatrix (Spaltenmatrix) abspeichern. | ||
<math>\displaystyle \underline{G}_i = \frac{\varrho\,A\, g\, \ell_i}{2} \cdot \left(\begin{array}{c}+1\\\displaystyle +\frac{\ell_i}{6}\\+1\\\displaystyle -\frac{\ell_i}{6}\end{array}\right)</math>. | ::<math>\displaystyle \underline{G}_i = \frac{\varrho\,A\, g\, \ell_i}{2} \cdot \left(\begin{array}{c}+1\\\displaystyle +\frac{\ell_i}{6}\\+1\\\displaystyle -\frac{\ell_i}{6}\end{array}\right)</math>. | ||
Dass es auch anders geht,sehen Sie in der Definition der Matlab-Klasse FEM_Element_Modell, bei der die Element direkt aus den Trial-Functions - hier den | Dass es auch anders geht,sehen Sie in der Definition der Matlab-Klasse FEM_Element_Modell, bei der die Element direkt aus den Trial-Functions - hier den | ||
<math>\underline{\tilde{\phi}}</math> - | ::<math>\underline{\tilde{\phi}}</math> - | ||
hergeleitet. werden: | hergeleitet. werden: | ||
<pre> | |||
: | : | ||
K(row,col) = diff(... | K(row,col) = diff(... | ||
| Zeile 146: | Zeile 142: | ||
[0,1])); | [0,1])); | ||
: | : | ||
</pre> | |||
=== Komponieren der System-Matrizen === | |||
Die System-Matrizen des Gesamt–Systems komponieren wir nun durch Hinzuaddieren der Anteile je Element. | Die System-Matrizen des Gesamt–Systems komponieren wir nun durch Hinzuaddieren der Anteile je Element. | ||
Beispiel: die Gesamt-Steifigkeitsmatrix für I=2: | Beispiel: die Gesamt-Steifigkeitsmatrix für I=2: | ||
<math>\displaystyle \underline{\underline{K}} = \frac{E\,I}{\ell_i^3} \cdot \left( \begin{array}{ccccc} | ::<math>\displaystyle \underline{\underline{K}} = \frac{E\,I}{\ell_i^3} \cdot \left( \begin{array}{ccccc} | ||
{\color{red}{+12}}&{\color{red}{+6}}&{\color{red}{-12}}&{\color{red}{+6}}&0&0\\ | {\color{red}{+12}}&{\color{red}{+6}}&{\color{red}{-12}}&{\color{red}{+6}}&0&0\\ | ||
{\color{red}{+6\ell_i}}&{\color{red}{+4\ell_i^2}}&{\color{red}{-6\ell_i}}&{\color{red}{+2\ell_i^2}}&0&0\\ | {\color{red}{+6\ell_i}}&{\color{red}{+4\ell_i^2}}&{\color{red}{-6\ell_i}}&{\color{red}{+2\ell_i^2}}&0&0\\ | ||
| Zeile 165: | Zeile 161: | ||
Dieses "Hinzuaddieren" passiert in [[Gelöste Aufgaben/FEAG/FEAG-Matlab|Matlab]] hier: | Dieses "Hinzuaddieren" passiert in [[Gelöste Aufgaben/FEAG/FEAG-Matlab|Matlab]] hier: | ||
< | <pre> | ||
: | : | ||
e = 0;% counter for all elements of all sections | e = 0;% counter for all elements of all sections | ||
| Zeile 179: | Zeile 175: | ||
end | end | ||
: | : | ||
</ | </pre> | ||
In Matrix-Schreibweise lautet die Bewegungsgleichung des Gesamt-Systems jetzt: | In Matrix-Schreibweise lautet die Bewegungsgleichung des Gesamt-Systems jetzt: | ||
<math>\underline{\underline{M}}\cdot\underline{\ddot{Q}} + \underline{\underline{K}}\cdot\underline{Q} = \underline{G}</math>. | ::<math>\underline{\underline{M}}\cdot\underline{\ddot{Q}} + \underline{\underline{K}}\cdot\underline{Q} = \underline{G}</math>. | ||
=== Einarbeiten der Randbedingungen === | |||
[[Datei:FEAG-11-Randbedingungeneinarbeiten.png|mini|Randbedingungen einarbeiten.]] | [[Datei:FEAG-11-Randbedingungeneinarbeiten.png|mini|Randbedingungen einarbeiten.]] | ||
Die Randbedingungen arbeiten wir ein, indem wir zeilenweise (für ''δW'' und ''δΦ'') und spaltenweise (für ''W'' und ''Φ'') streichen. | Die Randbedingungen arbeiten wir ein, indem wir zeilenweise (für ''δW'' und ''δΦ'') und spaltenweise (für ''W'' und ''Φ'') streichen. | ||
| Zeile 192: | Zeile 188: | ||
* die erste Zeile/Spalte für <span style="color:#000080">''W<sub>0</sub>'' (blau)</span> und | * die erste Zeile/Spalte für <span style="color:#000080">''W<sub>0</sub>'' (blau)</span> und | ||
* die zweite Zeile / Spalte für <span style="color:#008000">''Φ<sub>0</sub>'' (grün)</span>. | * die zweite Zeile / Spalte für <span style="color:#008000">''Φ<sub>0</sub>'' (grün)</span>. | ||
}} | |||
<!-------------------------------------------------------------------------------->{{MyNoncodeBlock|title=Solving | |||
<!-------------------------------------------------------------------------------->Die Lösung des Anfangs- und Randwertproblems ist in diesem Lösungsansatz mit Matlab um die Klasse "FEM_Container" herum aufgebaut - in ihr sind alle Parameter und Lösungsprozesse beschrieben. | |text= | ||
Die Lösung des Anfangs- und Randwertproblems ist in diesem Lösungsansatz mit Matlab um die Klasse "FEM_Container" herum aufgebaut - in ihr sind alle Parameter und Lösungsprozesse beschrieben. | |||
Hier heißt die Instanz des Modells | Hier heißt die Instanz des Modells | ||
| Zeile 209: | Zeile 207: | ||
Die Gesamtlösung ''Q<sub>t</sub>'' setzt sich nun - bei diesem linearen System - additiv aus partikularer ''Q<sub>p</sub>'' und ''Q<sub>h</sub>'' homogener Lösung zusammen: | Die Gesamtlösung ''Q<sub>t</sub>'' setzt sich nun - bei diesem linearen System - additiv aus partikularer ''Q<sub>p</sub>'' und ''Q<sub>h</sub>'' homogener Lösung zusammen: | ||
<math>\underline{Q}_t(t) = \underline{Q}_p(t) + \underline{Q}_h(t)</math> | ::<math>\underline{Q}_t(t) = \underline{Q}_p(t) + \underline{Q}_h(t)</math> | ||
=== Particular Solution === | |||
[[Datei:FEAG-12-particulareLösung.png|mini|Particulare Lösung.]] | [[Datei:FEAG-12-particulareLösung.png|mini|Particulare Lösung.]] | ||
Die rechte Seite der Bewegungsgleichung ''G'' ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung ''Q<sub>p</sub>'' statisch, wir suchen nach der Lösung des Gleichungssystems | Die rechte Seite der Bewegungsgleichung ''G'' ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung ''Q<sub>p</sub>'' statisch, wir suchen nach der Lösung des Gleichungssystems | ||
| Zeile 263: | Zeile 261: | ||
Acht Eigenwerte kommen aus der Bedingung <math>\det(\underline{\underline{D}})=0</math>, diese <math>\Lambda_i</math> werden auf der Spur der Matrix D abgelegt: | Acht Eigenwerte kommen aus der Bedingung <math>\det(\underline{\underline{D}})=0</math>, diese <math>\Lambda_i</math> werden auf der Spur der Matrix D abgelegt: | ||
< | <pre> | ||
>> D | >> D | ||
| Zeile 278: | Zeile 276: | ||
0 0 0 0 0 0 -0.0016 0 | 0 0 0 0 0 0 -0.0016 0 | ||
0 0 0 0 0 0 0 -0.0000 | 0 0 0 0 0 0 0 -0.0000 | ||
</ | </pre> | ||
Die zugehörigen dimensionslosen Periodendauern sind | Die zugehörigen dimensionslosen Periodendauern sind | ||
<math>\begin{array}{ll}T_1 = & 0.0037\\ T_2 = & 0.0061\\ T_3 = & 0.0096\\ T_4 = & 0.0154 \\ T_5 = & 0.0287 \\ T_6 = & 0.0566 \\ T_7 = & 0.1594 \\ T_8 = & 1.0000\end{array}</math>. | ::<math>\begin{array}{ll}T_1 = & 0.0037\\ T_2 = & 0.0061\\ T_3 = & 0.0096\\ T_4 = & 0.0154 \\ T_5 = & 0.0287 \\ T_6 = & 0.0566 \\ T_7 = & 0.1594 \\ T_8 = & 1.0000\end{array}</math>. | ||
Und offensichtlich fällt die längste Periodendauer ''T<sub>8</sub>'' mit der analytisch berechneten untersten Schwingunsperiode ''T<sup>*</sup>'' zusammen. | Und offensichtlich fällt die längste Periodendauer ''T<sub>8</sub>'' mit der analytisch berechneten untersten Schwingunsperiode ''T<sup>*</sup>'' zusammen. | ||
Die zugehörigen Eigenvektoren stehen in ''V'': | Die zugehörigen Eigenvektoren stehen in ''V'': | ||
< | <pre> | ||
>> V | >> V | ||
| Zeile 299: | Zeile 297: | ||
-0.9540 -0.8313 -0.8232 0.9212 -0.6357 0.7308 0.7663 -0.8013 | -0.9540 -0.8313 -0.8232 0.9212 -0.6357 0.7308 0.7663 -0.8013 | ||
-0.2099 -0.1390 -0.0999 0.0809 -0.0389 0.0315 0.0200 -0.0060 | -0.2099 -0.1390 -0.0999 0.0809 -0.0389 0.0315 0.0200 -0.0060 | ||
</ | </pre> | ||
Die Eigenvektoren in ''V'' spannen nun den Nullraum (nullspace) der Matrix auf, es ist | Die Eigenvektoren in ''V'' spannen nun den Nullraum (nullspace) der Matrix auf, es ist | ||
| Zeile 317: | Zeile 315: | ||
<tr><th>Mode</th><th>Modalform ''ϕ<sub>j</sub>(x)''</th><th>Mode</th><th>Modalform ''ϕ<sub>j</sub>(x)''</th></tr> | <tr><th>Mode</th><th>Modalform ''ϕ<sub>j</sub>(x)''</th><th>Mode</th><th>Modalform ''ϕ<sub>j</sub>(x)''</th></tr> | ||
<tr> | <tr> | ||
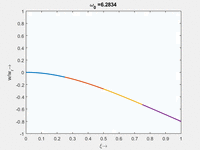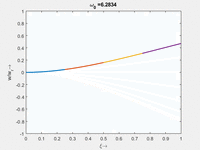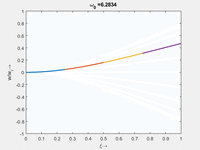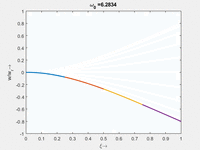
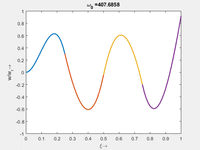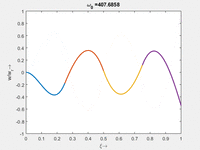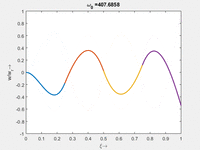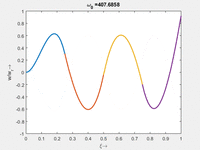
<td | <td>#8<br/<math>\displaystyle \omega_{0,8} = 1.000\cdot \frac{2 \pi}{T_{ref}}</math></td> | ||
<td | <td></td> | ||
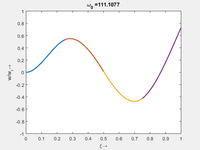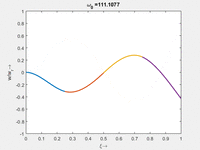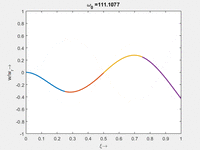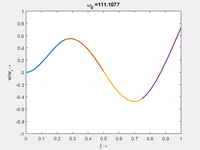
< | <td>#7<br/><math>\displaystyle \omega_{0,7} = 6.2742\cdot \frac{2 \pi}{T_{ref}}</math></td> | ||
<td | <td></td> | ||
</tr> | </tr> | ||
<td | <tr> | ||
<td | <td>#6<br/><math>\displaystyle \omega_{0,6} = 17.6833\cdot \frac{2 \pi}{T_{ref}}</math></td> | ||
< | <td></td> | ||
<td | <td>#5<br/><math>\displaystyle \omega_{0,5} = 34.8854\cdot \frac{2 \pi}{T_{ref}}</math></td> | ||
<td></td> | |||
</tr> | </tr> | ||
<tr> | |||
<td>#4<br/><math>\displaystyle \omega_{0,4} = 64.8852\cdot \frac{2 \pi}{T_{ref}}</math></td> | |||
<td></td> | |||
< | <td>#3<br/><math>\displaystyle \omega_{0,3} = 104.2059\cdot \frac{2 \pi}{T_{ref}}</math></td> | ||
<td></td> | |||
</tr> | |||
<math>\displaystyle \omega_{0, | |||
< | |||
< | |||
<math>\displaystyle \omega_{0,3} = 104.2059\cdot \frac{2 \pi}{T_{ref}}</math> | |||
{{MyTip|title=Zur Euler-Bernoulli-Hypothese|text= | {{MyTip|title=Zur Euler-Bernoulli-Hypothese|text= | ||
| Zeile 373: | Zeile 340: | ||
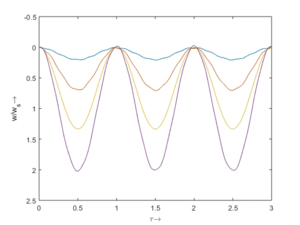
[[Datei:FEAG-modes-all.png|mini|Modalformen]]Alle acht Moden ''ϕ<sub>j</sub>'' können wir auch zum Zeitpunkt ''τ=0'' übereinander darstellen: | [[Datei:FEAG-modes-all.png|mini|Modalformen]]Alle acht Moden ''ϕ<sub>j</sub>'' können wir auch zum Zeitpunkt ''τ=0'' übereinander darstellen: | ||
}} | }} | ||
Version vom 25. Februar 2021, 08:59 Uhr
Aufgabenstellung
Analog zu FEAF untersuchen wir hier die Schwingungen eines Kontinuums beim Loslassen aus der entspannten Rugelage. Hier nicht mit einem Dehnstab, sondern einem Euler-Bernoulli-Balken.
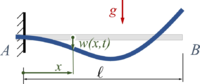
Gesucht ist die Schwingung eines Euler-Bernoulli-Balkens beim Loslassen aus der Ruhelage. Wir gehen nach dem Standardrezept der Finite Elemente Methode vor, arbeiten also mit dem Sources/Lexikon/Prinzip der virtuellen Arbeit.
Lösung mit Matlab
Interessant ist hier, dass - im Gegensatz zu Stablängsschwingungen - die Eigenfrequenz nicht ein gerades Vielfaches der untersten Eigenfrequenz ist. Falls Sie ein Saiteninstrument spielen, verstehen Sie sofort, warum das wichtig ist.
Maxima können wir hier nicht gut gebrauchen: die Gleichungen werden zu umfangreich. Wir arbeiten also mehr mit numerischen Verfahren, da ist Matlab geeigneter. Allerdings können wir Matlab-Inhalte nicht gut auf dieser Seite unterbringen - deshalb gibt es dafür die Seite FEAG-Matlab, die der gleichen Struktur folgt.
Header
Im Programm arbeiten wir mit einer dimensionslosen Formulierung - wir brauchen dafür eine Bezugszeit tBez und eine Bezugslänge lBez.
Bezugsgrößen wählen
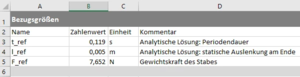
Dazu nehmen wir eine "Anleihe" bei der analytischen Lösung des Schwingungsproblems (vgl. Aufgabe SKEB):
|
Analytische Lösung: homohener Lösungsanteil |
Analytische Lösung: partikularer Lösungsanteil |
|---|---|
|
Die homogene Bewegungsgleichung des Euler-Bernoulli-Balkens hat Lösungen vom Typ Wir bekommen zu jedem ω0 vier κ Das α ist eine praktische Abkürzung, hinter der wir ω0 verstecken. Anders als beim Dehnstab (SKER) finden wir hier keine analytische Beziehung, sondern nur die numerischen Beziehungen, für die unsere Randbedingungen erfüllt sind: Die langsamste Eigenmode gehört zu α1 mit der Periodendauer
Also wählen wir . |
Die zugeordnete inhomogene Bewegungsgleichung des Euler-Bernoulli-Balkens hat die partikulare Lösung Die statische Auslenkung am unteren Ende ist demnach
Wir wählen \ell_{Bez} := w_s. |
System-Parameter des FEM-Modells
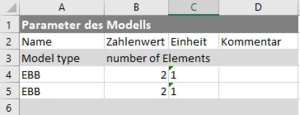
Für die Diskretisierung wählen wir als Anzahl der Finiten Elemente (Number Of Elements):
und damit je Element
.
Wir wählen die kubische Ansatzfunktionen aus dem Abschnitt Finite Elemente Methode je Element, also
Für die numerisch Implementierung stört in dieser Darstellung das Element-spezifische ℓi - die Elementlänge. Wir behelfen uns, indem wir die Ansatzfunktionen schreiben als
,
wobei wir die Ansatz-Polynome in verpacken.
Das schaut unnötig komplex aus - allerdings stecken wir die Diagonal-Matrizen d (für jedes Element eine) in eine Matlab-Variable, so dass sie dort nicht weiter auffällt.
Die abhängigen Koordinaten des FEM-Modells sind dann zunächst - bis zum Einarbeiten der Randbedingungen - diese:
.
Equilibrium Conditions
Die Gleichgewichtsbedingung mit dem Prinzip der virtuellen Verrückungen setzen sich additiv aus
- ,
zusammen - also den virtuellen Arbeiten je Element zuzüglich von virtuellen Arbeiten am Rand. In unserem Beispiel haben wir allerdings keine eingeprägten, äußeren Lasten am Rand, also ist
- .
Je Element erfassen wir die virtuellen Arbeiten durch Element-Matrizen. So ist z.B. für die virtuelle Formänderungsenergie (vgl. Finite Elemente Methode)
mit der Element-Steifigkeitsmatrix .
Aus der FEM-Formulierung für den Euler-Bernoulli-Balken könnten wir die Element-Matrizen der virtuellen Arbeit der D'Alembert'schen Trägheitskraft sowie der Virtuelle Formänderungsenergie herauskopieren. Auch die "rechte Seite" mit der virtuelle Arbeit der Gewichtskraft aus
- ,
könnten wir als Element-Lastmatrix (Spaltenmatrix) abspeichern.
- .
Dass es auch anders geht,sehen Sie in der Definition der Matlab-Klasse FEM_Element_Modell, bei der die Element direkt aus den Trial-Functions - hier den
- -
hergeleitet. werden:
:
K(row,col) = diff(...
polyval(...
polyint(...
conv(polyder(self.phi(row,:)),polyder(self.phi(col,:)))),...
[0,1]));
:
Komponieren der System-Matrizen
Die System-Matrizen des Gesamt–Systems komponieren wir nun durch Hinzuaddieren der Anteile je Element.
Beispiel: die Gesamt-Steifigkeitsmatrix für I=2:
Die Beiträge der zwei Elemente sind hier in rot bzw. grün eingefärbt.
Dieses "Hinzuaddieren" passiert in Matlab hier:
:
e = 0;% counter for all elements of all sections
for section = 1: length(element.noe)
:
for i = 1:element.noe(section)
e = e+1;
:
j = 2*(e-1)+1;
:
K(j:j+3,j:j+3) = K(j:j+3,j:j+3)+b* d(:,:,e)*element.K*d(:,:,e);
:
end
:
In Matrix-Schreibweise lautet die Bewegungsgleichung des Gesamt-Systems jetzt:
- .
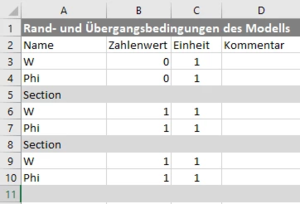
Einarbeiten der Randbedingungen
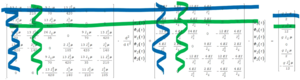
Die Randbedingungen arbeiten wir ein, indem wir zeilenweise (für δW und δΦ) und spaltenweise (für W und Φ) streichen.
Hier sind es
- die erste Zeile/Spalte für W0 (blau) und
- die zweite Zeile / Spalte für Φ0 (grün).
Solving
Die Lösung des Anfangs- und Randwertproblems ist in diesem Lösungsansatz mit Matlab um die Klasse "FEM_Container" herum aufgebaut - in ihr sind alle Parameter und Lösungsprozesse beschrieben.
Hier heißt die Instanz des Modells
- mathModel
In diesem Container sind alle Parameter und Zustandsgrößen des Modells bereits dimensionslos gemacht - und zwar mit den oben genannten Bezugsgrößen, die in der Excel-Eingabedatei im Blatt "0) Bezugsgrößen" definiert sind.
Die Lösung des Anfangswertproblems setzt sich aus zwei Teilen zusammen:
- der partikularen Lösung, die die Rechte Seite "G" erfüllt und
- der homogenen Lösung, die die Rechte Seite "0" erfüllt.
Die Gesamtlösung Qt setzt sich nun - bei diesem linearen System - additiv aus partikularer Qp und Qh homogener Lösung zusammen:
Particular Solution
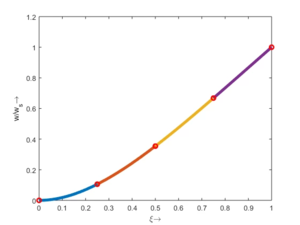
Die rechte Seite der Bewegungsgleichung G ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung Qp statisch, wir suchen nach der Lösung des Gleichungssystems
und die ist - mit der Normierung durch ws -
>> Qp
Qp =
0
0
0.1055
0.0042
0.3542
0.0064
0.6680
0.0072
1.0000
0.0073
Diese Lösung tragen wir - elementweise - auf.
Homogene Lösung
Zur Lösung der homogenen Bewegungsgleichung
setzen wir an
und erhalten das Eigenwertproblem
mit
| den Eigenwerten | und |
| den Egenvektoren | . |
Für die Berechnung der Eigenwerte λ müssen wir die Abkürzung
einführen. Damit arbeitet die Matlab-Routine "eig()", die in "mathModel.eigensystem()" implementiert ist.
Acht Eigenwerte kommen aus der Bedingung , diese werden auf der Spur der Matrix D abgelegt:
>> D
D =
1.0e+06 *
-2.9006 0 0 0 0 0 0 0
0 -1.0774 0 0 0 0 0 0
0 0 -0.4287 0 0 0 0 0
0 0 0 -0.1662 0 0 0 0
0 0 0 0 -0.0480 0 0 0
0 0 0 0 0 -0.0123 0 0
0 0 0 0 0 0 -0.0016 0
0 0 0 0 0 0 0 -0.0000
Die zugehörigen dimensionslosen Periodendauern sind
- .
Und offensichtlich fällt die längste Periodendauer T8 mit der analytisch berechneten untersten Schwingunsperiode T* zusammen.
Die zugehörigen Eigenvektoren stehen in V:
>> V
V =
-0.0579 0.2951 -0.0687 0.3043 0.4561 0.5309 -0.3197 -0.0780
-0.0129 0.0882 -0.0805 -0.0578 -0.0115 0.0064 -0.0096 -0.0032
-0.0884 -0.1020 0.4873 -0.0417 -0.4707 0.0160 -0.5469 -0.2721
-0.0364 0.1230 0.0134 0.0659 -0.0007 -0.0222 0.0019 -0.0051
-0.1652 -0.4100 -0.2420 -0.1979 0.4058 -0.4268 -0.1035 -0.5270
-0.0763 0.0330 0.0704 -0.0601 0.0098 0.0106 0.0163 -0.0059
-0.9540 -0.8313 -0.8232 0.9212 -0.6357 0.7308 0.7663 -0.8013
-0.2099 -0.1390 -0.0999 0.0809 -0.0389 0.0315 0.0200 -0.0060
Die Eigenvektoren in V spannen nun den Nullraum (nullspace) der Matrix auf, es ist
Die homogene Lösung der Bewegungsgleichung lautet damit
mit den acht Integrationskonstanten Ci . Durch die komplexen Eigenwerte sind die Integrationskonstanten nun (eigentlich) auch komplexwertig. Darum kommen in diesem Fall herum, weil die Anfangsgeschwindigkeit des Balkens beim Loslassen Null ist - wir also nur cos-Anteile berücksichtigen müssen. Und die gehören wiederum zum Realteil der Exponential-Funktion.
Die Ci sind nun die Konstanten, die wir brauchen, um die Lösung an Anfangsbedingungen anzupassen.
Vorher schauen wir uns die Lösung jeweils zu einer Eigenfrequenz ωi an. Diese Funktionen heißen Modalformen ϕ(x) und deren Schwingungen können wir plotten:
| Mode | Modalform ϕj(x) | Mode | Modalform ϕj(x) |
|---|---|---|---|
| #8<br/ | #7 |
||
| #6 |
#5 |
||
| #4 |
#3 |
| ✔ Zur Euler-Bernoulli-Hypothese: |
| Praktisch haben die höheren Moden kaum Relevanz - meist klingen sie durch Dämpfung schnell ab. Man sieht allerdings bereits an der Schwingungs-Form, dass hier die Länge zwischen zwei Knoten nicht mehr sehr klein ist im Vergleich zur Höhe. Und das führt dazu, dass Schubverformungen eine Rolle spielen. Wir müssen zum Timoshenko-Balken wechseln .... |
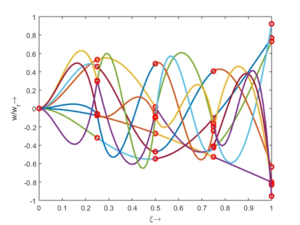
Alle acht Moden ϕj können wir auch zum Zeitpunkt τ=0 übereinander darstellen:
Adapt to Initial Conditions
xffsd
Post-Processing
xffsd
Header
xffsd
Header
xffsd
Links
- ...
Literature
- ...
 |
 |
 |
| ||
| ||
|