Gelöste Aufgaben/FEAG: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 13: | Zeile 13: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Analog zu [[FEAF]] untersuchen wir hier die Schwingungen eines Kontinuums beim Loslassen aus der entspannten Rugelage. Hier nicht mit einem [[Dehnstab]], sondern einem [[Euler-Bernoulli-Balken]]. | Analog zu [[Gelöste Aufgaben/FEAF|FEAF]] untersuchen wir hier die Schwingungen eines Kontinuums beim Loslassen aus der entspannten Rugelage. Hier nicht mit einem [[Sources/Lexikon/Dehnstab|Dehnstab]], sondern einem [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]]. | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:FEAG-01.png|mini|Lageplan|alternativtext=|200x200px]] | ||
Gesucht ist | Gesucht ist die Schwingung eines [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]]<nowiki/>s beim Loslassen aus der Ruhelage. Wir gehen nach dem Standardrezept der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finite Elemente Methode]] vor, arbeiten also mit dem [[Sources/Lexikon/Prinzip der virtuellen Arbeit]]. | ||
</onlyinclude> | </onlyinclude> | ||
== Lösung mit | == Lösung mit Matlab == | ||
Interessant ist hier, dass - im Gegensatz zu Stablängsschwingungen - die Eigenfrequenz nicht ein gerades Vielfaches der untersten Eigenfrequenz ist. Falls Sie ein Saiteninstrument spielen, verstehen Sie sofort, warum das wichtig ist. | |||
<!--------------------------------------------------------------------------------> | [[Maxima]] können wir hier nicht gut gebrauchen - wir arbeiten mehr mit numerischen Verfahren, da ist [[Matlab]] geeigneter. | ||
{{ | Allerdings können wir Matlab-Inhalte nicht gut auf dieser Seite unterbringen - deshalb gibt es dafür die Seite [[FEAG-Matlab]]. | ||
<!-------------------------------------------------------------------------------->{{MyNoncodeBlock|title=Header | |||
|text=Text | |text=Text | ||
}} | }} | ||
| Zeile 39: | Zeile 38: | ||
Version vom 25. Februar 2021, 06:43 Uhr
Aufgabenstellung
Analog zu FEAF untersuchen wir hier die Schwingungen eines Kontinuums beim Loslassen aus der entspannten Rugelage. Hier nicht mit einem Dehnstab, sondern einem Euler-Bernoulli-Balken.
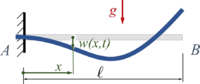
Gesucht ist die Schwingung eines Euler-Bernoulli-Balkens beim Loslassen aus der Ruhelage. Wir gehen nach dem Standardrezept der Finite Elemente Methode vor, arbeiten also mit dem Sources/Lexikon/Prinzip der virtuellen Arbeit.
Lösung mit Matlab
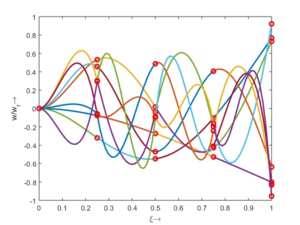
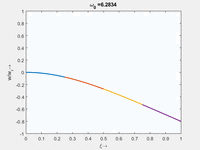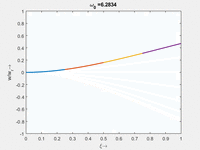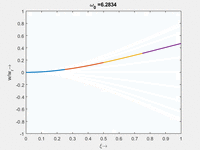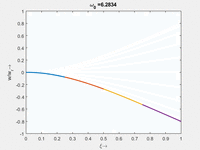
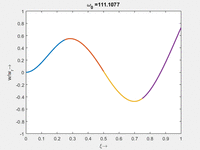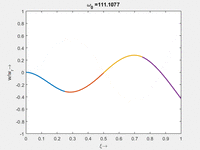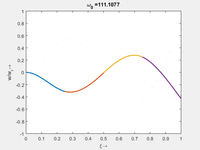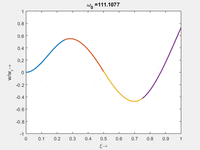
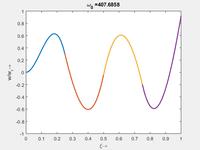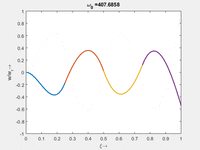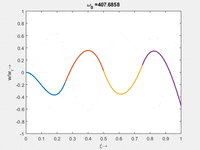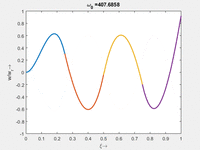
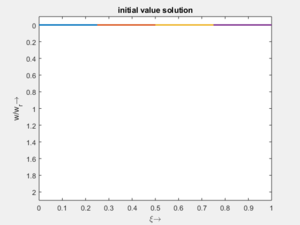
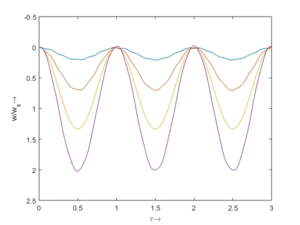
Interessant ist hier, dass - im Gegensatz zu Stablängsschwingungen - die Eigenfrequenz nicht ein gerades Vielfaches der untersten Eigenfrequenz ist. Falls Sie ein Saiteninstrument spielen, verstehen Sie sofort, warum das wichtig ist.
Maxima können wir hier nicht gut gebrauchen - wir arbeiten mehr mit numerischen Verfahren, da ist Matlab geeigneter. Allerdings können wir Matlab-Inhalte nicht gut auf dieser Seite unterbringen - deshalb gibt es dafür die Seite FEAG-Matlab.
Header
Text
Links
- ...
Literature
- ...
 |
 |
 |
| ||
| ||
|