Gelöste Aufgaben/COVI: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 35: | Zeile 35: | ||
<br /> | <br /> | ||
{{MyCodeBlock|title=Header|text=Wir lösen hier das Anfangswertproblem zu nichtlinearen Bewegungsgleichungen. | |||
Diese Gleichungen haben wir nicht - wir entwickeln sie ad-hoc und achten nur darauf, zentrale Phänomene abzubilden. Eine Abbildung der realen Zahlen ist nicht beabsichtigt.|code=1+1+=2}} | |||
| Zeile 46: | Zeile 45: | ||
! colspan="2" style="text-align:left;" |Header | ! colspan="2" style="text-align:left;" |Header | ||
|- | |- | ||
| style="width: 50%; vertical-align:top;" | | | style="width: 50%; vertical-align:top;" | | ||
|<syntaxhighlight lang="notmuch"> | |<syntaxhighlight lang="notmuch"> | ||
/*******************************************************/ | /*******************************************************/ | ||
Version vom 16. Februar 2021, 08:35 Uhr
Aufgabenstellung
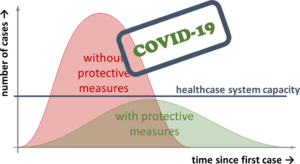
Als Ingenieure können wir die COVID-19-Epidemie genauso modellieren, wie technische Systeme.
Wir brauchen dazu "Koordinaten" - also Messgrößen - die die Anzahl der Individuen erfassen, die
- ansteckbar "a",
- infiziert "i" - mit und ohne Sympthome - und
- genesen "r"
sind. Für jede dieser Koordinaten müssen wir nun "Bewegungsgleichungen" - also z.B. Differentialbeziehungen in der Zeit - hinschreiben.
Das nennen wir "Modellbildung".
| 🧨 Dies ist kein zuverlässiges Prognosewerkzweug: |
Hier geht es um die Modellierung
|
Diese algebraischen und Differentialgleichungen sind dabei nicht das Ergebnis von Gleichgewichtsbeziehungen wie in der Technischen Mechanik. Wir begnügen uns statt dessen damit, Phänomene der Epidemie mit unserer Mathematik zu erfassen.
Und so gehen wir vor:
Wir modellieren eine Grundgesamtheit von n0 = 80 Millionen Individuen.
Die Pandemie soll bei einer Durchseuchung von α=50% zum Stillstand kommen - die Individuen sind dann so weit voneinander entfernt, dass eine Ansteckung unwahrscheinlich ist.
Zum Zeitpunkt t0=0 seien von insgesamt i0 Individuen mit
infiziert.
Header
Wir lösen hier das Anfangswertproblem zu nichtlinearen Bewegungsgleichungen. Diese Gleichungen haben wir nicht - wir entwickeln sie ad-hoc und achten nur darauf, zentrale Phänomene abzubilden. Eine Abbildung der realen Zahlen ist nicht beabsichtigt.
1+1+=2
Lösung mit Maxima
| Header | |
|---|---|
/*******************************************************/
/* declare variational variables */
declare("δW", alphabetic); /* virtual work */
declare("δA", alphabetic); /* virtual work of implied external forces */
declare("δΠ", alphabetic); /* virtual strain energy */
declare("δu", alphabetic); /* variation of u */
declare("δw", alphabetic);
declare("δφ", alphabetic);
declare("δη", alphabetic);
declare("δθ", alphabetic);
declare("λ" , alphabetic); /* otherwise, this is the lambda fct. */
declare("μ" , alphabetic);
declare("Δr", alphabetic); /*displacement of material point [x,y,z] */
declare("δΔr",alphabetic); /* variation of Δr */
declare("δZ", alphabetic); /* variation of strain */
/*******************************************************/
/* parameters */
/* abbreviate: */
geometry : [h^3 = 12*I[y]/b, b^3 = 12*I[z]/h, b = A/h];
/* Lame's Constants */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
lameConst : [λ = e*nu/((1+nu)*(1-2*nu)), μ = e/(2*(1+nu))];
/* relation: hook's law, modulus of elasticity */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
E : matrix([2*μ+λ, λ, λ, 0, 0, 0],
[ λ, 2*μ+λ, λ, 0, 0, 0],
[ λ, λ, 2*μ+λ, 0, 0, 0],
[ 0, 0, 0, μ, 0, 0],
[ 0, 0, 0, 0, μ, 0],
[ 0, 0, 0, 0, 0, μ]);
/* Strain Displacement Relation */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
StrainDispl(arg) := [epsilon[x,x] = diff(arg[1],x),
epsilon[y,y] = diff(arg[2],y),
epsilon[z,z] = diff(arg[3],z),
epsilon[x,y] = 1/2*(diff(arg[1],y) + diff(arg[2],x)),
epsilon[x,z] = 1/2*(diff(arg[1],z) + diff(arg[3],x)),
epsilon[y,z] = 1/2*(diff(arg[2],z) + diff(arg[3],y))];
| |