Gelöste Aufgaben/FEAE: Unterschied zwischen den Versionen
| Zeile 9: | Zeile 9: | ||
| Zeile 16: | Zeile 15: | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei:FEAE-01.png|mini|80px|Lageplan]] | [[Datei:FEAE-01.png|mini|80px|Lageplan]] | ||
Gesucht ist Gesamtlösung des Systems im Zeitbereich beim Loslassen der beiden Massen aus der Referenz-Konfiguration, bei der beide Federn entspannt sind. | Gesucht ist Gesamtlösung des Systems im Zeitbereich beim Loslassen der beiden Massen aus der Referenz-Konfiguration, bei der beide Federn entspannt sind. Wir stellen die Bewegungsgleichung mit dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip der virtuellen Verrückungen|Prinzip der virtuellen Verrückungen]] auf. | ||
</onlyinclude> | </onlyinclude> | ||
Wir arbeiten mit den System-Parametern | |||
== | <math>\begin{array}{ccc}k_1&=&\frac{3}{2} k_0\\k_2&=&k_0\\m_1&=&m_0\\m_2&=&m_0\\\end{array}</math> | ||
== Lösung mit Maxima == | |||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Header | <!-------------------------------------------------------------------------------->Der Lösungsweg zu dieser Aufgabe wird bereits in [[Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen/Integration der Differentialbeziehung (IVP)|Integration der Differentialbeziehung (IVP)]] gezeigt, hier verfolgende wir einen etwas allgemeineren Lösungspfad. | ||
Dabei arbeiten wir u.a. mit quadratischen Gleichungen. Für deren Lösung müssen wir [[Sources/Lexikon/Maxima|Maxima]] wissen lassen, welche Parameter positiv sind, also | |||
<math>k_0 > 0,\;\;\;m_0>0,\;\;\;T>0;</math>[[Datei:FEAW-02.png|mini|Koordinaten der Bewegung.|alternativtext=|185x185px]]Die Lage-Koordinaten des Systems fassen wir in | |||
<math>\underline{Q} = \left(\begin{array}{l}w_1(t)\\w_2(t)\end{array}\right)</math> | |||
zusammen. | |||
Für die [[Werkzeuge/Beschreibung physikalischer Systeme/Dimensionen und Einheiten|dimensionslose Schreibweise]] brauchen wir später eine Bezugszeit ''t<sub>Bez</sub>''. | |||
Dazu nehmen wir eine "Anleihe" bei einem ähnlichen System: | |||
Für dieses System "kennen" wir die Eigenkreisfrequenz | |||
<math>\displaystyle \omega_0 = \sqrt{\displaystyle\frac{k_0}{m_0}} \text{ und } \omega = \frac{2\pi}{T}</math>. | |||
Aus diesem Modell "leihen" wir uns die Bezugszeit zu | |||
<math>\displaystyle T = 2\pi \sqrt{\displaystyle\frac{m_0}{k_0}}</math>. | |||
und wählen | |||
<math>t_{Bez} := T</math>[[Datei:FEAE-03.png|mini|Hier kennen wir ω<sub>0</sub>.|alternativtext=|links|90x90px]]{{MyCodeBlock|title=Header | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 34: | Zeile 58: | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Equilibrium Conditions | <!-------------------------------------------------------------------------------->Die Gleichgewichtsbedingung mit dem Prinzip der virtuellen Verrückungen lautet | ||
<math>\begin{array}{lcl}\delta W &=& \underbrace{-m_1\cdot\ddot{w}_1\cdot\delta{w}_1-m_2\cdot\ddot{w}_2\cdot\delta{w}_2 + m_1\cdot g \cdot \delta w_1 + m_2\cdot g \cdot \delta w_2}_{\displaystyle := \delta W^a}\\&& - \underbrace{k_1\cdot{w}_1\cdot\delta{w}_1+k_2\cdot\left({w}_2-{w}_1\right)\cdot\left(\delta{w}_2-\delta{w}_1\right)}_{\displaystyle := \delta \Pi}\\&\stackrel{!}{=}0\end{array}</math>. | |||
Aufgelöst nach den Koeffizienten der virtuellen Verrückungen folgt die gewöhnliche, lineare Differentialgleichung: | |||
<math>\left(\begin{array}{cc} m_0&0\\0&m_0\end{array}\right)\cdot\left(\begin{array}{c}\ddot{w}_1\\ \ddot{w}_2\end{array}\right) + \left(\begin{array}{cc} \frac{5}{2}k_0&-k_0\\-k_0&k_0\end{array}\right)\cdot\left(\begin{array}{c}w_1\\ w_2\end{array}\right) = \left(\begin{array}{c}m_0\cdot g\\m_0\cdot g\end{array}\right)</math>. | |||
In dieser Beziehung stehen jetzt nur noch ''m<sub>0</sub>'' und ''k<sub>0</sub>'' - die Indizes "0" können wir also ab hier weglassen. In Matrix-Schreibweise lautet die Bewegungsgleichung jetzt: | |||
<math>\underline{\underline{M}}\cdot\underline{\ddot{Q}} + \underline{\underline{K}}\cdot\underline{Q} = \underline{G}</math>. | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 43: | Zeile 79: | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Solving | <!-------------------------------------------------------------------------------->Die Lösung des Anfangswertproblems setzt sich aus zwei Teilen zusammen: | ||
* der partikularen Lösung, die die Rechte Seite "''G''" erfüllt und | |||
* der homogenen Lösung, die die Rechte Seite "''0''" erfüllt. | |||
Die Gesamtlösung ''Q<sub>t</sub>'' setzt sich nun - bei diesem linearen System - additiv aus partikularer ''Q<sub>p</sub>'' und ''Q<sub>h</sub>'' homogener Lösung zusammen: | |||
<math>\underline{Q}_t(t) = \underline{Q}_p(t) + \underline{Q}_h(t)</math>{{MyCodeBlock|title=Solving | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 52: | Zeile 95: | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Right-Hand-Side Approach | <!-------------------------------------------------------------------------------->Die rechte Seite der Bewegungsgleichung ''G'' ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung ''Q<sub>p</sub>'' - die partikulare Lösung - statisch, wir suchen nach der Lösung des Gleichungssystems | ||
<math>\underline{\underline{K}}\cdot\underline{Q}_p = \underline{G}</math> | |||
und die ist | |||
<math>\underline{Q}_p = \begin{pmatrix}\displaystyle \frac{4\;{{m}}\;g}{3\;{{k}}}\\\displaystyle \frac{7\;{{m}}\;g}{3\;{{k}}}\end{pmatrix}</math> | |||
Wir führen die Abkürzung | |||
<math>\displaystyle w_s = \frac{{{m}}g}{{{k}}}</math> | |||
ein, also ist | |||
<math>\underline{Q}_p = w_s\cdot\begin{pmatrix}\displaystyle \frac{4}{3}\\\displaystyle \frac{7}{3}\end{pmatrix}</math>.{{MyCodeBlock|title=Right-Hand-Side Approach | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 60: | Zeile 117: | ||
}} | }} | ||
==tmp== | ==tmp== | ||
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Homogeneous Solution | <!-------------------------------------------------------------------------------->Für die Lösung der homogenen Bewegungsgleichung | ||
<math>\underline{\underline{M}}\cdot\underline{\ddot{Q}} + \underline{\underline{K}}\cdot\underline{Q} = \underline{0}</math> | |||
setzen wir (vgl. [[Sources/Lexikon/Modalanalyse|Modalanalyse]]) an | |||
<math>\displaystyle \underline{Q}_h = \underline{\hat{Q}}_h\cdot e^{\lambda\cdot t}</math> | |||
und erhalten das [[Werkzeuge/Lösungsbausteine der Mathematik/Eigenwertprobleme|Eigenwertproblem]] | |||
<math>\underbrace{\left(\lambda^2 \underline{\underline{M}} + \underline{\underline{K}}\right)}_{\displaystyle \underline{\underline{D}}(\lambda)}\cdot\underline{\hat{Q}}_h = \underline{0}</math> | |||
mit | |||
{| class="wikitable" | |||
|den Eigenwerten | |||
|<math>\lambda</math> | |||
|und | |||
|- | |||
|den Eigenvektoren | |||
|<math>\displaystyle \underline{\hat{Q}}_{h}</math> | |||
|. | |||
|} | |||
Die Berechnung der Eigenwerte ''λ'' wird einfacher mit | |||
<math>\lambda^2 = -\Lambda</math> | |||
und wir transformieren parallel die Bewegungsgleichungen auf die dimensionslose Zeit | |||
<math>\displaystyle \tau := \frac{t}{t_{Bez}}</math> mit <math>t_{Bez} = T.</math>, | |||
also | |||
<math>\displaystyle \underline{\ddot{Q}} = \frac{d^2\underline{Q}}{d\tau^2}\cdot\underbrace{\frac{d^2\tau}{dt^2}}_{\displaystyle \frac{1}{T^2}}</math>. | |||
Wir finden zwei Eigenwerte aus der Bedingung det(''D'')=0: | |||
<math>\begin{array}{lr}\Lambda_1 = &2 \cdot \pi^2\\\Lambda_2 = &12 \cdot \pi^2\\\end{array}</math> | |||
und | |||
<math>\begin{array}{lr}\lambda_1 = &j \cdot \sqrt{2} \cdot \pi\\\lambda_2 = &j \cdot 2\sqrt(3) \cdot \pi\\\end{array} \text{ mit } j := \sqrt{-1}</math>. | |||
Für die Matrix | |||
<math>\displaystyle \underline{\underline{D}}(\lambda_i) = \lambda^2\cdot \frac{1}{T^2}\cdot \underline{\underline{M}} + \underline{\underline{K}}</math> | |||
stellen wir fest: | |||
Die Matrix hat | |||
* einen Rang (rank) von 1 - es gibt eine linear abhängige Zeile im Gleichungssystem und - entsprechend - | |||
* einen Rangabfall (nullity) von 1. | |||
Die Eigenvektoren spannen nun den Nullraum (nullspace) der Matrix auf. Normmert auf die Länge 1 sind das | |||
* für ''λ<sub>1</sub>'': | |||
<math>\displaystyle \underline{\hat{Q}}_{h,1} = \frac{1}{\sqrt{5}} \cdot \left(\begin{array}{c}1\\2 \end{array}\right)</math> und | |||
* für ''λ<sub>2</sub>'': | |||
<math>\displaystyle \underline{\hat{Q}}_{h,2} = \frac{1}{\sqrt{5}} \cdot \left(\begin{array}{c}2\\-1 \end{array}\right)</math>. | |||
Die homogene Lösung der Bewegungsgleichung lautet damit | |||
<math>\displaystyle \underline{{Q}}_{h}(t) = c_1\cdot \frac{1}{\sqrt{5}} \cdot \left(\begin{array}{r}1\\2\end{array}\right) \cdot e^{\displaystyle j\cdot\sqrt{2}\pi \cdot \tau} + c_2\cdot \frac{1}{\sqrt{5}} \cdot \left(\begin{array}{r}2\\-1 \end{array}\right) \cdot e^{\displaystyle j\cdot 2\sqrt{3}\pi \cdot \tau}</math> | |||
mit den Integrationskonstanten ''c<sub>1</sub>'' und ''c<sub>2</sub>''. Durch die komplexen Eigenwerte sind die beiden Integrationskonstanten nun auch komplexwertig, also | |||
<math>\begin{array}{l}c_1 = c_{R,1} + j\cdot c_{I,1}\\c_2 = c_{R,2} + j\cdot c_{I,2}\end{array}</math>. | |||
Diese vier reell-wertigen Integrationskonstanten bekommen wir aus vier Anfangsbedingungen für die beiden Massen, hier | |||
<math>\begin{array}{l}w_1(0) = 0\\w_2(0) = 0\\\dot{w}_1(0) = 0\\\dot{w}_2(0) = 0\end{array}</math>. | |||
Wir finden | |||
<math>\displaystyle {{c}_{R,1}}=-\frac{6\;{{m}}\;g}{\sqrt{5}\;{{k}}},{{c}_{I,1}}=0,{{c}_{R,2}}=-\frac{{{m}}\;g}{3\;\sqrt{5}\;{{k}}},{{c}_{I,2}}=0</math>. | |||
und damit | |||
<math>\underline{Q}_{h}(t) = 15\cdot \begin{pmatrix}-2\cos{\left( 2\sqrt{3}{\pi} \cdot \tau\right) }-18\cos{\left( \sqrt{2}{\pi} \cdot \tau\right) }\\ \cos{\left( 2\sqrt{3}{\pi} \cdot \tau\right) }-36\cos{\left( \sqrt{2}{\pi} \cdot \tau\right) }\end{pmatrix}</math>.{{MyCodeBlock|title=Homogeneous Solution | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 69: | Zeile 204: | ||
==tmp== | ==tmp== | ||
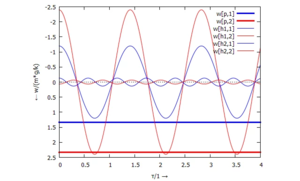
<!-------------------------------------------------------------------------------->{{MyCodeBlock|title=Post-Processing | <!-------------------------------------------------------------------------------->Die Lösung für | ||
* ''w<sub>1</sub>'' (blau) und | |||
* ''w<sub>2</sub>'' (rot) | |||
im Zeitbereich, angepasst an die Anfangsbedingungen, sieht nun so aus:[[Datei:FEAE-11.png|mini|Ergebnis-Plots für ''w<sub>1</sub>(t), w<sub>2</sub>(t).''|alternativtext=|ohne]]Interessant ist die separate Auftragung der Lösungsanteile nach partikularer Lösung (Index ''"p"'') und den beiden homogenen Lösungsanteilen (Index ''"h1", "h2"''). Man erkennt, wie die Summe jeweils der blauen und der roten Anteile die Gesamtlösung ergibt.[[Datei:FEAW-12.png|mini|Ergebnis-Plot mit den Lösungsanteilen.|alternativtext=|ohne]]{{MyCodeBlock|title=Post-Processing | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 79: | Zeile 219: | ||
Version vom 24. Februar 2021, 11:32 Uhr
Aufgabenstellung
Wir schauen uns die Lösungsanteile für die Bewegungsgleichung des Zwei-Masse-Schwinger an: welche Rolle spielen die homogene und partikulare Lösung?
Gesucht ist Gesamtlösung des Systems im Zeitbereich beim Loslassen der beiden Massen aus der Referenz-Konfiguration, bei der beide Federn entspannt sind. Wir stellen die Bewegungsgleichung mit dem Prinzip der virtuellen Verrückungen auf.
Wir arbeiten mit den System-Parametern
Lösung mit Maxima
tmp
Der Lösungsweg zu dieser Aufgabe wird bereits in Integration der Differentialbeziehung (IVP) gezeigt, hier verfolgende wir einen etwas allgemeineren Lösungspfad.
Dabei arbeiten wir u.a. mit quadratischen Gleichungen. Für deren Lösung müssen wir Maxima wissen lassen, welche Parameter positiv sind, also
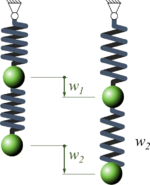
Die Lage-Koordinaten des Systems fassen wir in
zusammen.
Für die dimensionslose Schreibweise brauchen wir später eine Bezugszeit tBez.
Dazu nehmen wir eine "Anleihe" bei einem ähnlichen System:
Für dieses System "kennen" wir die Eigenkreisfrequenz
.
Aus diesem Modell "leihen" wir uns die Bezugszeit zu
.
und wählen
===Header===
Text
1+1
tmp
Die Gleichgewichtsbedingung mit dem Prinzip der virtuellen Verrückungen lautet
.
Aufgelöst nach den Koeffizienten der virtuellen Verrückungen folgt die gewöhnliche, lineare Differentialgleichung:
.
In dieser Beziehung stehen jetzt nur noch m0 und k0 - die Indizes "0" können wir also ab hier weglassen. In Matrix-Schreibweise lautet die Bewegungsgleichung jetzt:
.
Equilibrium Conditions
Text
1+1
tmp
Die Lösung des Anfangswertproblems setzt sich aus zwei Teilen zusammen:
- der partikularen Lösung, die die Rechte Seite "G" erfüllt und
- der homogenen Lösung, die die Rechte Seite "0" erfüllt.
Die Gesamtlösung Qt setzt sich nun - bei diesem linearen System - additiv aus partikularer Qp und Qh homogener Lösung zusammen:
===Solving=== Text
1+1
tmp
Die rechte Seite der Bewegungsgleichung G ist nicht zeitabhängig - sie ist statisch. Also ist auch die Lösung Qp - die partikulare Lösung - statisch, wir suchen nach der Lösung des Gleichungssystems
und die ist
Wir führen die Abkürzung
ein, also ist
.===Right-Hand-Side Approach=== Text
1+1
tmp
Für die Lösung der homogenen Bewegungsgleichung
setzen wir (vgl. Modalanalyse) an
und erhalten das Eigenwertproblem
mit
| den Eigenwerten | und | |
| den Eigenvektoren | . |
Die Berechnung der Eigenwerte λ wird einfacher mit
und wir transformieren parallel die Bewegungsgleichungen auf die dimensionslose Zeit
mit ,
also
.
Wir finden zwei Eigenwerte aus der Bedingung det(D)=0:
und
.
Für die Matrix
stellen wir fest:
Die Matrix hat
- einen Rang (rank) von 1 - es gibt eine linear abhängige Zeile im Gleichungssystem und - entsprechend -
- einen Rangabfall (nullity) von 1.
Die Eigenvektoren spannen nun den Nullraum (nullspace) der Matrix auf. Normmert auf die Länge 1 sind das
- für λ1:
und
- für λ2:
.
Die homogene Lösung der Bewegungsgleichung lautet damit
mit den Integrationskonstanten c1 und c2. Durch die komplexen Eigenwerte sind die beiden Integrationskonstanten nun auch komplexwertig, also
.
Diese vier reell-wertigen Integrationskonstanten bekommen wir aus vier Anfangsbedingungen für die beiden Massen, hier
.
Wir finden
.
und damit
.===Homogeneous Solution=== Text
1+1
tmp
Die Lösung für
- w1 (blau) und
- w2 (rot)
im Zeitbereich, angepasst an die Anfangsbedingungen, sieht nun so aus:
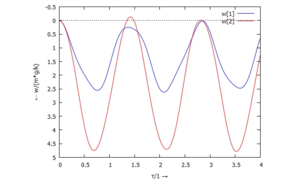
Interessant ist die separate Auftragung der Lösungsanteile nach partikularer Lösung (Index "p") und den beiden homogenen Lösungsanteilen (Index "h1", "h2"). Man erkennt, wie die Summe jeweils der blauen und der roten Anteile die Gesamtlösung ergibt.
===Post-Processing===
Text
1+1
Links
- ...
Literature
- ...