Gelöste Aufgaben/FEAD

Aufgabenstellung

Statt Formfunktionen über die ganze Stablänge anzusetzten wie in FEAB gehen wir jetzt nach der Methode der Finiten Elemente vor.

Caption

Lageplan

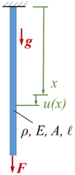
Gesucht ist die Näherungslösung für die statische Auslenkung der Stab-Querschnitte mit dem Prinzip der Virtuellen Verrückungen und dem Ansatz nach der Methode der Finiten Elemente. Dazu wir unterteilen die Struktur in Elemente und setzen Lineare Trialfunctions für die Verformung in den Elemeten an.

Lösung mit Matlab

Lorem Ipsum ....

tmp

Die Lösung basiert auf Maxima 16.04.2 - wir interessieren uns also vor allem für die Struktur der Lösung.===Header=== Text

1+1

tmp

Für Maxima brauchen wir einige Deklarationen.

Die Anzahl der Finiten-Elementen I wählen wir zu

$I=3$

Wir wählen Elemente gleicher Länge, also ist die Elementlänge l_i im Element i

${\begin{array}{ll}\ell _{i}&=\ell _{e}\\&=\ell _{0}/I\end{array}}$.===Declarations=== Text

1+1

tmp

Wir können die Trial-Functions als

$\displaystyle u(x)=\sum _{i=0}^{I}U_{i}\cdot \phi _{i}(x)$

mit

$\displaystyle \phi _{i}(x)=\left\{{\begin{array}{cl}\xi _{i-1}&{\text{ wobei }}x=\ell _{e}\cdot \left((i-1)+\xi _{i-1}\right),\;0<\xi _{i-1}<1\\\left(1-\xi _{i}\right)&{\text{ wobei }}x=\ell _{e}\cdot \left(i+\xi _{i}\right),\;0<\xi _{i}<1\end{array}}\right.$.

Für i=2 sieht die Trial-Function dann so aus:

Trial-Function für i=2.

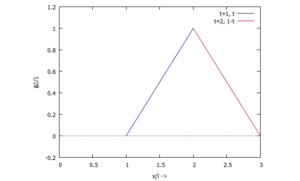
plot2d([[parametric, 1+t, t, [t,0,1]],[parametric, 2+t, 1-t, [t,0,1]]],

             [x,0,3], [y,-0.2,1.2],

             [xlabel, "x/l ->"], [ylabel, "ϕ2/1"])

Für die Methode der Finiten Elemente ist allerdings die Sichtweise je Elemement anschaulicher, also

$\displaystyle u_{i}(x_{i})=\left\{{\begin{array}{c}\displaystyle U_{i-1}\cdot \left(1-\left({\frac {x_{i}}{\ell _{i}}}\right)\right)+U_{i}\cdot \left({\frac {x_{i}}{\ell _{i}}}\right)\\0{\text{ sonst }}\end{array}}\right.$,

Und für Element i=2 wird der Verlauf der Querschnitts-Verschiebung also durch

$\displaystyle u_{2}(x_{2})=\left\{{\begin{array}{c}\displaystyle U_{1}\cdot \left(1-\left({\frac {x_{2}}{\ell _{2}}}\right)\right)+U_{2}\cdot \left({\frac {x_{2}}{\ell _{2}}}\right)\\0{\text{ sonst }}\end{array}}\right.$.

entsprechend

$\displaystyle \delta u_{2}(x_{2})=\left\{{\begin{array}{c}\displaystyle \delta U_{1}\cdot \left(1-\left({\frac {x_{2}}{\ell _{2}}}\right)\right)+\delta U_{2}\cdot \left({\frac {x_{2}}{\ell _{2}}}\right)\\0{\text{ sonst }}\end{array}}\right.$

beschreiben.

Bei 3 Finiten Elementen sind die System-Koordinaten dann

${\underline {Q}}=\left({\begin{array}{l}U_{0}\\U_{1}\\U_{2}\\U_{3}\end{array}}\right)$===Formfunctions=== Text

1+1

tmp

Die gesamte virtuelle Arbeit am System können wir nun als Summe der virtuellen Einzelarbeiten je Element hinschreiben, also

${\begin{array}{ll}\delta W&=\delta W^{a}-\delta \Pi \\&=\sum _{i=1}^{I}\left(\delta W_{i}^{a}-\delta \Pi _{i}\right)\end{array}}$.

Für jedes Element erhalten wir die virtuelle Formänderungsenergie

${\begin{array}{ll}\displaystyle \delta \Pi _{i}&=\int _{0}^{\ell _{i}}EA\cdot u_{i}'\cdot \delta u_{i}'\;dx_{i}\\\displaystyle &=\left(\delta U_{i-1},\delta U_{i}\right)\cdot \displaystyle {\frac {EA}{\ell _{i}}}\cdot \left({\begin{array}{rr}1&-1\\-1&1\end{array}}\right)\cdot \left({\begin{array}{l}U_{i-1}\\U_{i}\end{array}}\right)\end{array}}$

und die virtuelle Arbeit der äußeren, eingeprägten Gewichtskraft

${\begin{array}{ll}\displaystyle \delta W_{i}^{a}&=\int _{0}^{\ell _{i}}\varrho \cdot A\cdot g\cdot \delta u_{i}\;dx_{i}\\\displaystyle &={\frac {1}{2}}\cdot \left(\delta U_{i-1},\delta U_{i}\right)\cdot \varrho \cdot A\cdot g\cdot \ell _{i}\cdot \left({\begin{array}{l}1\\1\end{array}}\right)\end{array}}$.

Element-wise contributions to δW

Text

1+1

tmp

Für jedes Element müssen wir nun die virtuellen Arbeiten zum Gesamt-Gleichungssystem zusammenaddieren.

Die Gleichgewichtsbedingung

${\begin{array}{ll}\delta W&=\delta W^{a}-\delta \Pi \\&{\stackrel {!}{=}}0\end{array}}$

liefern ein Gleichungssystem, in das wir nun die kinematische Randbedingung U₀=0, δU₀=0 durch Streichen der ersten Zeile des Gleichungssystems und der ersten Spalte der Gesamt-Steifigkeitsmatrix einarbeiten.

Wir wählen nun noch für jedes Element die gleiche Element-Länge ℓ_i = ℓ_e, mit ℓ_e = ℓ₀/3 und es bleibt

$\displaystyle {\frac {EA}{\ell _{i}}}{\begin{pmatrix}2&-1&0\\-1&2&-1\\0&-1&1\end{pmatrix}}\cdot \left({\begin{array}{l}U_{1}\\U_{2}\\U_{3}\end{array}}\right)=\varrho A\ell _{i}g\cdot \left({\begin{array}{l}1\\1\\{\frac {1}{2}}\end{array}}\right)$.===Equlilibrium Conditions=== Text

1+1

tmp

Die Gleichgewichtsbedingungen lösen wir nun und erhalten

$\displaystyle {{U}_{0}}=0,{{U}_{1}}={\frac {5g\,{{\ell }_{i}^{2}}\varrho }{2E}},{{U}_{2}}={\frac {4g\,{{\ell }_{i}^{2}}\varrho }{E}},{{U}_{3}}={\frac {9g\,{{\ell }_{i}^{2}}\varrho }{2E}}$===Solving=== Text

1+1

tmp

Wir tragen die Ergebnisse für die numerische Näherungslösung gegen die exakte Lösung auf. Dabei setzen wir l_i=l₀/3. Die Verschiebungen sind elementweise für die Elemente e = 1,2,3 aufgetragen:

Verschiebung u(x) - analytische und FE-Lösung

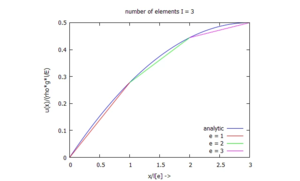
Post-processing

Text

1+1

{{Template:MyTip|title=Spannungen im Stab|text=Tragen Sie auch die Spannungen im Stab über die Stablänge an! Berechnen Sie die Spannungen auf Basis der Dehnung 

$\displaystyle \varepsilon ={\frac {du}{dx}}.$

Links

• ...

Literature

• ...