Gelöste Aufgaben/FEAA: Unterschied zwischen den Versionen
| Zeile 95: | Zeile 95: | ||
|text= | |text= | ||
[[Datei:FEAA-plot.png|mini|Potentielle Energie - hier als Funktion von ''w<sub>1</sub>''.]] | [[Datei:FEAA-plot.png|mini|Potentielle Energie - hier als Funktion von ''w<sub>1</sub>''.]] | ||
Das dimensionslose-gemachte Potential U ist hier | Das dimensionslose-gemachte Potential ''U'' ist hier über ''w<sub>2</sub>'' aufgetragen: man erkennt das Minimum des Potentials bei der berechneten Lösung. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
Version vom 23. Februar 2021, 14:33 Uhr
Aufgabenstellung
Hier geht es darum, ein Verständnis für Näherunglösungen mit dem Prinzip vom Minimum der Potentiellen Energie zu bekommen. Wir suchen die Näherungslösung für die statische Auslenkung des skizzierten Feder-Masse Systems, hier indem wir die Anzahl der Freiheitsgrade von Zwei auf Eins reduzieren.
Und das als Vorbereitung für die Methode der Finiten Elemente, bei der wir die Anzahl der Freiheitsgraden von unendlich auf einige Hundert reduzieren.
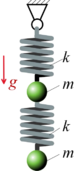
Gesucht ist eine Näherungslösung für die statische Auslenkung der beiden Massen für ein System mit einem Freiheitsgrad. Wir arbeiten dabei mit dem Prinzip vom Minimum der Potentiellen Energie und wählen eine Auslenkung als Funktion der zweiten.
Lösung mit Maxima
Header
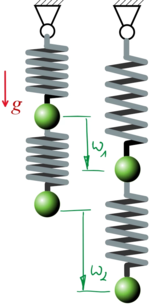
Als Koordinaten führen wir die Auslenkungen der Massen aus Ihrer Referenzlage ein, in der Referenzlage sind die Federn entspannt.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2017-09-14 */
/* ref: FEM, PVMPE using two coordinates */
/* description: solve by principle of minimum of p. E. */
/*******************************************************/
Equlibrium Conditions
Das Potential für das Aufstellen der Gleichgewichtsbeziehung lautet
wobei
/* Potential Energy of system (equilibrium condition) */
parts : [/* work of gravitationaö forces */
A = m*g*w[1]+m*g*w[2],
/* strain energy*/
Pi = 1/2*k*w[1]^2 + 1/2*k*(w[2]-w[1])^2];
PMPE : U= Pi-A;
PMPE : subst(parts,PMPE);
Solving
Um zu zeigen, wie eine Näherungslösung "geht", wählen wir hier einen geschätzten (falschen = nicht analytisch richtigen) Zusammenhang zwischen w1 und w2:
Das Potential 'U' lautet nun
und liefert mit der Gleichgewichtsbeziehung des Prinzips vom Minimum der Potentiellen Energie
- .
die Gleichung
- .
mit der Lösung
/* choose approximation */
approx: [w[1] = w[2]/2];
PMPE: subst(approx, PMPE);
/* pick individual equations */
equ : diff(subst(PMPE, -U),w[2])=0;
/* -> here we employ the shortcut via "solve" */
sol: solve(equ,w[2])[1];
Post-Procesing
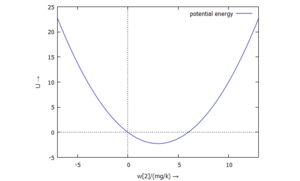
Das dimensionslose-gemachte Potential U ist hier über w2 aufgetragen: man erkennt das Minimum des Potentials bei der berechneten Lösung.
/* plot results */
pltfct : expand(subst([w[2] = m*g/k*W[2]],
subst(approx,subst(parts, subst(PMPE,U/(m^2*g^2/k))))));
plot2d(pltfct,
[W[2],3-10,3+10],
[legend, "potential energy"],
[xlabel, "w[2]/(mg/k) →"], [ylabel, "U →"]);
Links
- ...
Literature
- ...