Gelöste Aufgaben/FEAB: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Category:Randwertproblem]] | |||
[[Datei:FEAB- | [[Category:Gelöste Aufgaben]] | ||
[[Category:Prinzip der virtuellen Verrückungen]] | |||
[[Category:Maxima]] | |||
==Aufgabenstellung== | |||
Statt zwei Freiheitsgraden wie in [[Gelöste_Aufgaben/FEAA|FEAA]] haben wir jetzt - bei einem Kontinuum - unendlich viele. | |||
<onlyinclude> | |||
[[Datei:FEAB-01.png|mini|198x198px|Lageplan]] | |||
Gesucht ist die Näherungslösung für die Auslenkung der Stab-Querschnitte mit dem Prinzip der Virtuellen Verrückungen. Wir verwenden polynomialen Ansatzfunktionen über die Gesamtlänge - also eine Mischung aus [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Finiten-Elemente-Methode]] und dem [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Im Vergleich: das Verfahren von Ritz und die Methode der Finite Elemente|Rayleigh-Ritz-Verfahren]]. | |||
</onlyinclude> | |||
==Lösung mit Maxima== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
[[Datei:FEAB- | <!-------------------------------------------------------------------------------->Für Maxima brauchen wir einige Deklarationen. | ||
Der maximale Exponent des Ansatz-Polynoms ist drei - dann fällt die Näherungslösung mit der analytischen Lösung zusammen. | |||
Hier wählen wir | |||
<math>I=2</math>{{MyCodeBlock|title=Declarations | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->Für die Formfunktionen wählen wir | |||
<math>\displaystyle u(x) = \sum_{i=1}^{I} U_i\cdot \left(\frac{x}{\ell}\right)^i</math>> , | |||
also für I=2 | |||
<math>\displaystyle u(x) = U_1 \frac{x}{l} + U_2 \left(\frac{x}{l}\right)^2</math> | |||
und entsprechend | |||
<math>\displaystyle \delta u(x) = \delta U_1 \frac{x}{l} + \delta U_2 \left(\frac{x}{l}\right)^2</math> .{{MyCodeBlock|title=Formfuctions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->Die Gleichgewichtsbedingung | |||
<math>\begin{array}{ll}\delta W &= \delta W^a - \delta \Pi\\ &\stackrel{!}{=}0\end{array}</math> | |||
liefert | |||
<math>\displaystyle \delta W = \frac{\delta U_{2} A g \ell \rho}{3}+\frac{\delta U_{1} A g \ell \rho}{2} - \frac{4{{U}_{2}}\,{{\mathit{{\delta}U}}_{2}}AE}{3\ell}-\frac{{{U}_{1}}\,{{\mathit{{\delta}U}}_{2}}AE}{\ell}-\frac{{{\mathit{{\delta}U}}_{1}}\,{{U}_{2}}AE}{\ell}-\frac{{{U}_{1}}\,{{\mathit{{\delta}U}}_{1}}A E}{\ell}</math>.{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<!-------------------------------------------------------------------------------->Die Glechgewichtsbedingungen folgen daraus zu | |||
<math>\begin{array}{l}\displaystyle-\frac{A g \ell\rho}{2}+\frac{{{U}_{2}}AE}{\ell}+\frac{{{U}_{1}} A E}{\ell}=0, \\ \displaystyle -\frac{A g \ell \rho}{3}+\frac{4{{U}_{2}}AE}{3l}+\frac{{{U}_{1}}AE}{\ell}=0\end{array}</math> | |||
und somit | |||
<math>\displaystyle {{U}_{1}}=\frac{g\,{{\ell}^{2}}\rho}{E},\;\;\;{{U}_{2}}=-\frac{g\,{{\ell}^{2}}\rho}{2E}</math>{{MyCodeBlock|title=Solving | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<!--------------------------------------------------------------------------------> | |||
Und wir tragen die Ergebnisse auf für die numerische Näherungslösung | |||
<math>\displaystyle u(x) = \frac{g \rho \ell^2}{E} \cdot \frac{x}{\ell} - \frac{g \rho \ell^{2}}{2E} \cdot \left(\frac{x}{\ell}\right)^2</math> | |||
gegen die exakte Lösung auf:[[Datei:FEAB-Ergebnisplot.png|mini|Verschiebung der Stab-Querschnitte.]]{{MyCodeBlock|title=Post-Processing | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
'''Links''' | |||
*... | |||
'''Literature''' | |||
*... | |||
Version vom 23. Februar 2021, 14:28 Uhr
Aufgabenstellung
Statt zwei Freiheitsgraden wie in FEAA haben wir jetzt - bei einem Kontinuum - unendlich viele.
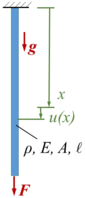
Gesucht ist die Näherungslösung für die Auslenkung der Stab-Querschnitte mit dem Prinzip der Virtuellen Verrückungen. Wir verwenden polynomialen Ansatzfunktionen über die Gesamtlänge - also eine Mischung aus Finiten-Elemente-Methode und dem Rayleigh-Ritz-Verfahren.
Lösung mit Maxima
Header
Text
1+1
Für Maxima brauchen wir einige Deklarationen.
Der maximale Exponent des Ansatz-Polynoms ist drei - dann fällt die Näherungslösung mit der analytischen Lösung zusammen.
Hier wählen wir
===Declarations=== Text
1+1
Für die Formfunktionen wählen wir
> ,
also für I=2
und entsprechend
.===Formfuctions=== Text
1+1
Die Gleichgewichtsbedingung
liefert
.===Equilibrium Conditions=== Text
1+1
Die Glechgewichtsbedingungen folgen daraus zu
und somit
===Solving=== Text
1+1
Und wir tragen die Ergebnisse auf für die numerische Näherungslösung
gegen die exakte Lösung auf:
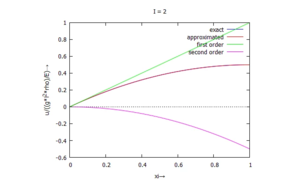
===Post-Processing===
Text
1+1
Links
- ...
Literature
- ...