Gelöste Aufgaben/DGEB: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 35: | Zeile 35: | ||
/* the Timoshenko and EBB beam */ | /* the Timoshenko and EBB beam */ | ||
/*******************************************************/ | /*******************************************************/ | ||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | |||
|text= | |||
Wir brauchen das volle Instrumentarium der Elastizitätstheorie - angefangen bei einfachen Abkürzungen wie der Querschnittsfläche ''A'' bis zu den Flächenmomenten 2. Grades ''I<sub>y</sub>'' und ''I<sub>z</sub>'': | |||
::<math>\begin{array}{ccc} | |||
\displaystyle I_y&=&\frac{b \cdot h^3}{12},\\ | |||
\displaystyle I_z&=&\frac{h \cdot b^3}{12},\\ | |||
\displaystyle A&=&b\cdot h | |||
\end{array}</math> | |||
über Lame's Konstante | |||
::<math>\lambda=\frac{E \cdot \nu}{\left( 1-2 \cdot \nu \right) \cdot \left( \nu+1 \right) }, \mu=\frac{E}{2 \cdot \left( \nu+1 \right) }</math>, | |||
und dem linearen Werkstoffgesetz (Spannungs-Dehnungs-Beziehung / Hook's Gesetz) | |||
::<math>\underline{\underline{E} } = \begin{pmatrix} | |||
2\cdot \mu+\lambda & \lambda & \lambda & 0 & 0 & 0\\ | |||
\lambda & 2\cdot \mu+\lambda & \lambda & 0 & 0 & 0\\ | |||
\lambda & \lambda & 2\cdot \mu+\lambda & 0 & 0 & 0\\ | |||
0 & 0 & 0 & \mu & 0 & 0\\ | |||
0 & 0 & 0 & 0 & \mu & 0\\ | |||
0 & 0 & 0 & 0 & 0 & \mu\\ | |||
\end{pmatrix}</math>. | |||
Und schließlich wollen wir die Verzerrungs-Verscheibungs-Beziehung für einen materiellen Punkt ''P'' angeben. Grundlage ist die Verschiebung eines Punkte ''P=[x,y,z]'' und die gesuchten Koeffizienten ''u, v, w'' der Verschiebung in die drei Raumrichtungen | |||
< | ::<math>\underline{r}_P</math>, | ||
{{ | |||
Die Koeffizienten ''u(x,y,z), v''(x,y,z)'', w''(x,y,z)'''' des Ortsvektors ''r<sub>P</sub>'' beschreiben dabei das Verscheibungsfeld des Balkens. Wir erhalten mit den allgemeinen Komponenten ''u'', ''v'' und ''w'' des Verschiebungsfeldes | |||
::<math>\underline{r}_P = \left(\begin{array}{l}u(x,y,z)\\v(x,y,z)\\w(x,y,z)\end{array}\right)</math> | |||
die Verzerrungen allgemein zu | |||
::<math>\begin{array}{ll} {{\varepsilon}_{x,x}}&=\displaystyle \frac{d}{d\,x}\cdot u\left( x,y,z\right) \\ {{\varepsilon}_{y,y}}&=\displaystyle \frac{d}{d\,y}\cdot v\left( x,y,z\right) \\ {{\varepsilon}_{z,z}}&=\displaystyle \frac{d}{d\,z}\cdot w\left( x,y,z\right) \\ {{\varepsilon}_{x,y}}&=\frac{\displaystyle \frac{d}{d\,y}\cdot u\left( x,y,z\right) +\displaystyle \frac{d}{d\,x}\cdot v\left( x,y,z\right) }{\displaystyle 2}\\ {{\varepsilon}_{x,z}}&=\frac{\displaystyle \frac{d}{d\,z}\cdot u\left( x,y,z\right) +\displaystyle \frac{d}{d\,x}\cdot w\left( x,y,z\right) }{\displaystyle 2}\\ {{\varepsilon}_{y,z}}&=\frac{\displaystyle \frac{d}{d\,z}\cdot v\left( x,y,z\right) +\displaystyle \frac{d}{d\,y}\cdot w\left( x,y,z\right) }{\displaystyle 2} \end{array}</math>. | |||
Damit das "schöner" aussieht,, kürzen wir im Folgenden ab | |||
::<math>\displaystyle \frac{d}{dx}(.) := (.)_x, \;\;\frac{d}{dy}(.) := (.)_y, \;\;\frac{d}{dz}(.) := (.)_z, </math> | |||
und erhalten als Verzerrungs-Verscheibungs-Beziehung | |||
::<math>\begin{array}{ll} {{\varepsilon}_{x,x}}&= u_x \\ {{\varepsilon}_{y,y}}&= v_y \\ {{\varepsilon}_{z,z}}&= w_z \\ {{\varepsilon}_{x,y}}&= \frac{\displaystyle 1}{\displaystyle 2}\left(u_y+v_x \right)\\ {{\varepsilon}_{x,z}}&= \frac{\displaystyle 1}{\displaystyle 2}\left(u_z+w_x \right)\\ {{\varepsilon}_{y,z}}&= \frac{\displaystyle 1}{\displaystyle 2}\left(v_z+w_y \right)\\ \end{array} | |||
</math>. | |||
Für unser Problem suchen wir jetzt ein konkretes Verschiebungsfeld, das unseren Anforderungen an das Problem genügt. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /*******************************************************/ | ||
/* declare variational variables */ | |||
declare("δW", alphabetic); /* virtual work */ | |||
declare("δA", alphabetic); /* virtual work of implied external forces */ | |||
declare("δΠ", alphabetic); /* virtual strain energy */ | |||
declare("δu", alphabetic); /* variation of u */ | |||
declare("δw", alphabetic); | |||
declare("δφ", alphabetic); | |||
declare("δη", alphabetic); | |||
declare("δθ", alphabetic); | |||
declare("λ" , alphabetic); /* otherwise, this is the lambda fct. */ | |||
declare("μ" , alphabetic); | |||
declare("Δr", alphabetic); /*displacement of material point [x,y,z] */ | |||
declare("δΔr",alphabetic); /* variation of Δr */ | |||
declare("δZ", alphabetic); /* variation of strain */ | |||
/*******************************************************/ | |||
/* parameters */ | |||
/* abbreviate: */ | |||
geometry : [h^3 = 12*I[y]/b, b^3 = 12*I[z]/h, b = A/h]; | |||
/* Lame's Constants */ | |||
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */ | |||
lameConst : [λ = e*nu/((1+nu)*(1-2*nu)), μ = e/(2*(1+nu))]; | |||
/* relation: hook's law, modulus of elasticity */ | |||
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */ | |||
E : matrix([2*μ+λ, λ, λ, 0, 0, 0], | |||
[ λ, 2*μ+λ, λ, 0, 0, 0], | |||
[ λ, λ, 2*μ+λ, 0, 0, 0], | |||
[ 0, 0, 0, μ, 0, 0], | |||
[ 0, 0, 0, 0, μ, 0], | |||
[ 0, 0, 0, 0, 0, μ]); | |||
/* Strain Displacement Relation */ | |||
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */ | |||
StrainDispl(arg) := [epsilon[x,x] = diff(arg[1],x), | |||
epsilon[y,y] = diff(arg[2],y), | |||
epsilon[z,z] = diff(arg[3],z), | |||
epsilon[x,y] = 1/2*(diff(arg[1],y) + diff(arg[2],x)), | |||
epsilon[x,z] = 1/2*(diff(arg[1],z) + diff(arg[3],x)), | |||
epsilon[y,z] = 1/2*(diff(arg[2],z) + diff(arg[3],y))]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
Version vom 23. Februar 2021, 10:05 Uhr
Aufgabenstellung
In dieser Aufgabe starten wir von "first principles" - hier das Prinzip der virtuellen Verrückungen - und entwicklen die Bewegungsgleichunge für einen schlanken Stab unter Langskräft und Biegemoment.
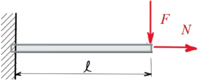
Gesucht sind die Differentialgleichungen des statischen Gleichgewichts für den schlanken Stab mit Rechteck-Querschnitt unter Längs- und Querkraft, ausgehend von der Virtuellen Formänderungsenergie δΠ.
Wir finden so die bekannten Differentialbeziehungen für das Timoshenko / Euler-Bernoulli-Modell eines Balkens.
Lösung mit Maxima
Wie alle zentralen Begriffe der Elastizitätstheorie ineinandergreifen, um die virtuelle Formänderungsenergie für den Euler-Bernoulli-Balken zu ermitteln, zeigt diese Aufgabe.
Header
Hier kommen
- das Hook'sche Gesetz in seiner allgemeinen, 3D-Fassung,
- die allgemeinen Verschiebungs-Verzerrungs-Bedingungen,
- die klassischen Annahmen zur Theorie von Stäben zum Einsatz sowie
- die Gleichgewichtsbedingungen nach dem Prinzip der virtuellen Verrückungen.
zum Einsatz.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2016-03-27 */
/* ref: Euler-Bernoulli Beam */
/* description: derives the equations of motion for */
/* the Timoshenko and EBB beam */
/*******************************************************/
Declarations
Wir brauchen das volle Instrumentarium der Elastizitätstheorie - angefangen bei einfachen Abkürzungen wie der Querschnittsfläche A bis zu den Flächenmomenten 2. Grades Iy und Iz:
über Lame's Konstante
- ,
und dem linearen Werkstoffgesetz (Spannungs-Dehnungs-Beziehung / Hook's Gesetz)
- .
Und schließlich wollen wir die Verzerrungs-Verscheibungs-Beziehung für einen materiellen Punkt P angeben. Grundlage ist die Verschiebung eines Punkte P=[x,y,z] und die gesuchten Koeffizienten u, v, w der Verschiebung in die drei Raumrichtungen
- ,
Die Koeffizienten u(x,y,z), v(x,y,z), w(x,y,z)' des Ortsvektors rP beschreiben dabei das Verscheibungsfeld des Balkens. Wir erhalten mit den allgemeinen Komponenten u, v und w des Verschiebungsfeldes
die Verzerrungen allgemein zu
- .
Damit das "schöner" aussieht,, kürzen wir im Folgenden ab
und erhalten als Verzerrungs-Verscheibungs-Beziehung
- .
Für unser Problem suchen wir jetzt ein konkretes Verschiebungsfeld, das unseren Anforderungen an das Problem genügt.
/*******************************************************/
/* declare variational variables */
declare("δW", alphabetic); /* virtual work */
declare("δA", alphabetic); /* virtual work of implied external forces */
declare("δΠ", alphabetic); /* virtual strain energy */
declare("δu", alphabetic); /* variation of u */
declare("δw", alphabetic);
declare("δφ", alphabetic);
declare("δη", alphabetic);
declare("δθ", alphabetic);
declare("λ" , alphabetic); /* otherwise, this is the lambda fct. */
declare("μ" , alphabetic);
declare("Δr", alphabetic); /*displacement of material point [x,y,z] */
declare("δΔr",alphabetic); /* variation of Δr */
declare("δZ", alphabetic); /* variation of strain */
/*******************************************************/
/* parameters */
/* abbreviate: */
geometry : [h^3 = 12*I[y]/b, b^3 = 12*I[z]/h, b = A/h];
/* Lame's Constants */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
lameConst : [λ = e*nu/((1+nu)*(1-2*nu)), μ = e/(2*(1+nu))];
/* relation: hook's law, modulus of elasticity */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
E : matrix([2*μ+λ, λ, λ, 0, 0, 0],
[ λ, 2*μ+λ, λ, 0, 0, 0],
[ λ, λ, 2*μ+λ, 0, 0, 0],
[ 0, 0, 0, μ, 0, 0],
[ 0, 0, 0, 0, μ, 0],
[ 0, 0, 0, 0, 0, μ]);
/* Strain Displacement Relation */
/* see https://en.wikipedia.org/wiki/Hooke%27s_law */
StrainDispl(arg) := [epsilon[x,x] = diff(arg[1],x),
epsilon[y,y] = diff(arg[2],y),
epsilon[z,z] = diff(arg[3],z),
epsilon[x,y] = 1/2*(diff(arg[1],y) + diff(arg[2],x)),
epsilon[x,z] = 1/2*(diff(arg[1],z) + diff(arg[3],x)),
epsilon[y,z] = 1/2*(diff(arg[2],z) + diff(arg[3],y))];
Euler Rotation
Text
1+1
Stress-Strain-Relations for a Rod
Text
1+1
Displacement Variables
Text
1+1
Virtual Strain Energy
Text
1+1
Timoshenko-Beam
Text
1+1
Euler-Bernoulli-Balken
Text
1+1
Links
- ...
Literature
- ...