Anfangswertprobleme/Methoden zur Lösung von Anfangswertproblemen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
== Problemstellung == | |||
Fast immer sind im Maschinenbau Anfangswertprobleme über Differentialgleichungen im Zeitbereich definiert - die unabhängige Koordinate ist deshalb hier immer ''t''. Für die gesuchte Funktion | |||
<math>\displaystyle q(t) \text{ und der Abkürzung } \frac{d}{dt}(.):=\dot{(.)}</math> | |||
suchen wir die Lösung zum Anfangswertproblem<math>\dot{q} = f(q,t) \text{ mit dem Anfangswert } q(0) = q_0</math> | |||
im Zeitintervall 0 ''< t < T''. | |||
Numerische Löser für Anfangswertprobleme gibt es meist nur für Differentialgleichungen erster Ordnung (erste Ableitung nach der Zeit). Da Bewegungsgleichungen mechanischer Systeme fast immer Differentialgleichungen zweiter Ordnung sind (die Beschleunigung und damit die d'Alembert'sche Trägheitskrafte sind zweite Ableitungen des Weges nach der Zeit), brauchen wir einen Trick: Wir führen die Geschwindigkeit explizit als Koordinate ein, z.B. für die Bewegungsgleichung | |||
<math>\ddot{u}(t) = f(u,\dot{u},t)</math> | |||
Nun sind | |||
<math>u, \dot{u}</math> | |||
die Zustandsgrößen des Systems. | |||
Mit | |||
<math>v(t) = \dot{u}(t)</math> | |||
schreiben wir die Differentialgleichung zweiter Ordnung als zwei Differentialgleichungen erster Ordnung: | |||
<math>\underbrace{\left(\begin{array}{c}\dot{v}\\\dot{u}\end{array}\right)}_{\displaystyle \underline{\dot{q}}} = \underbrace{\left(\begin{array}{c}f(u, v, t)\\v\end{array}\right)}_{\displaystyle \underline{f}(\underline{q},t)}</math> | |||
== Beispiel 1: Wachstum einer Population == | |||
Eine Fliegenpopulation besteht zum Zeitpunkt ''t=0'' aus der Anzahl von ''n<sub>0</sub>'' Fliegen. | |||
In einem Zeitintervall stirbt ein Anteil ''λ<sub>S</sub>'' von Fliegen, ein Anteil ''λ<sub>G</sub>'' von Fliegen wird geboren, das Anfangswertproblem lautet: | |||
<math>\dot{n} = \underbrace{(\lambda_G-\lambda_S )}_{\displaystyle =: \lambda_0} \cdot n\; \text{ mit dem Anfangswert } n(0) = n_0</math> | |||
Die analytische Lösung dazu ist | |||
<math>\displaystyle n(t) = n_0 \cdot e^{\lambda_0\cdot t}</math> | |||
== Beispiel 2: Wachstum einer Population mit Selbstvergiftung == | |||
Für sehr viele Fliegen ''n'' führen dies zu "Wachstum mit Selbstvergiftung". Die Stoffwechselrückstände ''r'' der Population in einem abgeschlossenen System (z.B. Erde) führen zum Aufbau von Hemmstoffen, die negativ auf die Geburtenrate ''λ<sub>G</sub>'' wirken, hier mit dem Faktor ''(1-r)''. | |||
Dieses Modell (die Bewegungsgleichung) für ''r'' setzt für die Änderungsgeschwindigkeit einen Prozess an, bei dem die Hemmstoffe | |||
* proportional mit ''μ'' zur Anzahl der Fliegen ''n'' steigen und | |||
* proportional zu ''r'' abgebaut werden (zerfallen):<math>\begin{array}{ll}\dot{n} &= \left(\lambda_G\cdot(1-r)-\lambda_S\right) \cdot n\\ \dot{r} &= \mu \cdot n -\varrho\cdot r\end{array}\; \text{ mit den Anfangswerten } n(0) = n_0, r(0) = 0</math> | |||
Klimamodelle machen genau das - nur mit deutlich komplizierteren Modellen. | |||
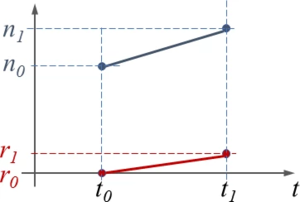
[[Datei:MethodenAnfangswertprobleme-Euler.png|ohne|mini|Integrationsschritt beim Lösen eines AWPs.]] | [[Datei:MethodenAnfangswertprobleme-Euler.png|ohne|mini|Integrationsschritt beim Lösen eines AWPs.]] | ||
| Zeile 11: | Zeile 59: | ||
'''Links''' | '''Links''' | ||
* [[Sources/Lexikon/Phasendiagramme|Phasendiagramme]] | * [[Sources/Lexikon/Phasendiagramme|Phasendiagramme]]: eine Methode zum Ausdeuten der Lösung von nunmerisch gelösten AWP. | ||
Version vom 22. Februar 2021, 11:18 Uhr
Problemstellung
Fast immer sind im Maschinenbau Anfangswertprobleme über Differentialgleichungen im Zeitbereich definiert - die unabhängige Koordinate ist deshalb hier immer t. Für die gesuchte Funktion
suchen wir die Lösung zum Anfangswertproblem
im Zeitintervall 0 < t < T.
Numerische Löser für Anfangswertprobleme gibt es meist nur für Differentialgleichungen erster Ordnung (erste Ableitung nach der Zeit). Da Bewegungsgleichungen mechanischer Systeme fast immer Differentialgleichungen zweiter Ordnung sind (die Beschleunigung und damit die d'Alembert'sche Trägheitskrafte sind zweite Ableitungen des Weges nach der Zeit), brauchen wir einen Trick: Wir führen die Geschwindigkeit explizit als Koordinate ein, z.B. für die Bewegungsgleichung
Nun sind
die Zustandsgrößen des Systems.
Mit
schreiben wir die Differentialgleichung zweiter Ordnung als zwei Differentialgleichungen erster Ordnung:
Beispiel 1: Wachstum einer Population
Eine Fliegenpopulation besteht zum Zeitpunkt t=0 aus der Anzahl von n0 Fliegen.
In einem Zeitintervall stirbt ein Anteil λS von Fliegen, ein Anteil λG von Fliegen wird geboren, das Anfangswertproblem lautet:
Die analytische Lösung dazu ist
Beispiel 2: Wachstum einer Population mit Selbstvergiftung
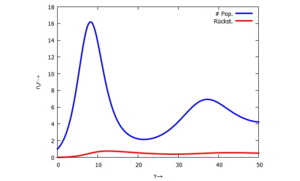
Für sehr viele Fliegen n führen dies zu "Wachstum mit Selbstvergiftung". Die Stoffwechselrückstände r der Population in einem abgeschlossenen System (z.B. Erde) führen zum Aufbau von Hemmstoffen, die negativ auf die Geburtenrate λG wirken, hier mit dem Faktor (1-r).
Dieses Modell (die Bewegungsgleichung) für r setzt für die Änderungsgeschwindigkeit einen Prozess an, bei dem die Hemmstoffe
- proportional mit μ zur Anzahl der Fliegen n steigen und
- proportional zu r abgebaut werden (zerfallen):
Klimamodelle machen genau das - nur mit deutlich komplizierteren Modellen.
Links
- Phasendiagramme: eine Methode zum Ausdeuten der Lösung von nunmerisch gelösten AWP.
Untergeordnete Seiten