Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode/FEM: Trial-Functions für lineare Ansatz-Polynome: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
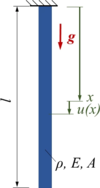
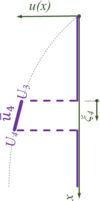
Stabmodell im Erdschwerefeld.
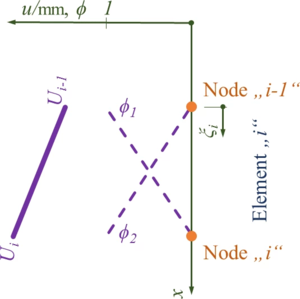
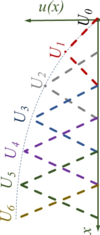
Überlagerung der Trial-Functions.
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 7: | Zeile 7: | ||
Dafür ist dieses Beispiel (aus [[Gelöste Aufgaben/FEAB|FEAB]]): | Dafür ist dieses Beispiel (aus [[Gelöste Aufgaben/FEAB|FEAB]]): | ||
[[Datei:FEM-lineareTrialFcts-Stabmodell.png| | [[Datei:FEM-lineareTrialFcts-Stabmodell.png|100px|left|mini|Stabmodell im Erdschwerefeld.]] | ||
Ein dehnbarer Stab ist an der "Decke" im Erd-Schwerefeld aufgehängt. Der Stab hat die Dehnsteifigkeit EA, die Dichte ρ und die Gesmtlänge l. | Ein dehnbarer Stab ist an der "Decke" im Erd-Schwerefeld aufgehängt. Der Stab hat die Dehnsteifigkeit EA, die Dichte ρ und die Gesmtlänge l. | ||
Gesucht ist eine Approximation der Auslenkung u(x). | Gesucht ist eine Approximation der Auslenkung u(x). | ||
<br clear="all"/> | |||
<table class="wikitable"> | <table class="wikitable"> | ||
<tr><th>STEP A</th><th>B</th><th>C</th><th>D</th><th>E</th></tr> | <tr><th width="20%">STEP A</th><th width="20%">B</th><th width="20%">C</th><th width="20%">D</th><th>E</th></tr> | ||
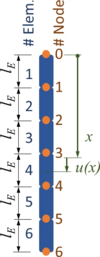
<td>[[Datei:FEM-linearTrialFcts-introduction.png|mini|Einführung der Trial-Functions]]</td> | <td colspan="5">[[Datei:FEM-linearTrialFcts-introduction.png|mini|Einführung der Trial-Functions]]</td> | ||
</table> | </table> | ||
Version vom 22. Februar 2021, 08:29 Uhr
Auch wenn es so aussieht, als wäre alles zur FEM gesagt, sind die Trial-Funktionen der FEM eine besondere Delikatesse!
Wie bei allen wirklichen Delikatessen steht vor dem Genuss noch etwas Arbeit, denn:
Es gibt einen Trick, wie diese Trial-Funktionen aussehen, damit wir Sie am Rechner einfach zusammenbauen können.
Dafür ist dieses Beispiel (aus FEAB):

Ein dehnbarer Stab ist an der "Decke" im Erd-Schwerefeld aufgehängt. Der Stab hat die Dehnsteifigkeit EA, die Dichte ρ und die Gesmtlänge l.
Gesucht ist eine Approximation der Auslenkung u(x).
| STEP A | B | C | D | E |
|---|---|---|---|---|
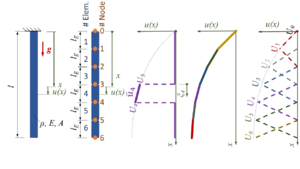 |
||||

 |
 |
 |
 |
 |