Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Integration der Differentialbeziehung (EBB): Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 14: | Zeile 14: | ||
* die Knoten des Balkens (die Black-Boxen im Bild), hier ''A, B, C, D ... Y'' und ''Z.'' | * die Knoten des Balkens (die Black-Boxen im Bild), hier ''A, B, C, D ... Y'' und ''Z.'' | ||
[[Datei:IntegrationDerDifferentialbeziehung-Übergänge.png|left|mini|Felder sowie Rand- und Übergangsbedingungen.]]<br clear="all"/> | [[Datei:IntegrationDerDifferentialbeziehung-Übergänge.png|587px|left|mini|Felder sowie Rand- und Übergangsbedingungen.]]<br clear="all"/> | ||
Hier sind die Balken - der Einfachheit-halber - in einer Linie hintereinander angeordnet. | Hier sind die Balken - der Einfachheit-halber - in einer Linie hintereinander angeordnet. | ||
| Zeile 29: | Zeile 29: | ||
::<math>E_i I_i w''''(x_i) =q_i(x_i)</math>. | ::<math>E_i I_i w''''(x_i) =q_i(x_i)</math>. | ||
[[Datei:IntegrationDerDifferentialbeziehung-Streckenlast.png|left|mini|Koordinaten der Streckenlast ''q(x)''.]]<br clear="all"/> | [[Datei:IntegrationDerDifferentialbeziehung-Streckenlast.png|200px|left|mini|Koordinaten der Streckenlast ''q(x)''.]]<br clear="all"/> | ||
Diese Differentialgleichung können wir zur Biegelinie ''w(x)'' integrieren und erhalten | Diese Differentialgleichung können wir zur Biegelinie ''w(x)'' integrieren und erhalten | ||
| Zeile 111: | Zeile 111: | ||
gelenkiges Festlager | gelenkiges Festlager | ||
|- | |- | ||
|[[Datei:IntegrationDerDifferentialbeziehung-Rand-1.png|Rand-Knoten]] | |[[Datei:IntegrationDerDifferentialbeziehung-Rand-1.png|100px|Rand-Knoten]] | ||
|[[Datei:IntegrationDerDifferentialbeziehung-Rand-Beispiel.png|Gelenkiges Lager und Schnittgrößen.]] | |[[Datei:IntegrationDerDifferentialbeziehung-Rand-Beispiel.png|100px|Gelenkiges Lager und Schnittgrößen.]] | ||
|} | |} | ||
Für ein gelenkiges Festlager kommen die zwei Gleichungen aus | Für ein gelenkiges Festlager kommen die zwei Gleichungen aus | ||
| Zeile 139: | Zeile 139: | ||
Gelenk | Gelenk | ||
|- | |- | ||
|[[Datei:IntegrationDerDifferentialbeziehung-Übergang.png|mini|Übergangs-Knoten.]] | |[[Datei:IntegrationDerDifferentialbeziehung-Übergang.png|100px|mini|Übergangs-Knoten.]] | ||
|[[Datei:IntegrationDerDifferentialbeziehung-Übergang-Beispiel.png|mini|Übergangs-Knoten, Beispiel: Gelenk]] | |[[Datei:IntegrationDerDifferentialbeziehung-Übergang-Beispiel.png|100px|mini|Übergangs-Knoten, Beispiel: Gelenk]] | ||
|} | |} | ||
Für ein Gelenk kommen die vier Gleichungen aus | Für ein Gelenk kommen die vier Gleichungen aus | ||
Version vom 19. Februar 2021, 15:35 Uhr
Das Randwertproblem eines Euler-Bernoulli-Balkens können wir durch
- Integration der Differentialbeziehung im Feld (der Biege-Differentialgleichung EI w'''' = q) und
- Anpassen der Integrationsbedingungen an die Rand- und Übergangs-Bedingungen an den Knoten
lösen.
Das Integral für w der Feld-Differentialgleichung ist die allgemeine Lösung: das w(x) ist unabhängig von dern Rändern des Feldes aber spezifisch für die Last q(x). Das problem-spezifische w(x) erhalten wir an, indem wir die allgemeine Lösung mit Ihren Integrationskonstanten an die Randbedingungen anpassen.
Aufteilung in Felder und Knoten
Zum Randwertproblem gehören
- die Felder, hier I, II, III, .... X und
- die Knoten des Balkens (die Black-Boxen im Bild), hier A, B, C, D ... Y und Z.
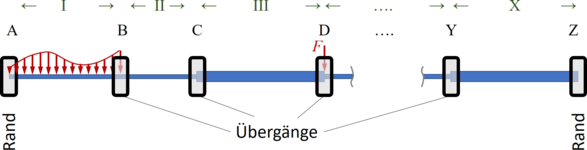
Hier sind die Balken - der Einfachheit-halber - in einer Linie hintereinander angeordnet.
Felder
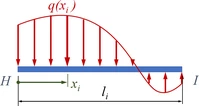
Felder sind Balkenabschnitte zwischen zwei Knoten - als Beispiel hier H und I.
In diesen Bereichen führen wir eine lokale Koordinate xi ein. Hier gilt für 0 < xi < li eine Lösung der Biege-Differentialgleichung
und damit meist - wenn wir mit Balken mit konstantem EI arbeiten
- .
Diese Differentialgleichung können wir zur Biegelinie w(x) integrieren und erhalten
und dabei immer - je Bereich:
- vier Integrationsvariablen, hier Ci0 ... Ci3 .
Das Problem:
- die Integration der Differentialbeziehung glückt fast nur für Probleme, die im Rahmen des Unterrichts der Technischen Mechanik relevant sind. Praktische Probleme lassen sich so fast nie lösen.
Das liegt nicht daran, dass die Integration von qi(xi) scheitert, sondern dass praktische Probleme meist Schalen- oder Volumen-Körper mit komplizierteren Differentialbeziehungen beinhalten oder die Anpassung an die Randbedingungen nicht gelingt.
Knoten
Zwischen zwei Knotenpunkten gilt eine Lösung der Biege-Differentialgleichung. Die Lösung der Biege-Differentialgleichung zweier Bereiche unterscheidet sich durch die Lösung des unbestimmten Integrals
(falls die qi unterschiedlich sind) und die Werte der Integrationskonstanten Cij.
Knotenpunkte sind
- beide Ränder des Balkens,
- Lager und Gelenke,
- Last-Einleitungspunkte für diskrete (punktuelle) Kräfte und Momente sowie
- Unstetigkeiten der Biegesteifigkeit EI oder der Streckenlast qi(xi).
An jedem Knotenpunkt xK = 0 oder xK = ℓi eines Bereichs können wir aus Rand- und Übergangs-Bedingungen Gleichungen für die Anpassung der Integrationskonstanten Cij der Biegelinie gewinnen. Und es müssen je Bereich vier Gleichungen sein.
Dies sind für einen Knoten K
| Rand- bzw. Übergangs-Bedingungen für .... | |
|---|---|
| ❔ | Auslenkung wK |
| ❔ | Neigung w'K |
| ❔ | Schnitt-Moment MK = -EI w''K |
| ❔ | Schnitt-Querkraft QK = -EI w'''K |
Aus Überlegungen zur Arbeit sind diese Bedingungen bei Lagern und Gelenken miteinander verknüpft. Dabei spielen jeweils die Paare [wK, QK] (Weg*Kraft) sowie [w'K, MK] (Drehung*Moment) eine Rolle.
So können wir
- bei Lagern, die wK = 0 erzwingen, keine Randbedingungen aus dem Kräftegleichgewicht in Richtung von w gewinnen,
- bei Lagern, die w'K = 0 erzwingen, keine Randbedingungen aus dem Momentengleichgewicht in Drehrichtung von w' gewinnen,
- bei Lagern, die QK = 0 erzwingen, keine Randbedingungen für die Auslenkung von wK gewinnen sowie
- bei Lagern, die MK = 0 erzwingen, keine Randbedingungen für die Drehung von w'K gewinnen.
Für jeden Rand-Knoten gewinnen wir zwei, für jeden Übergangs-Knoten vier gewöhnliche Gleichungen.
Dies sind
- geometrische Bedingungen und
- Kraft- / Momenten-Gleichgewichtsbedingungen.
Während wir die geometrischen Bedingungen einfach aus dem Lagertyp "ablesen" können, brauchen wir für die Kraft- / Momenten-Gleichgewichtsbedingungen ein Freikörperbild am Knoten.
Da wir an jedem Knoten eine "linke" und eine "rechte" Seite haben, führen wir als Kennzeichnung
- für die "rechte" Seite ein "+" und
- für die "linke" Seite eine"-"
ein.
Rand-Knoten:
| Allgemeines Schnittbild
für einen Rand-Knoten |
Bsp: Schnittbild für ein
gelenkiges Festlager |
|---|---|
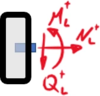
|
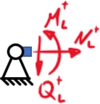
|
Für ein gelenkiges Festlager kommen die zwei Gleichungen aus
| Rand-Bedingungen für .... | |
|---|---|
| ✔ | Auslenkung wK'+ = 0 |
| ❌ | Neigung w'K'+': keine Bedingung |
| ✔ | Schnitt-Moment MK'+'= 0 |
| ❌ | Schnitt-Querkraft QK+': keine Bedingung |
Übergangs-Knoten
| Allgemeines Schnittbild
für einen Übergangs-Knoten |
Schnittbild für ein
Gelenk |
|---|---|
 |
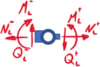 |
Für ein Gelenk kommen die vier Gleichungen aus
| Übergangs-Bedingungen für .... | |
|---|---|
| ✔ | Auslenkung wK'+'= wK- |
| ❌ | Neigung w'K : keine Bedingung |
| ✔
✔ |
Schnitt-Moment MK'+'= 0 und MK-= 0 |
| ✔ | Schnitt-Querkraft QK'+'= QK- |
Links
- Lernvideo T6C0