Gelöste Aufgaben/StaB: Unterschied zwischen den Versionen
Copy from Windows |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[ | [[Kategorie:Gelöste Aufgaben]] | ||
[[ | [[Kategorie:A*x=b]] | ||
[[ | [[Kategorie:Analytische Lösung]] | ||
[[ | [[Kategorie:Randwertproblem]] | ||
[[ | [[Kategorie:Stab]] | ||
[[ | [[Kategorie:Dehnstab]] | ||
[[ | [[Kategorie:Euler-Bernoulli-Balken]] | ||
[[ | [[Kategorie:Geometrische Zwangsbedingung]] | ||
[[ | [[Kategorie:Koordinaten]] | ||
[[ | [[Kategorie:Maxima]] | ||
[[Kategorie:Stabwerk]] | |||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
| Zeile 18: | Zeile 19: | ||
[[Datei:TkPb-01.png|100px|left|mini|Caption]] | [[Datei:TkPb-01.png|100px|left|mini|Caption]] | ||
Gesucht ist ein Vergleich zwischen der klassischen Stabwerkstheorie und einer Herangehensweise, bei der wir eine feste Verbindung der Stäbe in den Knoten ansetzten. | Gesucht ist ein Vergleich zwischen der klassischen Stabwerkstheorie und einer Herangehensweise, bei der wir eine feste Verbindung der Stäbe in den Knoten ansetzten. | ||
</onlyinclude>In der klassischen Stabwerkstheorie (rechts) werden nur die Stab-Längskräfte berücksichtigt – das Ersatzmodell bildet die Verbindungen der Stäbe durch Gelenke ab. Trotzdem wurden die Stäbe in der Ausführung mit Knotenblechen vernietet oder verschweißt – von Gelenk also keine Spur. | </onlyinclude> | ||
[[Datei:TkPb-01.png|100px|right|mini|Caption]] | |||
In der klassischen Stabwerkstheorie (rechts) werden nur die Stab-Längskräfte berücksichtigt – das Ersatzmodell bildet die Verbindungen der Stäbe durch Gelenke ab. Trotzdem wurden die Stäbe in der Ausführung mit Knotenblechen vernietet oder verschweißt – von Gelenk also keine Spur. | |||
Wir untersuchen, welchen Einfluss diese Vereinfachung auf die berechneten Belastungen der Struktur hat. Hier sollen die beiden Modell-Varianten – also die Modellierung mit Gelenken einerseits und Knotenblechen andererseits – miteinander verglichen werden. Gesucht ist die analytische Lösung der beiden Randwertprobleme und ein Vergleich. | Wir untersuchen, welchen Einfluss diese Vereinfachung auf die berechneten Belastungen der Struktur hat. Hier sollen die beiden Modell-Varianten – also die Modellierung mit Gelenken einerseits und Knotenblechen andererseits – miteinander verglichen werden. Gesucht ist die analytische Lösung der beiden Randwertprobleme und ein Vergleich. | ||
| Zeile 26: | Zeile 29: | ||
=== Declarations === | === Declarations === | ||
[[Datei:TkPb-01.png|100px|right|mini|Caption]] | |||
Wir beginnen mit der Einführung von passenden Bezeichnungen für unser System: | Wir beginnen mit der Einführung von passenden Bezeichnungen für unser System: | ||
In Knoten ''I'' und ''II'' sind gelenkige Lager. Stäbe 1,2 und 3 sind im Knoten ''III'' verbunden, Stäbe 2 und 4 im Knoten ''II'' und Stäbe 3 und 4 im Knoten ''IV''. | In Knoten ''I'' und ''II'' sind gelenkige Lager. Stäbe 1,2 und 3 sind im Knoten ''III'' verbunden, Stäbe 2 und 4 im Knoten ''II'' und Stäbe 3 und 4 im Knoten ''IV''. | ||
[[Datei:TkPb-01.png|100px|left|mini|Caption]] | |||
Jeder Stab – hier Stab ''k'' mit den Knoten ''I'' und ''J'' – trägt sein eigenes ''x<sub>k</sub>, z<sub>k</sub>'' – Koordinatensystem und ist im Winkel ''α<sub>k</sub>'' zur Horizontalen eingebaut. Hier sind α<sub>2</sub> = 60° und α<sub>3</sub> = -60° sowie α<sub>1</sub> = 0 und α<sub>4</sub> = 0. | Jeder Stab – hier Stab ''k'' mit den Knoten ''I'' und ''J'' – trägt sein eigenes ''x<sub>k</sub>, z<sub>k</sub>'' – Koordinatensystem und ist im Winkel ''α<sub>k</sub>'' zur Horizontalen eingebaut. Hier sind α<sub>2</sub> = 60° und α<sub>3</sub> = -60° sowie α<sub>1</sub> = 0 und α<sub>4</sub> = 0. | ||
Als Systemparameter je Stab definieren wir vier Stablängen und die jeweils identischen Steifigkeiten für Dehnung und Biegung. Der Querschnitt der Stäbe sei ein doppeltsymmetrisches Profil mit der Querschnittsfläche | Als Systemparameter je Stab definieren wir vier Stablängen und die jeweils identischen Steifigkeiten für Dehnung und Biegung. Der Querschnitt der Stäbe sei ein doppeltsymmetrisches Profil mit der Querschnittsfläche <math>A = a^2</math> und dem Flächenmoment <math>I=\eta \frac{A^2}{12}</math>. | ||
Für das Referenzmodell, das unser System als Stabwerk mit gelenkigen Verbindungen erfasst, wählen wir die Stabkräfte ''S<sub>i</sub>'' als Zugkräfte und schreiben folgende Gleichgewichtsbedingungen an: | Für das Referenzmodell, das unser System als Stabwerk mit gelenkigen Verbindungen erfasst, wählen wir die Stabkräfte ''S<sub>i</sub>'' als Zugkräfte und schreiben folgende Gleichgewichtsbedingungen an: | ||
::<math> | |||
\frac{{S_3}}{2}\operatorname{-}\frac{{S_2}}{2}\operatorname{-}{S_1}\operatorname{=}0\operatorname{,}\operatorname{-}\left( \frac{\sqrt{3} {S_3}}{2}\right) \operatorname{-}\frac{\sqrt{3} {S_2}}{2}\operatorname{=}0\operatorname{,}\operatorname{-}{S_4}\operatorname{-}\frac{{S_3}}{2}\operatorname{=}0\operatorname{,}F\operatorname{-}\frac{\sqrt{3} {S_3}}{2}\operatorname{=}0 | |||
</math> | |||
Die Stabkräfte dazu sind | Die Stabkräfte dazu sind | ||
::<math>{S_1}\operatorname{=}\frac{2 F}{\sqrt{3}}\operatorname{,}{S_2}\operatorname{=}\operatorname{-}\left( \frac{2 F}{\sqrt{3}}\right) \operatorname{,}{S_3}\operatorname{=}\frac{2 F}{\sqrt{3}}\operatorname{,}{S_4}\operatorname{=}\operatorname{-}\left( \frac{F}{\sqrt{3}}\right)</math>. | |||
== Das Randwertproblem == | |||
=== Die Lösung der Felddifferentialgleichung === | === Die Lösung der Felddifferentialgleichung === | ||
Version vom 21. Oktober 2024, 05:02 Uhr
Aufgabenstellung
Wir untersuchen die Belastung eines ebenen Stabwerks. Die Stäbe haben wie skizziert die Länge ℓ bzw. ℓ/2.
Die Struktur wird mit der Kraft F belastet.
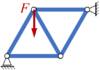
Gesucht ist ein Vergleich zwischen der klassischen Stabwerkstheorie und einer Herangehensweise, bei der wir eine feste Verbindung der Stäbe in den Knoten ansetzten.

In der klassischen Stabwerkstheorie (rechts) werden nur die Stab-Längskräfte berücksichtigt – das Ersatzmodell bildet die Verbindungen der Stäbe durch Gelenke ab. Trotzdem wurden die Stäbe in der Ausführung mit Knotenblechen vernietet oder verschweißt – von Gelenk also keine Spur.
Wir untersuchen, welchen Einfluss diese Vereinfachung auf die berechneten Belastungen der Struktur hat. Hier sollen die beiden Modell-Varianten – also die Modellierung mit Gelenken einerseits und Knotenblechen andererseits – miteinander verglichen werden. Gesucht ist die analytische Lösung der beiden Randwertprobleme und ein Vergleich.
Lösung mit Maxima
Wir nutzen das Computer-Algebra-System Maxima zur Lösung. Das macht Sinn, weil wir eine große Anzahl von Gleichungen verwalten müssen.
Declarations

Wir beginnen mit der Einführung von passenden Bezeichnungen für unser System:
In Knoten I und II sind gelenkige Lager. Stäbe 1,2 und 3 sind im Knoten III verbunden, Stäbe 2 und 4 im Knoten II und Stäbe 3 und 4 im Knoten IV.

Jeder Stab – hier Stab k mit den Knoten I und J – trägt sein eigenes xk, zk – Koordinatensystem und ist im Winkel αk zur Horizontalen eingebaut. Hier sind α2 = 60° und α3 = -60° sowie α1 = 0 und α4 = 0.
Als Systemparameter je Stab definieren wir vier Stablängen und die jeweils identischen Steifigkeiten für Dehnung und Biegung. Der Querschnitt der Stäbe sei ein doppeltsymmetrisches Profil mit der Querschnittsfläche und dem Flächenmoment .
Für das Referenzmodell, das unser System als Stabwerk mit gelenkigen Verbindungen erfasst, wählen wir die Stabkräfte Si als Zugkräfte und schreiben folgende Gleichgewichtsbedingungen an:
Die Stabkräfte dazu sind
- .
Das Randwertproblem
Die Lösung der Felddifferentialgleichung
Wenn wir die Stäbe in den Knotenpunkten fest verbinden, wird das System statisch überbestimmt – wir müssen die Verformungen des Systems berücksichtigen. Durch die geometrische Anordnung der Stäbe sind die Längs- und Querverformung der vier Stäbe miteinander gekoppelt. Wir müssen also zwei Differentialbeziehungen berücksichtigen:
· in Stab-Längsrichtung mit uk(xk) und
· wk(xk) in Stab-Querrichtung.
Für Stab 3 sieht dies folgendermaßen aus:
Die Differentialbeziehungen des Gleichgewichts in u und w sowie deren Lösungen für unsere Stäbe sind
| EI wIIII = 0 | EA u‘‘ = 0 |
mit den Lösungen
| Wk‘‘‘(xk) = …
wobei für den Kippwinkel wk‘(x) := phik(xk) gilt. |
Die Schnittkräfte im Stab ergeben sich dann aus
| Qk(xk) =
Mk(xk) = |
Nk(xk) |
Diese Schnittgrößen jeweils am positiven und negativen Schnittufer sind hier dargestellt:
Randbedingungen: Kinematische Verträglichkeit der Knotenverschiebungen
In den Knoten hat jetzt jeder Stab nun seine eigenen, lokalen Koordinaten der Verschiebung Ui,k, Wik, wobei i den Knoten und k den Stab indexiert.
Damit diese Koordinaten miteinander verträglich sind, führen wir ein Referenzsystem „0“ mit den entsprechenden Koordinaten der Auslenkung in horizontale und vertikale Richtung ein:
Diese verschiedenen Koordinatensysteme müssen wir ineinander umrechnen. Das können wir anschaulich tun – wie hier im Beispiel für Knoten III und Stab 3 und finden
Oder wir wählen einen formalen Ansatz mit der Euer-Transformationsmatrix
,
mit der wir die obige kinematische Beziehung aus
U33 W33 = DR(alpha 3)*U30 W30
gewinnen. Die gesuchten kinematischen Beziehungen erhalten wir für 4 Stäbe an ihren jeweiligen Enden zu
Randbedingungen: die kinematischen Zwangsbedingungen an den Lagern
Zusätzlich zur kinematischen Verträglichkeit müssen wir auch noch die Randbedingungen in Knoten I und II anschrieben:
Randbedingungen: Kräfte und Momente in den Knoten
Es fehlen noch die Gleichgewichtsbedingungen für die Knotenpunkte. Wir erhalten für jeden Knoten – außer denen der Lager – zwei Kraft- und ein Momentengleichgewicht. Für die Lager-Knoten können wir nur die Momentengleichgewichte anschreiben – ohne neue Unbekannte für die Lager-Reaktionskräfte einzufügen.
Die Schnittbilder je Knoten erhalten wir, indem wir die Schnittgrößen an den entsprechenden Schnittufern anzeichnen und dann die Gleichgewichtsbedingungen je Knoten ansetzen.
Auch hier arbeiten wir der Eulerschen Drehmatrix, um diese Arbeit zu formalisieren.
Für Knoten III:
Für Knoten IV:
Für Knoten I und II:
Solving
Wir wählen hier zur Lösung der linearen Gleichungen einen Ansatz, bei dem wir die lokalen Ansatzfunktionen für die Schnittkräfte und die Verschiebungen schon in die Gleichungen der kinematischen Verträglichkeit und des Gleichgewichts einsetzten.
So erhalten wir z.B. aus
die Gleichung
.
Aus der Momentenbilanz für Knoten IV erhalten wir entsprechend
Durch das Einsetzen der Lösungen für uk(xk) und wk(xk) haben wir als Unbekannte nur noch je Stab die 6 Integrationskonstanten Cij, Dij sowie je Knoten die Knotenverschiebungen Koordinaten Uk0, Wk0 und Φk0, also die 36 Unbekannten
X = ….
Für deren Lösung stehen 4 Randbedingungen, 8 Gleichgewichtsbedingungen und 24 kinematische Verträglichkeitsbeziehungen – also 36 Gleichungen - zur Verfügung.
Maxima liefert die Lösungen für unsere 36 Unbekannten. Wir erhalten z.B. für die Normalkraft in Stab 3 den Ausdruck
N3(x3) = …. ,
der für η=0 (die Biegesteifigkeit ist Null)
….
liefert – also die Lösung für das vereinfachte Stabwerk.
Wir tragen für alle Stäbe das Verhältnis Ni/Si auf:
Wenn die Biegesteifigkeit der Stäbe klein wird, konvergiert unsere Lösung gegen die einfache Stabwerkslösung.
Wir vergleichen nun die kritischen Spannungen im Querschnitt der beiden Modelle, also Si/A für das einfache Modell und Ni/A
tmp
Title
Text
1+1
Links
- ...
Literature
- ...