Gelöste Aufgaben/FEC0

Aufgabenstellung

Die schnelle Rotation von Körpern auf Wellen wie z.B. bei Turboladern oder Turbinen führt auf Bewegungsgleichungen, die auch im linearisierten Fall Komponenten der Kreiseldynamik (vgl. GYRO) besitzen.

Rotor in fliegender Lagerung

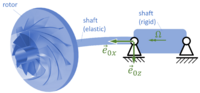
Gesucht sind die Bewegungsgleichungen für einen starren Rotor auf einer masselosen, elastischen Welle. Die Welle dreht sich mit der Drehzahl Ω. Dabei sollen zunächst die linearisierten Bewegungsgleichungen des Systems angeschrieben werden und dessen Eigenwerte für den Idealfall des ausgewuchteten Rotors berechnet werden.

Einige wichtige Systemparameter sind

ℓ	freie Länge des Welle
m	Masse des Rotors
R	max. Rotor-Radius
EI	Biegesteifigkeit der Welle

Lösung mit Maxima

Beim Aufstellen der Bewegungsgleichung von drehenden Körpern geht man oft vom Drall ${\vec {L}}$ (Moment of Momentum), beschreiben als das Skalarprodukt aus Trägheitstensor mal Winkelgeschwindigkeit aus:

${\vec {L}}={\vec {\vec {J}}}\cdot {\vec {\omega }}$.

Dass es - aus meiner Sicht - auch schlanker und intuitiver mit dem Prinzip von d'Alembert geht, zeigen wir hier.

Wir arbeiten mit Maxima.

Maxima brauchen wir dabei zunächst zum Aufstellen der Bewegungsgleichungen, deren Elemente wir dann auf die Komponenten des Drallsatzes zurückführen können. Für den Fall des gewuchteten Rotors (sein Schwerpunkt liegt auf der Rotationsachse und die Deviationsmoments des Trägheitstensors verschwinden) führen wir eine Eigenwertanalyse des Systems für verschiedene Drehzahlen durch - dafür machen wir die Bewegungsgleichungen dimensionslos.

Header

Wir leiten die Bewegungsgleichungen des Systems mit dem Prinzip der virtuellen Verrückungen her. Für die masselose Welle (shaft) ist das einfach, für die Trägheitskräfte des Rotors nutzen wir das Prinzip von d'Alembert, um dessen Tägheitskräfte zu erfassen.

Für die Modalanalyse der linearisierten Bewegungsgleichungen benötigen wir dann etwas mehr, als die Fähigkeiten eines Computer-Algebra-Systems wie Maxima. Hierfür nutzen wir eine bewährte Bibliotheken wie die LaPack - auf die wir aus Maxima heraus zugreifen können.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 22.04.0                           */
/* author: Andreas Baumgart                            */
/* last updated: 2023-10-29                            */
/* ref: Rotor mit fliegender Lagerung                  */
/* description: derives the equations of motion for    */
/*              a rigid roter and elating shaft        */
/*******************************************************/
load (lapack)  $  /* use lapack for numerics           */
fpprintprec : 3$  /* and low number of printed digits  */
/*******************************************************/

Declarations

Wir brauchen zunächst einen Ortsvektor ${\vec {r}}_{P}$ zu einem Massepunkt des Rotors. Dafür nutzen wir die Transformationsmatrizen der Euler-Rotation, also die Drehmatrizen, die unser inertiales Koordinatensystem

${\underline {\vec {e}}}_{0}:=\left({\begin{array}{c}{\vec {e}}_{0x}\\{\vec {e}}_{0y}\\{\vec {e}}_{0z}\end{array}}\right)$

in das Wellen-feste Koordinatensystem ${\underline {\vec {e}}}_{s}$ durch eine Drehung um Ω t bzgl. der "x"- oder "1"-Achse überführt:

${\underline {\vec {e}}}_{S}:={\underline {\underline {D}}}_{1}(\Omega \;t)\cdot {\underline {\vec {e}}}_{0}$.

Koordinaten des Welle-Rotor-Koppelpunktes V(t) und W(t).

Der Ortsvektor des Koppelpunktes von Rotor und Welle ist dann in unserem inertialen Koordinatensystem

${\vec {r}}_{P,0}=\left(\ell ,V(t),W(t)\right)\cdot {\underline {\vec {e}}}_{S}$

mit den Koordinaten des Durchstoßpunktes V(t) und W(t) und der freien Länge der Welle ℓ. Von ${\vec {r}}_{P,0}$ kommen wir zu einem beliebigen Punkt $(x,y,z)$ auf dem Rotor mit dem Rotor-festen Koordinatensystems

${\underline {\vec {e}}}_{R}:={\underline {\underline {D}}}_{2}(-\Phi (t))\cdot {\underline {\underline {D}}}_{3}(\Psi (t))\cdot {\underline {\underline {D}}}_{1}(\Omega \;t)\cdot {\underline {\vec {e}}}_{0}$,

in das die Kippwinkel Ψ(t) bzgl. der "z"-Achse und Φ(t) bzgl. der "y"-Achse eingehen. Damit ist

${\vec {r}}_{P}:={\vec {r}}_{P,0}+\left(x,y,z)\right)\cdot {\underline {\vec {e}}}_{R}$.

Koordinaten des Rotor-Auslenkung und Kippung W(t), Φ(t)

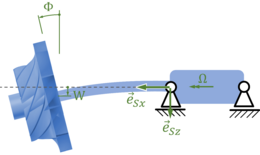
Wir drehen hier bzgl. der y-Achse um -Φ(t), damit wir die Beziehungen der klassischen Euler-Bernoulli-Biegetheorie (hier: $w'(\ell )=\Phi$) nutzen können. Die Koordinaten des Rotors sind damit

${\underline {Q}}:=\left({\begin{array}{c}V(t)\\\Psi (t)\\W(t)\\\Phi (t)\end{array}}\right)$.

Da wir uns nur für die linearisierte Form der Bewegungsgleichungen des starren Rotors interessieren, können wir gleich die linearisierten Drehmatrizen ${\underline {\underline {D}}}_{L,i}(.)$ in Maxima nutzen.

/* Declarations      */
/* Euler - Rotations */
D[1](φ) := matrix([1,0,0],[0,cos(φ),+sin(φ)],[0,-sin(φ),cos(φ)]);
D[2](φ) := matrix([cos(φ),0,-sin(φ)],[0,1,0],[+sin(φ),0,cos(φ)]);
D[3](φ) := matrix([cos(φ),+sin(φ),0],[-sin(φ),cos(φ),0],[0,0,1]);
/* ... linearized */
DL[2](φ) := matrix([1,0,-φ],[0,1,0],[+φ,0,1]);
DL[3](φ) := matrix([1,φ,0],[-φ,1,0],[0,0,1]);

/* trigonometric replacements */
trigReplace : [sin(Ω*t)^2=1-cos(Ω*t)^2, cos(Ω*t)^2=(cos(2*Ω*t)+1)/2, cos(Ω*t)=sin(2*Ω*t)/sin(Ω*t)/2];

/* minimal coordinates of motion */
Q: [[ V(t),  Ψ(t),  W(t),  Φ(t)], 
    [δV   , δΨ   , δW   , δΦ   ]];
/* variation of coordinates            */
varia: makelist(Q[1][i]=Q[2][i],i,1,4);
/* null-reference for linearization   */
nuller : makelist(Q[1][i]=0,i,1,4);

Equations of Motion

Bei der Herleitung der Bewegungsgleichungen aus dem Prinzip der virtuellen Verrückungen benötigen wir für die Gleichgewichtsbedingungen

${\begin{array}{ll}\delta W&=\delta W^{a}-\delta \Pi \\&{\stackrel {!}{=}}0\end{array}}$.

die virtuelle Arbeit der d'Alembertschen Trägeheitskräfte $\delta W^{a}$ und die virtuelle Formänderungsenergie $\delta \Pi$.

Dabei kommt

$\delta W^{a}=\int _{m}-\delta {\vec {r}}\cdot {\vec {\ddot {r}}}_{P}(t)\;dm$

aus dem Integral über alle Massepunkte des Rotors. Wir finden durch Vereinfachen und Umsortieren

$\delta W^{a}=-\delta Q^{T}\cdot \int _{m}{\underline {\underline {\tilde {M}}}}\;{\underline {\ddot {Q}}}+{\underline {\underline {\tilde {G}}}}\;{\underline {\dot {Q}}}+{\underline {\underline {\tilde {E}}}}\;{\underline {Q}}-{\underline {\tilde {B}}}(t)\;dm$.

So steht jetzt z.B. in der Massenmatrix

${\underline {\underline {\tilde {M}}}}={\begin{pmatrix}1&x&0&0\\x&{{y}^{2}}+{{x}^{2}}&0&yz\\0&0&1&x\\0&yz&x&{{z}^{2}}+{{x}^{2}}\end{pmatrix}}$,

über deren Elemente wir die Integration über die Masse m ausführen müssen. Hier greifen jetzt die Definitionen für den Schwerpunkt eines Körper (z.B. $Y_{S}$) und für die Massemeomente 2-ten Grades, so dass wir mit folgenden Abkürzungen arbeiten können

${\begin{array}{lcll}\int _{m}&1&dm=&\;\;\;\;m\\\int _{m}&y^{2}+z^{2}&dm=&+J_{xx}\\\int _{m}&x^{2}+z^{2}&dm=&+J_{yy}\\\int _{m}&x^{2}+y^{2}&dm=&+J_{zz}\\\int _{m}&x\;y&dm=&-J_{xy}\\\int _{m}&y\;z&dm=&-J_{yz}\\\int _{m}&x\;z&dm=&-J_{xz}\\\int _{m}&x^{2}&dm=&\;\;\;\;\Theta ={\frac {1}{2}}\left(J_{yy}+J_{zz}-J_{xx}\right)\\\int _{m}&x&dm=&\;\;\;\;X_{S}\;m\\\int _{m}&y&dm=&\;\;\;\;Y_{S}\;m\\\int _{m}&z&dm=&\;\;\;\;Z_{S}\;m\\\end{array}}$

Für die virtuelle Formänderungsenergie setzen wir mit den tabellierten Lösungen für den Kragballken und dem Blaken unter Endmoment bei einer Biegung um die y-Achse

$\delta \Pi _{y}=\delta \Phi \;\left({\frac {\displaystyle 4EI}{\ell }}\;\Phi (t)-{\frac {\displaystyle 6EI}{\ell ^{2}}}\;W(t)\right)+\delta W\;\left({\frac {\displaystyle 12EI}{\ell ^{3}}}\;W(t)-{\frac {\displaystyle 6EI}{\ell ^{2}}}\;\Phi (t)\right)$

an. Die gleichen Anteile finden wir natürlich dann bzgl. der Biegung um die z-Achse.

Einsetzen in die Gleichgewichtsbeziehungen liefert den Ausdruck

${\underline {\underline {M}}}\;{\underline {\ddot {Q}}}+{\underline {\underline {G}}}\;{\underline {\dot {Q}}}+{\underline {\underline {E}}}\;{\underline {Q}}+{\underline {\underline {K}}}\;{\underline {Q}}={\underline {B}}(t)$

mit

${\underline {\underline {M}}}=\;\;\;{\begin{pmatrix}m&{X_{S}}m&0&0\\{X_{S}}m&J_{zz}&0&-J_{yz}\\0&0&m&{X_{S}}m\\0&-J_{yz}&{X_{S}}m&J_{yy}\end{pmatrix}}$

${\underline {\underline {G}}}=2\Omega {\begin{pmatrix}0&0&-m&-{X_{S}}m\\0&0&-{X_{S}}m&-\Theta \\m&{X_{S}}m&0&0\\{X_{S}}m&\Theta &0&0\end{pmatrix}}$

${\underline {\underline {E}}}=\;\Omega ^{2}{\begin{pmatrix}-m&-{X_{S}}m&0&0\\-{X_{S}}m&-\Theta m&0&0\\0&0&-m&-{X_{S}}m\\0&0&-{X_{S}}m&-\Theta \end{pmatrix}}$

${\underline {\underline {K}}}=\;\;\;{\begin{pmatrix}{\frac {12EI}{\ell ^{3}}}&-{\frac {6EI}{\ell ^{2}}}&0&0\\-{\frac {6EI}{\ell ^{2}}}&{\frac {4EI}{\ell }}&0&0\\0&0&{\frac {12EI}{\ell ^{3}}}&-{\frac {6EI}{\ell ^{2}}}\\0&0&-{\frac {6EI}{\ell ^{2}}}&{\frac {4EI}{\ell }}\end{pmatrix}}$

${\underline {B}}={\begin{pmatrix}{Y_{S}}m{{\Omega }^{2}}\\-J_{xy}{{\Omega }^{2}}\\{Z_{S}}m{{\Omega }^{2}}\\-J_{xz}{{\Omega }^{2}}\end{pmatrix}}$

Die Koeffizienten Θ nehmen hier eine Sonderstellung ein - sie stehen für die Entwicklung von Zentrifugalkräften aus der elastischen Verformung der Welle.

/*******************************************************/
/******************* PART   I **************************/
/*******************************************************/
/* compute elements of virtual work for rotor and shaft*/

/***********************************/
/* matrices from d'Alembert forces for Rotor */
r : expand(matrix([0,V(t),W(t)]).D[1](  Ω*t )
          +matrix([x,  y ,  z ]).DL[2](-Φ(t)).DL[3](Ψ(t)).D[1](Ω*t))$
/* linearize*/
r : subst(nuller,r) + sum(subst(nuller,diff(r,Q[1][j]))*Q[1][j],j,1,4)$
/* Variation of ...*/
δr : sum(subst(nuller,diff(r,Q[1][j]))*Q[2][j],j,1,4)$
/***************************************/
/* equilibrium conditions with the PvV */

/* virtual work of d'Alembert forces   */
δWa: expand(trigsimp(expand(-δr.diff(r,t,2))));

/* subtract all contributinos of identified coefficients from virtual work */
rest : δWa$

M : -funmake('matrix,makelist(coeff(makelist(coeff(rest,diff(Q[1][i],t,2)),i,1,4),Q[2][j]),j,1,4));
rest: expand(rest + Q[2].M.transpose(diff(Q[1],t,2)));

G : -funmake('matrix,makelist(coeff(makelist(coeff(rest,diff(Q[1][i],t,1)),i,1,4),Q[2][j]),j,1,4))/(2*Ω);
rest: expand(rest + Q[2].G.transpose(diff(Q[1],t,1))*(2*Ω));

E : -funmake('matrix,makelist(coeff(makelist(coeff(rest,diff(Q[1][i],t,0)),i,1,4),Q[2][j]),j,1,4))/Ω^2;
rest: expand(rest + Q[2].E.transpose(diff(Q[1],t,0))*(Ω^2));

B : +transpose(makelist(coeff(rest,Q[2][i]),i,1,4));

/* choose appropriate abbreviations for results of integration over rotor mass */
intdm : [1 = m, y^2+x^2 = J[zz], z^2+x^2 = J[yy], x*y = -J[xy], y*z = -J[yz], x*z = -J[xz], x^2 = Θ, x = X[S]*m, y = Y[S]*m, z = Z[S]*m];
M: subst(intdm, M);
G: subst(intdm, G);
E: subst(intdm, E);
B: Ω^2*subst(intdm, B/Ω^2);

/******************************************/
/* matrices from strain energy for Shaft */
/* e.g. from Gross e.a. */
table: [EI*W(t)=f[0]*ℓ^3/3+m[0]*ℓ^2/2,EI*Φ(t)=f[0]*ℓ^2/2+m[0]*ℓ];
table: solve(table,[f[0],m[0]])[1];

/* virtual strain energy                 */
δΠ: expand(subst(table,f[0]*δW+m[0]*δΦ));
Ke: makelist(coeff(makelist(coeff(δΠ,Q[2][i]),i,3,4),Q[1][j]),j,3,4);
K : zeromatrix(4,4);
for i:1 thru 2 do
    for j:1 thru 2 do
        (K[  i,  j] : K[  i,  j] + Ke[i][j],
         K[2+i,2+j] : K[2+i,2+j] + Ke[i][j]);

/********************************************/
print(M,"*","Q''","+",(2*Ω),"*",G,"*","Q'","+",Ω^2,"*",E, "Q","+",K, "*","Q"," = ",B)$

Rewrite as Dimensionless Equations of Motion

Für die Modalanalyse können wir die Anzahl der Systemparameter reduzieren, indem wir die Bewegungsgleichungen auf eine dimensionslose Schreibweise umstellen. Dafür ersetzen wir Koordinaten und Größen in den Bewegungsgleichung nach dieser Vorlage:

${\begin{array}{lll}t&=&\tau /\omega _{0}\\\omega _{0}^{2}&=&k/m\\\Omega &=&\lambda \;\omega _{0}\\k&=&{\frac {\displaystyle 12EI}{\displaystyle \ell ^{3}}}\\\ell &=&\kappa \;R\\V(t)&=&R\;v(\tau )\\W(t)&=&R\;w(\tau )\\\Psi (t)&=&\;\;\;\;\psi (\tau )\\\Phi (t)&=&\;\;\;\;\phi (\tau )\\X_{S}&=&R\;\xi _{S}\\Y_{S}&=&R\;\eta _{S}\\Z_{S}&=&R\;\zeta _{S}\\J_{yy}&=&\left(R\;\rho _{yy}\right)^{2}\;m\\J_{zz}&=&\left(R\;\rho _{zz}\right)^{2}\;m\\J_{xy}&=&\left(R\;\rho _{xy}\right)^{2}\;m\\J_{xz}&=&\left(R\;\rho _{xz}\right)^{2}\;m\\\Theta &=&\left(R\;\rho _{xx}\right)^{2}\;m\;(!)\end{array}}$

Dabei ist $\rho _{ij}$ der jeweilige dimensionslose Trägheitsradius des Rotors. Der Trägheitsradius ist ein Äquivalenzwert, der dabei hilft, unbekannte Systemparameter - wie die Massenmomente - abzuschätzen. Am Beispiel von $J_{xz}$ soll dies

X

Y

Mit diesen neuen Größen und Abkürzungen können wir unsere Bewegungsgleichungen durch "$\omega _{0}^{2}Rm$" für die Zeilen von $\delta V,\delta W$ und "$\omega _{0}^{2}R^{2}m$" für die Zeilen von $\delta \Psi ,\delta \Phi$ teilen und erhalten mit

${\underline {q}}:=\left({\begin{array}{c}v(\tau )\\\psi (\tau )\\w(\tau )\\\phi (\tau )\end{array}}\right)$

die Bewegungsgleichungen

${\underline {\underline {M}}}\;{\underline {q''}}+{\underline {\underline {G}}}\;{\underline {q'}}+\left({\underline {\underline {E}}}+{\underline {\underline {K}}}\right)\;{\underline {q}}={\underline {B}}$

mit

${\frac {\displaystyle d}{d\tau }}(q)=:q'$

sowie den neuen Systemmatrizen

${\underline {\underline {M}}}=\;\;\;{\begin{pmatrix}1&{{\xi }_{S}}&0&0\\{{\xi }_{S}}&{{\rho }_{zz}^{2}}&0&-{{\rho }_{yz}^{2}}\\0&0&1&{{\xi }_{S}}\\0&-{{\rho }_{yz}^{2}}&{{\xi }_{S}}&{{\rho }_{yy}^{2}}\end{pmatrix}}$

${\underline {\underline {G}}}=2\;\lambda \;{\begin{pmatrix}0&0&-1&-{{\xi }_{S}}\\0&0&-{{\xi }_{S}}&-{{\rho }_{xx}^{2}}\\1&{{\xi }_{S}}&0&0\\{{\xi }_{S}}&{{\rho }_{xx}^{2}}&0&0\end{pmatrix}}$

${\underline {\underline {E}}}=\;\lambda ^{2}\;{\begin{pmatrix}-1&-{{\xi }_{S}}&0&0\\-\xi _{S}&-\rho _{xx}^{2}&0&0\\0&0&-1&-\xi _{S}\\0&0&-{{\xi }_{S}}&-{{\rho }_{xx}^{2}}\end{pmatrix}}$

${\underline {\underline {K}}}=\;\;\;{\begin{pmatrix}1&-{\frac {\kappa }{2}}&0&0\\-{\frac {\kappa }{2}}&{\frac {{\kappa }^{2}}{3}}&0&0\\0&0&1&-{\frac {\kappa }{2}}\\0&0&-{\frac {\kappa }{2}}&{\frac {{\kappa }^{2}}{3}}\end{pmatrix}}$

${\underline {\underline {B}}}=\;\lambda ^{2}\;{\begin{pmatrix}{{\eta }_{S}}\\-{{\rho }_{xy}^{2}}\\{{\zeta }_{S}}\\-{{\rho }_{xz}^{2}}\end{pmatrix}}$

/*******************************************************/
/******************* PART  II **************************/
/*******************************************************/
/* transfer to dimensionless representation            */

dimless: [[EI = k*ℓ^3/12, X[S]=ξ[S]*R, Y[S]=η[S]*R, Z[S]=ζ[S]*R,
           Ω = λ*ω[0], k = m*ω[0]^2, ℓ=κ*R,
           Θ = m*(R*ρ[xx])^2, /* Warschau! deviates from other abbreviations */
	   J[zz] = m*(R*ρ[zz])^2, J[yy] = m*(R*ρ[yy])^2, J[xy] = m*(R*ρ[xy])^2, J[yz] = m*(R*ρ[yz])^2, J[xz] = m*(R*ρ[xz])^2],
	  [t = τ/ω[0], ω[0]^2 = (12*EI)/ℓ^3/m, W(t)=w(τ)*R, V(t)=v(τ)*R, Ψ(t)=ψ(τ), Φ(t)=φ(τ)]];

applyTo: [M,G,E,K];
for a: 1 thru 4 do
(for i:1 thru 4 step 2 do
   (applyTo[a][i]: applyTo[a][i]*R, /* for δW and δV*/
    for j:1 thru 4 step 1 do
       applyTo[a][j][i]: applyTo[a][j][i]*R)); /* for W and V*/
       
for i:1 thru 4 step 2 do
    B[i]:B[i]*R;

M:     M*ω[0]^2;
G: 2*Ω*G*ω[0]  ;
E: Ω^2*E       ;


print(M,"*","Q''","+",G,"*","Q'","+",E, "Q","+",K, "*","Q"," = ",B)$

/* devide through common factots .... */
M: subst(dimless[1],M/(ω[0]^2*R^2*m));
G: subst(dimless[1],G/(ω[0]^2*R^2*m));
E: subst(dimless[1],E/(ω[0]^2*R^2*m));
K: subst(dimless[1],K/(ω[0]^2*R^2*m));
B: subst(dimless[1],B/(ω[0]^2*R^2*m));

/* dimless model */
print(M,"*","Q''","+",G,"*","Q'","+",E, "Q","+",K, "*","Q"," = ",B)$

paramList: [λ,κ,
            ξ[S],η[S],ζ[S],
            ρ[xx], ρ[yy], ρ[zz], ρ[xy], ρ[yz], ρ[xz]];

Solving

Wir interessieren uns bei einer Modalanalyse nur für Lösungen ohne Zwangserregung ${\underline {B}}$, also für $\eta _{S}=0$, $\zeta _{S}=0$, $\rho _{xy}=0$ und $\rho _{xz}=0$.

Mit dem Ansatz

${\underline {q}}(\tau )={\underline {\hat {q}}}\cdot e^{\Lambda \;\tau }$

suchen wir also nach Lösungen von

$\Lambda ^{2}\cdot {\underline {\underline {M}}}+\Lambda \cdot {\underline {\underline {G}}}+\left({\underline {\underline {E}}}+{\underline {\underline {K}}}\right)={\underline {0}}$

Für numerische Löser muss das Problem allerdings fast immer als

$\Lambda \;{\underline {\underline {B}}}+{\underline {\underline {A}}}={\underline {0}}$

formuliert sein. Wir schaffen die Anbindung mit dem Trick

${\underline {r}}=\left({\begin{array}{c}q\\p\end{array}}\right){\mbox{ und }}p=q'$

Dann ist

${\underline {\underline {B}}}=\left({\begin{array}{cc}{\underline {\underline {M}}}&{\underline {\underline {0}}}\\{\underline {\underline {0}}}&{\underline {\underline {1}}}\\\end{array}}\right)$

und

${\underline {\underline {A}}}=\left({\begin{array}{cc}{\underline {\underline {G}}}&{\underline {\underline {E}}}+{\underline {\underline {K}}}\\-{\underline {\underline {1}}}&{\underline {\underline {0}}}\\\end{array}}\right)$

Für die restlichen dimensionslosen Parameter in den Matrizen wählen wir nun geschätzte Werte - eine Berechnung der wirklichen Werte würde man wohl eher einem CAD oder FEM-Programm überlassen ....

${\begin{array}{lll}\kappa &=&0.2\\\xi _{S}&=&0.1\\\rho _{xx}&=&0.15{\mbox{ Achtung: es muss gelten }}\rho _{xx}>\xi _{S}\\\rho _{yy}&=&\rho _{zz}{\mbox{ (Rotationssymmetrie!)}}\\\rho _{zz}&=&0.2\\\end{array}}$

/*******************************************************/
/******************* PART III **************************/
/*******************************************************/
/* rewrite as first-order differential equations       */
/* and solve using lapack https://www.netlib.org/lapack/explore-html/d9/d8e/group__double_g_eeigen_ga66e19253344358f5dee1e60502b9e96f.html */

params: [/*λ = 2,*/
         κ = 2,
         ξ[S]=0.1,η[S]=0,ζ[S]=0,
         ρ[xx]=0.15, ρ[yy]=ρ[zz], ρ[zz]=0.2, ρ[xy]=0, ρ[yz]=0, ρ[xz]=0];

A: zeromatrix(8,8);
B: zeromatrix(8,8);
for i:1 thru 4 do 
   (B[4+i,4+i]: +1,
    A[4+i,  i]: -1,
    for j:1 thru 4 do 
       (A[  i,  j]: G[i,j],
        A[  i,4+j]: E[i,j]+K[i,j],
        B[  i,  j]: M[i,j]))$

collect : [[],[]];
for lambda:0 thru 12 step 0.03 do
   (C: invert(subst([λ = lambda],subst(params,B))).subst([λ = lambda],subst(params,A)),
    evs: [args(dgeev (C)[1])],
    collect[1]: append(collect[1], [lambda]),
    collect[2]: append(collect[2], evs));

Postprocessing

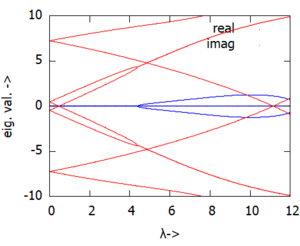
Die Auftragung der Eigenwerte über der Drehzahl λ zeigt nun für λ > 4.5 auch instabile Lösungen - also Bewegungen mit exponentiellem Wachstum der Amplituden der Lösungen.

Dimensionslose Eigenwerte (Real- und Imaginärteil) aufgetragen über die dimensionslose Drehzahl λ.

Und jetzt?

... wäre es natürlich spannend, sich die Eigenformen zu den Eigenwerten anzuschauen - insbesondere für die Eigenwerte, bei denen $Re(\Lambda )>0$ ist.

xyr: [];
xyi: [];
for e:1 thru length(collect[1]) do
   (xyr: append(xyr, makelist([collect[1][e],realpart(collect[2][e][i])],i,1,8)),
    xyi: append(xyi, makelist([collect[1][e],imagpart(collect[2][e][i])],i,1,8)));

/* plot eigenvalues */
plot2d([[discrete, xyr],[discrete, xyi]], [legend,"real","imag"],[style, [points,0.1,1,1], [points,0.1,2,1]],
       [y,-10,10],  
       [xlabel,"λ->"], [ylabel,"eig. val. ->"])$

---

Links

• FEAC1
• GYRO

Literature

• ...