Gelöste Aufgaben/FEC0

Aufgabenstellung

Die schnelle Rotation von Körpern auf Wellen wie z.B. bei Turboladern oder Turbinen führt auf Bewegungsgleichungen, die auch im linearisierten Fall Komponenten der Kreiseldynamik (vgl. GYRO) besitzen.

Rotor in fliegender Lagerung

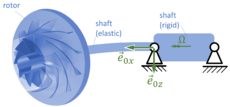
Gesucht sind die Bewegungsgleichungen für einen starren Rotor auf einer masselosen, elastischen Welle. Die Welle dreht sich mit der Drehzahl Ω. Dabei sollen zunächst die linearisierten Bewegungsgleichungen des Systems angeschrieben werden und dessen Eigenwerte für den Idealfall des ausgewuchteten Rotors berechnet werden.

Lösung mit Maxima

Beim Aufstellen der Bewegungsgleichung von drehenden Körpern geht man oft vom Drall ${\vec {L}}$ (Moment of Momentum), beschreiben als das Skalarprodukt aus Trägheitstensor mal Winkelgeschwindigkeit aus:

${\vec {L}}={\vec {\vec {J}}}\cdot {\vec {\omega }}$.

Dass es - aus meiner Sicht - auch schlanker und intuitiver mit dem Prinzip von d'Alembert geht, zeigen wir hier.

Wir arbeiten mit Maxima.

Maxima brauchen wir dabei zunächst zum Aufstellen der Bewegungsgleichungen, deren Elemente wir dann auf die Komponenten des Drallsatzes zurückführen können. Für den Fall des gewuchteten Rotors (sein Schwerpunkt liegt auf der Rotationsachse und die Deviationsmoments des Trägheitstensors verschwinden) führen wir eine Eigenwertanalyse des Systems für verschiedene Drehzahlen durch - dafür machen die Bewegungsgleichungen dimensionslos.

Header

Wir leiten die Bewegungsgleichungen des Systems mit dem Prinzip der virtuellen Verrückungen her. Für die masselose Welle (shaft) ist das einfach, für die Trägheitskräfte des Rotors nutzen wir das Prinzip von d'Alembert, um dessen Tägheitskräfte zu erfassen.

Für die Modalanalyse der linearisierten Bewegungsgleichungen benötigen wir dann etwas mehr, als die Fähigkeiten eines Computer-Algebra-Systems wie Maxima. Hierfür nutzen wir eine bewährte Bibliotheken wie die LaPack - auf die aus Maxima heraus zugreifen können.

/*******************************************************/
/* MAXIMA script                                       */
/* version: wxMaxima 22.04.0                           */
/* author: Andreas Baumgart                            */
/* last updated: 2023-10-29                            */
/* ref: Rotor mit fliegender Lagerung                  */
/* description: derives the equations of motion for    */
/*              a rigid roter and elating shaft        */
/*******************************************************/
load (lapack)  $  /* use lapack for numerics           */
fpprintprec : 3$  /* and low number of printed digits  */
/*******************************************************/

Declarations

Wir brauchen zunächst einen Ortsvektor ${\vec {r}}_{P}$ zu einem Massepunkt des Rotors. Dafür nutzen wir die Transformationsmatrizen der Euler-Rotation, also die Drehmatrizen, die unser inertiales Koordinatensystem

${\underline {\vec {e}}}_{0}:={\begin{array}{c}{\vec {e}}_{0x}\\{\vec {e}}_{0y}\\{\vec {e}}_{0z}\end{array}}$

in das Wellen-feste Koordinatensystem ${\underline {\vec {e}}}_{0}$ überführt. Wir kippen zunächst um die x₂-Achse, dann um die resultierende x'₁-Achse und schließlich um die Rotationsachse x"₃. Die Koordinatentransformation ist dann

${\underline {\underline {D}}}_{0\to K}={\underline {\underline {D}}}_{3}(\varphi _{3}(t))\cdot {\underline {\underline {D}}}_{1}(\varphi _{1}(t))\cdot {\underline {\underline {D}}}_{2}(\varphi _{2}(t))$.

1+1

Geomertrie des Kreisels

Geomertrie des Kreisels

Für unser System brauchen wir einen Ansatz, der diese Transformation - und weitere - formalisiert (→ Drehmatrix).

Equations of Motion

Text

1+1

Solving

Text

1+1

Postprocessing

Text

1+1

---

Links

• FEAC1
• GYRO

Literature

• ...