Sources/Lexikon/Axiome der Statik: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung |
||
| Zeile 3: | Zeile 3: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
!style="text-align:left"| | !style="text-align:left"|Gleichgewicht für zwei Kräfte am starren Körper | ||
|- | |- | ||
| | | | ||
=== Axiom 1: === | |||
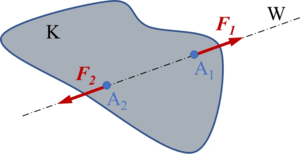
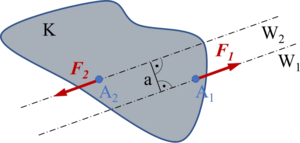
Ein freier, starrer Körper Κ ist unter der Wirkung von zwei Kräften ''F<sub>1</sub>, F<sub>2</sub>'' dann und nur dann im Gleichgewicht, wenn sie in die Verbindungslinie ihrer beiden Angriffspunkte ''A<sub>1</sub>'', ''A<sub>2</sub>'' fallen, entgegengesetzt orientiert und gleich groß sind. | Ein freier, starrer Körper Κ ist unter der Wirkung von zwei Kräften ''F<sub>1</sub>, F<sub>2</sub>'' dann und nur dann im Gleichgewicht, wenn sie in die Verbindungslinie ihrer beiden Angriffspunkte ''A<sub>1</sub>'', ''A<sub>2</sub>'' fallen, entgegengesetzt orientiert und gleich groß sind. | ||
{| class="wikitable" | {| class="wikitable" | ||
| Zeile 23: | Zeile 22: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
! style="text-align:left" | | ! style="text-align:left" |Kräfte-Parallelogramm | ||
|- | |- | ||
| | | | ||
===Axiom 2:=== | |||
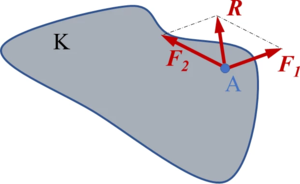
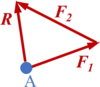
Greifen zwei Kräfte F1 und F2 an einem gemeinsamen Angriffspunkt A an, so können sie durch eine Kraft R ersetzt werden, die sich als die Diagonale des durch die beiden Kräfte aufgespannten Parallelogramms ergibt, Bild 3. | Greifen zwei Kräfte F1 und F2 an einem gemeinsamen Angriffspunkt A an, so können sie durch eine Kraft R ersetzt werden, die sich als die Diagonale des durch die beiden Kräfte aufgespannten Parallelogramms ergibt, Bild 3. | ||
Gemäß Bild 3, ist die Diagonale R die (geometrische) Summe der beiden Vektoren F1 und F2 : | Gemäß Bild 3, ist die Diagonale R die (geometrische) Summe der beiden Vektoren F1 und F2 : | ||
| Zeile 57: | Zeile 54: | ||
{| class="wikitable" | {| class="wikitable" | ||
|+ | |+ | ||
!style="text-align:left"| | !style="text-align:left"|Hinzufügen oder Wegnehmen einer Gleichgewichtsgruppe | ||
|- | |- | ||
| | |'''Definition''': Eine Gruppe von zwei oder mehr Kräften, die sich - allein auf einen freien, starren Körper Κ wirkend - im Gleichgewicht hält, heißt Gleichgewichtsgruppe. | ||
Beispiel: Die beiden Kräfte aus Axiom 1. | |||
=== Axiom 3: === | |||
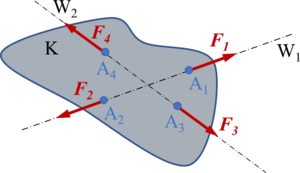
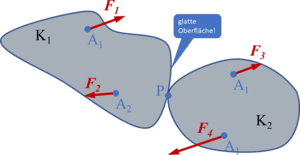
Befindet sich ein freier, starrer Körper Κ (unter der Wirkung von irgendwelchen Kräften) im Gleichgewicht, so bleibt er im Gleichgewicht, wenn eine Gleichgewichtsgruppe | Befindet sich ein freier, starrer Körper Κ (unter der Wirkung von irgendwelchen Kräften) im Gleichgewicht, so bleibt er im Gleichgewicht, wenn eine Gleichgewichtsgruppe | ||
hinzugefügt oder weggenommen wird. In dem als Beispiel skizzierten System von Bild A3-1 sei der Körper Κ unter der Wirkung der Kräfte <math display="inline">\vec{F}_1</math>, <math display="inline">\vec{F}_2</math> im Gleichgewicht (vgl. Axiom 1). Die hinzugefügte Gleichgewichtsgruppe <math display="inline">\vec{F}_3</math>, <math display="inline">\vec{F}_4</math> die ihrerseits Axiom 1 genügt, ändert den Gleichgewichtszustand des Körpers Κ nicht! | hinzugefügt oder weggenommen wird. In dem als Beispiel skizzierten System von Bild A3-1 sei der Körper Κ unter der Wirkung der Kräfte <math display="inline">\vec{F}_1</math>, <math display="inline">\vec{F}_2</math> im Gleichgewicht (vgl. Axiom 1). Die hinzugefügte Gleichgewichtsgruppe <math display="inline">\vec{F}_3</math>, <math display="inline">\vec{F}_4</math> die ihrerseits Axiom 1 genügt, ändert den Gleichgewichtszustand des Körpers Κ nicht! | ||
Version vom 17. Februar 2021, 14:09 Uhr
| Kräfte-Parallelogramm | |||||||||
|---|---|---|---|---|---|---|---|---|---|
Axiom 2:Greifen zwei Kräfte F1 und F2 an einem gemeinsamen Angriffspunkt A an, so können sie durch eine Kraft R ersetzt werden, die sich als die Diagonale des durch die beiden Kräfte aufgespannten Parallelogramms ergibt, Bild 3. Gemäß Bild 3, ist die Diagonale R die (geometrische) Summe der beiden Vektoren F1 und F2 :
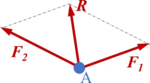
Das Kräfteparallelogramm (Bild 3) enthält den Angriffspunkt A, im Kräftedreieck (Krafteck, Kräfteplan) bleibt der Angriffspunkt unberücksichtigt (vgl. Bild).
Definition: Gemäß dem Kräfteparallelogramm in Bild führt man als resultierende Kraft - kurz Resultierende - der beiden (Einzel-)Kräfte und ein. Die Resultierende ersetzt die (Wirkung der) Einzelkräfte!
|
| Hinzufügen oder Wegnehmen einer Gleichgewichtsgruppe | ||
|---|---|---|
| Definition: Eine Gruppe von zwei oder mehr Kräften, die sich - allein auf einen freien, starren Körper Κ wirkend - im Gleichgewicht hält, heißt Gleichgewichtsgruppe.
Beispiel: Die beiden Kräfte aus Axiom 1. Axiom 3:Befindet sich ein freier, starrer Körper Κ (unter der Wirkung von irgendwelchen Kräften) im Gleichgewicht, so bleibt er im Gleichgewicht, wenn eine Gleichgewichtsgruppe hinzugefügt oder weggenommen wird. In dem als Beispiel skizzierten System von Bild A3-1 sei der Körper Κ unter der Wirkung der Kräfte , im Gleichgewicht (vgl. Axiom 1). Die hinzugefügte Gleichgewichtsgruppe , die ihrerseits Axiom 1 genügt, ändert den Gleichgewichtszustand des Körpers Κ nicht!
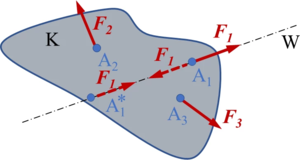
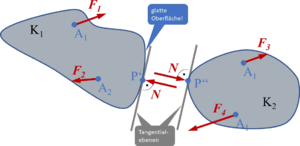
So sei der in Bild A3-2 gezeigte Körper unter der Wirkung der Kräfte , , im Gleichgewicht. Wir legen die Gleichgewichtsgruppe , (in Bild A3-2 gestrichelt) so auf den Körper, dass , bei A1 und im Punkt A* angreift. Dann heben sich die bei A1 angreifenden Kräfte auf (ihre Resultierende verschwindet), wir erhalten die „längs der Wirkungslinie W nach A1 verschobene Kraft ." |

x x x x x x x x x