Sources/Lexikon/Kontaktkennlinie: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 65: | Zeile 65: | ||
[[Datei:Kontaktkennlinie-15.png|mini|Kennlinie mit dynamischem Verlustglied. Schraffiert ist die Verlustarbeit beim einem Schwingungszyklus]] | [[Datei:Kontaktkennlinie-15.png|mini|Kennlinie mit dynamischem Verlustglied. Schraffiert ist die Verlustarbeit beim einem Schwingungszyklus]] | ||
Dafür multiplizieren wir den Ausdruck für die Kraft <i>F</i> mit dem Geschwindigkeitsabhängigen Verlustglied <i>l(v)</i> mit | Dafür multiplizieren wir den Ausdruck für die Kraft <i>F</i> mit dem Geschwindigkeitsabhängigen Verlustglied <i>l(v)</i> - z.B. mit | ||
::<math>l(v) = \left{\begin{array}{l}1\\2\\3\end{array} \right. \text{ und } v = \frac{\displaystyle dh}{\displaystyle dt} </math>. | ::<math>l(v) = \left\{\begin{array}{l}1\\2\\3\end{array} \right. \text{ und } v = \frac{\displaystyle dh}{\displaystyle dt} </math>. | ||
Version vom 31. Mai 2022, 10:37 Uhr
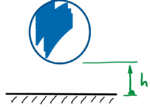
Beim Billard prallen zwei Körper aufeinander und trennen sich dann wieder. Der Löser der Bewegungsgleichungen braucht also eine Kraft, die "da" ist, wenn der Abstand der Kugelmittelpunkte kleiner als der Kugeldurchmesser ist - und Null sonst.
Für die Bewegungsgleichung eines solchen Systems müssen wir die Kraft erfassen, die im Kontakt zwischen zwei Körpern wirkt. Ein Finite Elemente Modell könnte diese Kraft als Resultierende der Kontakt-Drücke für verschiedene Eindringtiefen ermitteln.
 |
 |
Das ist ist aufwändig und teuer.
Einfacher kommen wir mit einer Kontaktkennlinie zum Ziel, die ein heuristisches Modell der Kontaktkraft ist.
Stückweise linearer Ansatz
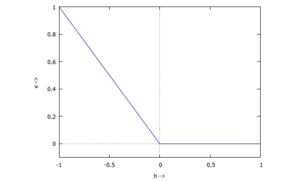
Wir suchen also eine Funktion, die für h<0 einen positive Wert (Druck) zurückliefert und Null sonst. Als Kontaktkraft schreiben wir
mit der Federkonstante k und der nichtlinearen Funktion κ(h).
κ(h) wählen wir zu:
Maxima-Code
Zum Einbauen in Ihr Programm: der Quellcode zur Kennlinie.
/* contact characteristic */
kappa(h) := if h>0 then 0 else -h;
plot2d(kappa(h),[h,-1,1], [y,-0.1,1], [xlabel, "h/ε->"], [ylabel, "κ ->"])$
Ausrunden der Kennlinie
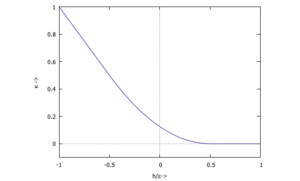
... hier für ε=0.5
Damit die Kennlinie stetig differenzierbar ist, brauchen wir ein "Ausrundungspolynom" um h=0 herum.
Für -ε < h < ε wählen wir ein Polynom 2.ten Graden und passen es stetig an die beiden Geradenstücke an.
Dann ist die nichtlineare Funktion κ(h,ε):
Maxima-Code
Zum Einbauen in Ihr Programm: der Quellcode zur Kennlinie.
/* contact characteristic with smooth transition */
p(h) := sum(a[i]*h^i,i,0,2);
bc : [p(+epsilon)=0, subst([h=-epsilon],diff(p(h),h))=-1,subst([h=+epsilon],diff(p(h),h))=0];
coeff: solve(bc,[a[0],a[1],a[2]])[1];
kappa(h,epsilon) := if h>epsilon then 0 else if h<-epsilon then -h else epsilon/4-1/2*h+1/(4*epsilon)*h^2;
plot2d(kappa(h,0.25),[h,-1,1], [y,-0.1,1], [xlabel, "h/ε->"], [ylabel, "κ ->"])$
Kontaktkennlinie mit Verlustglied
Oft möchte man bei Kontaktkennlinen ein Verlustglied einbauen - also ein mathematisches Modell für einen Stoß, bei dem im Prozess der elastischen Deformation auch kinetische Energie verloren geht.
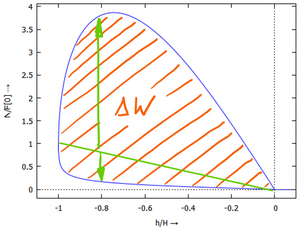
Dafür multiplizieren wir den Ausdruck für die Kraft F mit dem Geschwindigkeitsabhängigen Verlustglied l(v) - z.B. mit
- .
Maxima-Code
Zum Einbauen in Ihr Programm: der Quellcode zur Kennlinie.
/* Maxima */
/* contact characteristic */
/* piecewise linear with energy loss */
n(h,H) := if h<0 then -h/H else 0;
l(v,V) := if v<0 then 1*(1-v/V) else 1/(1+v/V);
motion: h=cos(2*%pi*τ);
motion: [motion, v=diff(subst(motion,h),τ)];
plot2d(subst(motion,n(h,1)*l(v,1)),[τ,0,1], [ylabel,"N/F[0] ->"], [xlabel,"t/T ->"])$
plot2d([parametric,subst(motion,h),subst(motion,n(h,1)*l(v,1)),[τ,0,1]], [ylabel,"N/F[0] →"], [xlabel,"h/H →"], [x,-1.1,0.1])$
Links: