Sources/Lexikon/Quaternionen für Drehungen: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
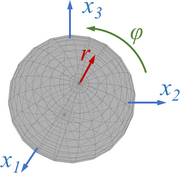
3D visualization einer Rotation bzgl. der Euler-Axe um den Winkel ϕ.
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 5: | Zeile 5: | ||
beschreiben. | beschreiben. | ||
Bei Einheits-Quaternionen gilt | Bei Einheits-Quaternionen gilt | ||
::<math>\displaystyle \sqrt{r_x^2 + r_y^2 + r_z^2} = 1</math> | ::<math>\displaystyle \sqrt{r_x^2 + r_y^2 + r_z^2} = 1</math>. | ||
Die Rotation wird dann durch das [[https://en.wikipedia.org/wiki/Tuple Quadruple]] | |||
::<math>\displaystyle \underline{q} = \left\[\cos\varphi, r_x\cdot\sin\varphi, r_y\cdot\sin\varphi, r_z\cdot\sin\varphi \right\]</math> | |||
erfasst. | |||
Die Transformationsmatrix können wir dann durch | |||
::<math>\underline{\underline{D}}_Q(\underline{q}(t)) = | |||
\begin{pmatrix}1-2 \left( {{{q_3}(t)}^{2}}+{{{q_2}(t)}^{2}}\right) & 2 \left( {q_1}(t) {q_2}(t)-{q_0}(t) {q_3}(t)\right) & 2 \left( {q_1}(t) {q_3}(t)+{q_0}(t) {q_2}(t)\right) \\ | |||
2 \left( {q_0}(t) {q_3}(t)+{q_1}(t) {q_2}(t)\right) & 1-2 \left( {{{q_3}(t)}^{2}}+{{{q_1}(t)}^{2}}\right) & 2 \left( {q_2}(t) {q_3}(t)-{q_0}(t) {q_1}(t)\right) \\ | |||
2 \left( {q_1}(t) {q_3}(t)-{q_0}(t) {q_2}(t)\right) & 2 \left( {q_2}(t) {q_3}(t)+{q_0}(t) {q_1}(t)\right) & 1-2 \left( {{{q_2}(t)}^{2}}+{{{q_1}(t)}^{2}}\right) \end{pmatrix} | |||
</math> | |||
abgebildet. | |||
Version vom 3. April 2022, 15:45 Uhr
Einheits-Quaternionen sind ein probates Werkzeug, um die räumliche Orientierung von Körpern zu beschreiben und räumliche Drehungen durchzuführen.

Dabei wird die Rotation durch einen Drehwinkel ϕ um eine Rotationsachse
beschreiben. Bei Einheits-Quaternionen gilt
- .
Die Rotation wird dann durch das [Quadruple]
- Fehler beim Parsen (Syntaxfehler): {\displaystyle \displaystyle \underline{q} = \left\[\cos\varphi, r_x\cdot\sin\varphi, r_y\cdot\sin\varphi, r_z\cdot\sin\varphi \right\]}
erfasst.
Die Transformationsmatrix können wir dann durch
abgebildet.