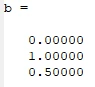Sources/Lexikon/Octave: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 2: | Zeile 2: | ||
Beispiel: | Beispiel: | ||
<syntaxhighlight lang="Matlab" line start=1> | |||
% für alpha = 30° | % für alpha = 30° | ||
alpha = pi/6 | alpha = pi/6 | ||
</syntaxhighlight> | |||
[[Datei:Octave-01.png|rahmenlos]] | [[Datei:Octave-01.png|rahmenlos]] | ||
<syntaxhighlight lang="Matlab" line start=1> | |||
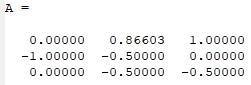
% System-Matrix | % System-Matrix | ||
A=[[ 0, cos(alpha), 1 ]; | A=[[ 0, cos(alpha), 1 ]; | ||
[-1,-sin(alpha), 0 ]; | [-1,-sin(alpha), 0 ]; | ||
[ 0,-sin(alpha),-1/2] ] | [ 0,-sin(alpha),-1/2] ] | ||
</syntaxhighlight> | |||
[[Datei:Octave-02.png|rahmenlos]] | [[Datei:Octave-02.png|rahmenlos]] | ||
<syntaxhighlight lang="Matlab" line start=1> | |||
% rechte Seite | % rechte Seite | ||
b=[ 0 ; | b=[ 0 ; | ||
1 ; | 1 ; | ||
1/2] | 1/2] | ||
</syntaxhighlight> | |||
[[Datei:Octave-03.png|rahmenlos]] | [[Datei:Octave-03.png|rahmenlos]] | ||
<syntaxhighlight lang="lisp" line start=1> | |||
% lösen ... (intern mit LU-Faktorisierung) | % lösen ... (intern mit LU-Faktorisierung) | ||
S=linsolve(A,b) | S=linsolve(A,b) | ||
</syntaxhighlight> | |||
[[Datei:Octave-04.png|rahmenlos]] | [[Datei:Octave-04.png|rahmenlos]] | ||