Sources/Lexikon/Phasendiagramme: Unterschied zwischen den Versionen
Die Seite wurde neu angelegt: „lklkj“ |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
Bei Systemen mit zwei [[Sources/Lexikon/Zustandsgröße|Zustandsgrößen]] können wir ihren Zustandsraum komplett in einem Phasendiagramm darstellen. Dabei wird bei mechanischen Systemen meist die Geschwindigkeit über dem Ort aufgetragen. | |||
Während Bewegungen linearer Differentialgleichungen immer durch [[Werkzeuge/Lösungsbausteine der Mathematik/Eigenwertprobleme#Das klassische Eigenwertproblem|Eigenwerte]] und Eigenvektoren bestimmt sind, fehlt bei nichtlinearen Bewegungen solche einfachen Charakter-Eigenschaften. Phasendiagramme sind eine Möglichkeit, nichtlineare Bewegungen besser zu verstehen. | |||
== Beispiel eines konservativen Schwingers == | |||
Ein konservativer (hier der Einfachheit halber linearer) Schwinger hat die Bewegungsgleichung zweiter Ordnung | |||
<math>\ddot{u} + \omega_0^2\cdot u = 0</math> . | |||
Eine Lösung ist | |||
<math>u(t) = u_0\cdot \sin(t) \text{ für } \omega_0=1</math>. | |||
[[Datei:Phasendiagramm-01.png|mini|150x150px|Phasendiagramm]] | |||
Das Diagramm | |||
<math>u(t) = u_0\cdot \sin(t) \text{ für } \omega_0=1</math> | |||
heißt Phasendiagramm. | |||
Merkmale von Phasendiagrammen. | |||
* Periodische Lösungen haben eine geschlossene Phasenkurven. | |||
* für v>0 wächst u, für v<0 nimmt u ab. | |||
== Phasendiagramm der Rayleigh-Differentialgleichung == | |||
Die Rayleigh-Differentialgleichung ist ein klassischer Vertreter nichtlinearer Differentialgleichungen. | |||
<math>\displaystyle \ddot{\varphi} - 2\cdot b\cdot\left(1 - \left(\frac{\dot{\varphi}}{a}\right)^2\right) \dot{\varphi} + \varphi = 0</math>. | |||
[[Datei:Phasendiagramm-02.png|mini|Vektorfeld]] | |||
Charakteristisch für das System ist: für | |||
<math>\displaystyle -1<\frac{\dot{\varphi}}{a}<+1</math> | |||
wird das System angefacht (es nimmt Energie auf), ansonsten wird es gedämpft (es dissipiert Energie). Das kann man gut im Phasendiagramm sehen: | |||
Hier ist das Phasendiagramm für zwei Anfangspunkte dargestellt. Die beiden Lösungen laufen in einen stabilen Grenzzyklus hinein. Das System hat also eine periodische Lösung. | |||
{{MyCodeBlock|title=Maxima für die Darstellung des Richtungsfeldes|text=Mima bietet mit <tt>plotdf<tt> eine Funktion, die das Richtungsfeld der Differentialgleichung darstellt.|code=}} | |||
[[Datei:Phasendiagramm-03.png|ohne|mini|Attraktoren und abstoßende Bereiche]] | |||
Die blauen Vektoren zeigen das Richtungsfeld der Differentialgleichung an. | |||
Version vom 21. April 2021, 12:49 Uhr
Bei Systemen mit zwei Zustandsgrößen können wir ihren Zustandsraum komplett in einem Phasendiagramm darstellen. Dabei wird bei mechanischen Systemen meist die Geschwindigkeit über dem Ort aufgetragen.
Während Bewegungen linearer Differentialgleichungen immer durch Eigenwerte und Eigenvektoren bestimmt sind, fehlt bei nichtlinearen Bewegungen solche einfachen Charakter-Eigenschaften. Phasendiagramme sind eine Möglichkeit, nichtlineare Bewegungen besser zu verstehen.
Beispiel eines konservativen Schwingers
Ein konservativer (hier der Einfachheit halber linearer) Schwinger hat die Bewegungsgleichung zweiter Ordnung
.
Eine Lösung ist
.
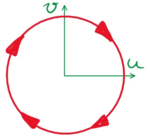
Das Diagramm
heißt Phasendiagramm.
Merkmale von Phasendiagrammen.
- Periodische Lösungen haben eine geschlossene Phasenkurven.
- für v>0 wächst u, für v<0 nimmt u ab.
Phasendiagramm der Rayleigh-Differentialgleichung
Die Rayleigh-Differentialgleichung ist ein klassischer Vertreter nichtlinearer Differentialgleichungen.
.
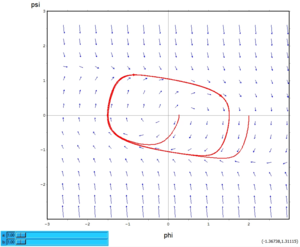
Charakteristisch für das System ist: für
wird das System angefacht (es nimmt Energie auf), ansonsten wird es gedämpft (es dissipiert Energie). Das kann man gut im Phasendiagramm sehen:
Hier ist das Phasendiagramm für zwei Anfangspunkte dargestellt. Die beiden Lösungen laufen in einen stabilen Grenzzyklus hinein. Das System hat also eine periodische Lösung.
Maxima für die Darstellung des Richtungsfeldes
Mima bietet mit plotdf eine Funktion, die das Richtungsfeld der Differentialgleichung darstellt.
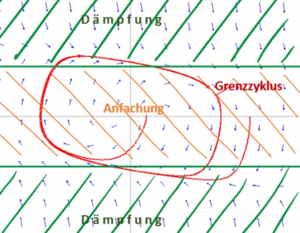
Die blauen Vektoren zeigen das Richtungsfeld der Differentialgleichung an.