Gelöste Aufgaben/UEBO: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 45: | Zeile 45: | ||
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des Problems , hier die Beträge der maximalen Auslenkung des Balkens für ''a = ℓ'' und der Verdrehung des Balkens am Momenten-Angriffspunkt für ''a = ℓ/2'': | Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des Problems , hier die Beträge der maximalen Auslenkung des Balkens für ''a = ℓ'' und der Verdrehung des Balkens am Momenten-Angriffspunkt für ''a = ℓ/2'': | ||
<table class="wikitable" style="background-color:white; float: left; margin-right:14px; | |||
"> | |||
<tr><th></th><th></th></tr> | |||
<tr><td></td><td></td></tr> | |||
</table> | |||
<math>W^{max} = \displaystyle \frac{M\,\ell^2}{9\sqrt{3}\,\cdot E\,I}</math> | <math>W^{max} = \displaystyle \frac{M\,\ell^2}{9\sqrt{3}\,\cdot E\,I}</math> | ||
| Zeile 67: | Zeile 74: | ||
==tmp== | ==tmp== | ||
<table class="wikitable" style="background-color:white; float: left; margin-right:14px; | |||
"> | |||
<tr><th>... für a=0</th><th>... für a=ℓ/2</th></tr> | |||
<tr><td></td><td></td></tr> | |||
<tr><td></td><td></td></tr> | |||
</table> | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
Version vom 19. April 2021, 06:10 Uhr
Aufgabenstellung
Diese Problemstellung liefert einen Näherungsansatz für eine Standardlösung zum Euler-Bernoulli-Balken.
Der Euler-Bernoulli-Balken AB wird durch ein Moment M zwischen den beiden gelenkigen Lagern belastet.
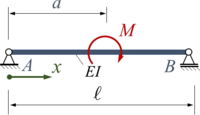
Gesucht ist eine Lösung für die Biegelinie mit dem Ansatz von Ritz und zwei Trial-Funktionen.
(Weg "1" wie in UEBH beschrieben.)
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
- dem Prinzip vom Minimum der Potentiellen Energie und
- Ansatzfunktionen über die gesamte Länge des Balkens.
tmp
Wir berechnen die Potentielle Energie U des Systems in Abhängigkeit von den generalisierten Koordinaten Wi und erhalten aus
die Gleichung für den gesuchten Koeffizienten Wi der Trial-Funktionen.
Header
Text
1+1
tmp
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des Problems , hier die Beträge der maximalen Auslenkung des Balkens für a = ℓ und der Verdrehung des Balkens am Momenten-Angriffspunkt für a = ℓ/2:
die maximale Auslenkung des Balkens für a=ℓ
die Verdrehung des Balkens am Momenten-Angriffspunkt für a=ℓ/2
Dimensionslose Orts-Koordinaten sind
.
Declarations
Text
1+1
tmp
| ... für a=0 | ... für a=ℓ/2 |
|---|---|
Formfunctions
Text
1+1
tmp
Potential Energy
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1
Links
- ...
Literature
- ...