Gelöste Aufgaben/UEBJ: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 9: | Zeile 9: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Der Euler-Bernoulli-Balken ''AB'' wird durch seine Gewichtskraft belastet. Er ist in ''A'' fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe ''h''. | |||
Für diese Aufgabe gibt es in UEBI eine analytische Lösung - hier schauen wir uns an, wie sich die Qualität der Näherungslösungen mit der Steigerung der Anzahl der Trial-Functions ändert. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:UEBF-01.png|250px|left|mini|Lageplan]] | [[Datei:UEBF-01.png|250px|left|mini|Lageplan]] | ||
Gesucht ist | Gesucht ist die Biegeline und Schnittkraftverläufe mit dem Ansatz von Ritz und mehreren Trial-Funktionen. | ||
</onlyinclude> | </onlyinclude> | ||
Gegeben sind für den Balken: | |||
== Lösung mit Maxima == | * Länge ''ℓ'', Breite ''b,'' | ||
* E-Modul ''E'', Dichte ''ρ'' und | |||
* die Höhe ''h''<sub>0</sub>''=b'' und ''h<sub>1</sub>'' jeweils in ''A'' und ''B''; dazwischen ist die Höhe linear veränderlich. | |||
==Lösung mit Maxima== | |||
Beim Verfahren von Ritz arbeiten wir mit | |||
* dem [[Werkzeuge/Gleichgewichtsbedingungen/Arbeitsprinzipe der Analytischen Mechanik/Prinzip vom Minimum der Potentiellen Energie|Prinzip vom Minimum der Potentiellen Energie]] und | |||
* [[Sources/Lexikon/Ansatzfunktion|Ansatzfunktionen]] über die gesamte Länge des Balkens. | |||
Um die Lösung dimensionslos zu machen, nutzen wir die [[Sources/Lexikon/Euler-Bernoulli-Balken/Standard-Lösungen#Kragbalken|analytische Lösung des einseitig fest eingespannten Balkens]] mit konstanten ''I'' unter einer konstanten Streckenlast ''q<sub>0</sub>''. Hier ist die maximale Auslenkung | |||
<math>\begin{array}{lcl} | |||
\displaystyle \hat{w} := \frac{q_{ref}\, \ell^4}{8 EI_{ref}} & | |||
\text{ mit }& | |||
q_{ref} = A_{ref}\, \rho\, g\\ | |||
&& | |||
A_{ref} = h_{ref}\cdot b \text{ und} \\ | |||
&& | |||
h_{ref} = \displaystyle \frac{h_0+h_1}{2} | |||
\end{array}</math>. | |||
Damit können wir uns die Lösungen dieses Problems als Vielfaches der analytischen Lösung eines ähnlichen Problems denken. | |||
==tmp== | ==tmp== | ||
| Zeile 37: | Zeile 61: | ||
<hr/> | <hr /> | ||
'''Links''' | '''Links''' | ||
* ... | *... | ||
'''Literature''' | '''Literature''' | ||
* ... | *... | ||
Version vom 17. April 2021, 06:09 Uhr
Aufgabenstellung
Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.
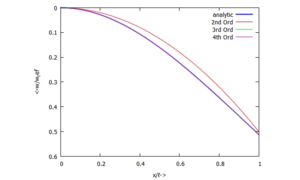
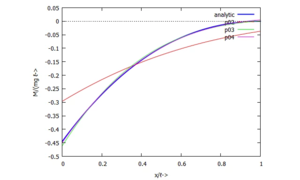
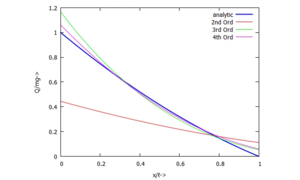
Für diese Aufgabe gibt es in UEBI eine analytische Lösung - hier schauen wir uns an, wie sich die Qualität der Näherungslösungen mit der Steigerung der Anzahl der Trial-Functions ändert.
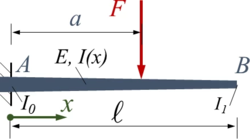
Gesucht ist die Biegeline und Schnittkraftverläufe mit dem Ansatz von Ritz und mehreren Trial-Funktionen.
Gegeben sind für den Balken:
- Länge ℓ, Breite b,
- E-Modul E, Dichte ρ und
- die Höhe h0=b und h1 jeweils in A und B; dazwischen ist die Höhe linear veränderlich.
Lösung mit Maxima
Beim Verfahren von Ritz arbeiten wir mit
- dem Prinzip vom Minimum der Potentiellen Energie und
- Ansatzfunktionen über die gesamte Länge des Balkens.
Um die Lösung dimensionslos zu machen, nutzen wir die analytische Lösung des einseitig fest eingespannten Balkens mit konstanten I unter einer konstanten Streckenlast q0. Hier ist die maximale Auslenkung
.
Damit können wir uns die Lösungen dieses Problems als Vielfaches der analytischen Lösung eines ähnlichen Problems denken.
tmp
Title
Text
1+1
Links
- ...
Literature
- ...
h