Gelöste Aufgaben/UEBI: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 237: | Zeile 237: | ||
... für ''w(ξ)'': | ... für ''w(ξ)'': | ||
[[Datei:UEBI-31.png|mini|Auslenkung ''w(x)''|alternativtext=|ohne]]... für ''ϕ(ξ)'': | [[Datei:UEBI-31.png|mini|Auslenkung ''w(x)''|alternativtext=|ohne]]{{MyDataBlock|title=Datenpunkte zum Plotten|data=1 | ||
2 | |||
3|text=table for Q(x)/(m g) ->}} | |||
... für ''ϕ(ξ)'': | |||
[[Datei:UEBI-32.png|mini|Querschnitts-Kippung ''w'(x)''|alternativtext=|ohne]]... für ''M(ξ)'': | [[Datei:UEBI-32.png|mini|Querschnitts-Kippung ''w'(x)''|alternativtext=|ohne]]... für ''M(ξ)'': | ||
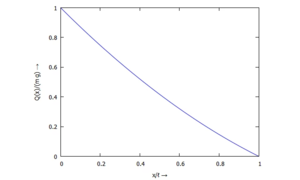
[[Datei:UEBI-33.png|mini|Momentenverlauf ''M(x)''|alternativtext=|ohne]]... für ''Q(ξ)'': | [[Datei:UEBI-33.png|mini|Momentenverlauf ''M(x)''|alternativtext=|ohne]]... für ''Q(ξ)'': | ||
Version vom 16. April 2021, 13:00 Uhr
Aufgabenstellung
Der Euler-Bernoulli-Balken AB wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt und hat eine konstante Breite b sowie eine zwischen A und B linear veränderliche Höhe h.
In UEBF haben wir eine Näherungslösung für dieses Problem berechnet.
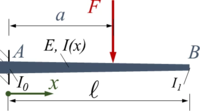
Gesucht ist die analytische Lösung des Problems.
Gegeben sind für den Balken:
- Länge ℓ, Breite b,
- E-Modul E, Dichte ρ und
- die Höhe h0=b und h1 jeweils in A und B; dazwischen ist die Höhe linear veränderlich.
Lösung mit Maxima
Um zur analytischen Lösung zukommen, müssen wir berücksichtigen, dass
.
Wir müssen also hier die Abhängigkeit der Querschnittseigenschaften von "x" in der Differentialbeziehung berücksichtigen. Das macht die Sache deutlich komplizierter als vorher.
tmp
Wir haben die Differential-Beziehungen
für die Querkraft Q, das Moment M, die Verkippung der Querschnitte ϕ und die Auslenkung w. Dabei ist die ortsabhängige Streckenlast
Die Höhe des Balkens ist linear veränderlich, nämlich
.
Header
Text
1+1
tmp
Diese Abkürzungen führen wir ein:
,
.
Für die Ergebnisse setzten wir dann exemplarisch
an - sonst werden die Ausdrücke zu umfangreich.
Declarations
Text
1+1
tmp
Beim Aufintegrieren der Differentialgleichungen stören die vielen dimensionsbehafteten Parameter. Viel einfacher werden die Gleichungen, wenn wir sie in dimensionsloser Form - mit dimensionsloser Auslenkung, Kippwinkel, Biegemoment und Querkraft anschreiben, also
.
Wir wählen dazu als Referenzlösung den Kragbalken mit konstantem Querschnitt unter konstanter Streckenlast, mit der maximalen Auslenkung
.
Als Referenz-Werte für die Streckenlast wählen wir hier die Werte unseres Balkens in x=ℓ/2, demnach
.
Die Differentialgleichungen werden dadurch und mit der dimensionslosen Ortskoordinate
viel einfacher, nämlich
.
Damit es übersichtlicher wird, lassen wir die Tilden über den gesuchten dimensionslosen Funktionen gleich wieder weg.
Dimensionless Form of Differential Equations
Text
1+1
tmp
Die Differentialbeziehungen lösen wir nun sukzessive zu
,
.
Bis hier ist alles wie gehabt - aber jetzt steht das ortsveränderliche Flächenmoment I(ξ) im Nenner. Maxima liefert
und im nächsten Schritt schließlich
.
Darin enthalten sind die unbekannten - also gesuchten - Integrationskonstanten
.
Integration Of Differential Equation
Text
1+1
tmp
Diese Unbekannten bestimmen wir aus den Randbedingungen, nämlich
und damit
.
Boundary Conditions
Text
1+1
tmp
Zum Lösen bringen wir die Gleichungen in die Form
,
die wir lösen zu
.
Solving
Text
1+1
tmp
Die Ergebnisse schauen wir uns in dimensionsloser Form an, wobei wir die Standard-Lösungen für den Balken unter konstanter Streckenlast ansetzen.
Für
finden wir
... für w(ξ):
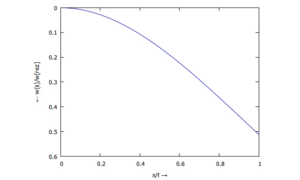
Datenpunkte zum Plotten
table for Q(x)/(m g) ->

toggle: data listing →
1
2
3... für ϕ(ξ):
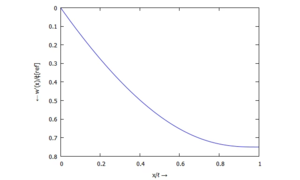
... für M(ξ):
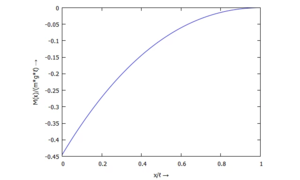
... für Q(ξ):
===Post-Processing===
Text
1+1
Links
- ...
Literature
- ...