Gelöste Aufgaben/UEBB: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Category:Gelöste Aufgaben]] | |||
[[Category:Dimensionslose Schreibweise]] | |||
[[Category:A*x=b]] | |||
[[Category:Numerische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Potential]] | |||
[[Category:Prinzip vom Minimum der Potentiellen Energie]] | |||
[[Category:Biege-Belastung]] | |||
[[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Rayleigh-Ritz-Prinzip]] | |||
[[Category:Matlab]] | |||
==Aufgabenstellung== | |||
<onlyinclude> | |||
[[Datei:UEBB-01.png|100px|left|mini|Caption]] | |||
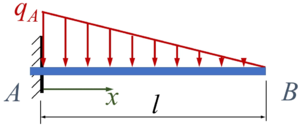
Der [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] AB wird durch eine linear veränderliche Streckenlast belastet. | |||
Gesucht ist die Lösung für ''w(x)'' mit dem Ansatz von Ritz und zwei Trial-Functions. | |||
</onlyinclude> | |||
== Lösung mit Matlab == | |||
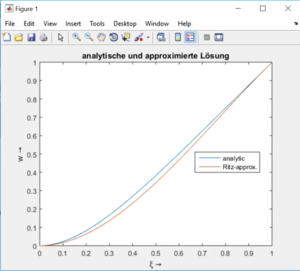
Für dieses Problem finden wir in der Literatur die tabellierte Musterlösung | |||
. | |||
Die verwenden wir als Referenz, um die Qualität unserer Näherungslösung zu bewerten. Die Auslenkung der analytischen Lösung ist am rechten Rand (x=l) ist maximal und beträgt | |||
Damit können wir die beiden Lösungen vergleichen und die Bewegungsgleichung nach Ritz dimensionslos machen. | |||
Für den Ritz-Ansatz brauchen wir die Terme der Potentiellen Energie des Systems | |||
, | |||
wobei Π die Formänderungsenergie ist und A die Arbeitsfunktion der äußeren Last q(x). | |||
Es ist | |||
Für den Ritz-Ansatz verwenden wir Ganzfeld-Ansätze - also Formfunktionen für die Näherung der exakten Lösung, die sich über die gesamte Balkenlänge erstrecken. | |||
Der Ansatz ist allgemein | |||
, | |||
wobei die ϕi die linear unabhängigen Formfunktionen und die Wi die Wichtungsfaktoren sind, die wir so bestimmen, dass die Gesamtlösung bestmöglich die gesuchte Funktion approximiert. | |||
Für die wählen wir ausschließlich Polynome - die können wir bequem differenzieren und integrieren. | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Potential Energy | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
[[Datei:UEBB-11.png|mini|Matlab: linsolve!]] | [[Datei:UEBB-11.png|mini|Matlab: linsolve!]] | ||
Version vom 13. April 2021, 08:36 Uhr
Aufgabenstellung
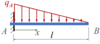
Der Euler-Bernoulli-Balken AB wird durch eine linear veränderliche Streckenlast belastet. Gesucht ist die Lösung für w(x) mit dem Ansatz von Ritz und zwei Trial-Functions.
Lösung mit Matlab
Für dieses Problem finden wir in der Literatur die tabellierte Musterlösung
.
Die verwenden wir als Referenz, um die Qualität unserer Näherungslösung zu bewerten. Die Auslenkung der analytischen Lösung ist am rechten Rand (x=l) ist maximal und beträgt
Damit können wir die beiden Lösungen vergleichen und die Bewegungsgleichung nach Ritz dimensionslos machen.
Für den Ritz-Ansatz brauchen wir die Terme der Potentiellen Energie des Systems
,
wobei Π die Formänderungsenergie ist und A die Arbeitsfunktion der äußeren Last q(x).
Es ist
Für den Ritz-Ansatz verwenden wir Ganzfeld-Ansätze - also Formfunktionen für die Näherung der exakten Lösung, die sich über die gesamte Balkenlänge erstrecken.
Der Ansatz ist allgemein
,
wobei die ϕi die linear unabhängigen Formfunktionen und die Wi die Wichtungsfaktoren sind, die wir so bestimmen, dass die Gesamtlösung bestmöglich die gesuchte Funktion approximiert.
Für die wählen wir ausschließlich Polynome - die können wir bequem differenzieren und integrieren.
tmp
Header
Text
1+1
tmp
Formfunctions
Text
1+1
tmp
Potential Energy
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1
Links
- ...
Literature
- ...