Gelöste Aufgaben/UEBA: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 11: | Zeile 11: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Wie man die Sensoren eines Smartphones für Messungen einsetzt, zeigen wir hier. | |||
Hier soll der Elastizitätsmodul des Stab-Materials mit Hilfe eines Biegeversuchs bestimmt werden. Der Stab der Länge ''ℓ'' hat einen quadratischen Querschnitt der Höhe ''h'' und die Masse ''m''. Für die Messung nutzen Sie als Sensor ihr Smartphone, das Ihnen die statische Beschleunigung ''a<sub>y</sub>, a<sub>z</sub>'' in ''y''- und ''z''-Richtung angibt. | |||
Sie haben Ihre [[Sources/Lexikon/Standard-Lösungen|Standard-Lösungen für den Euler-Bernoulli-Balken]] zu Hause vergessen und müssen sich mit einer Näherungslösung für den Balken nach dem Verfahren von Rayleigh-Ritz zufrieden geben. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:UEBA-01.png|300px|left|mini|Lageplan]] | [[Datei:UEBA-01.png|300px|left|mini|Lageplan]] | ||
Gesucht ist | Für den Versuch wird der Balken wird durch seine Gewichtskraft belastet. Er ist in ''A'' fest eingespannt, die Masse des Smartphones sei vernachlässigbar. | ||
Gesucht ist die Lösung mit dem Ansatz von Rayleigh-Ritz und zwei Trial-Functions. | |||
</onlyinclude> | </onlyinclude> | ||
Gegeben: ''ℓ=3 m, m=28 kg, g=9.81 m/s<sup>2</sup>, h=10 cm,'' | |||
'' a<sub>y</sub> ='' ''0.9793658 m/s<sup>2</sup>, a<sub>z</sub>='' ''9.7609909 m/s<sup>2</sup>'' | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Smartphones haben eine Reihe von Sensoren eingebaut - und die man kann als Ingenieur prima gebrauchen ... | |||
Ein Erklärungsvideo zu Beschleunigungs-Sensoren finden Sie [https://www.youtube.com/watch?v=KZVgKu6v808 hier]. | |||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Das Rayleigh-Ritz-Verfahren ist hier ein bisschen unter der experimentellen Bestimmung von Parametern des Systems "vergraben". | ||
Der Lösungsweg ist aber der gleiche wie gewohnt.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 34: | Zeile 48: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Streckenlast auf den Balken ist | ||
<math>\displaystyle q_0 = \frac{m\;g}{\ell}</math> | |||
und wir arbeiten mit der dimensionslosen Länge | |||
<math>\displaystyle \xi = \frac{x}{\ell}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=System-Parameters | {{MyCodeBlock|title=System-Parameters | ||
| Zeile 45: | Zeile 67: | ||
==tmp== | ==tmp== | ||
[[Datei:UEBA-12.png|mini|Formfunctions]] | |||
Als Ansatzfunktion für die Näherungslösung verwenden wir | |||
<math>\begin{array}{ll} | |||
\displaystyle w(x) = &&W\cdot \underbrace{\left( | |||
\xi^2\cdot(3-2\cdot\xi) \right) | |||
}_{\displaystyle =: \phi_1}\\ | |||
& + & | |||
\Phi\cdot \underbrace{\left( | |||
\xi^2\,\ell \cdot (\xi-1) \right) | |||
}_{\displaystyle =: \phi_2} | |||
\end{array}</math>.[[Datei:UEBA-11.png|mini|Koordinaten|alternativtext=|links]]Die Trial-Functions ''ϕ<sub>i</sub>'' erfüllen dabei die Bedingungen | |||
<math>w(\ell) = W</math> | |||
und | |||
<math>w'(\ell) = \Phi</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | {{MyCodeBlock|title=Formfunctions | ||
|text=Text | |text=Text | ||
| Zeile 57: | Zeile 98: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Für den Ritz-Ansatz brauchen wir die Terme der Potentiellen Energie des Systems | ||
<math>U = \Pi -A</math>, | |||
wobei '''''Π''''' die Formänderungsenergie ist und '''''A''''' die Arbeitsfunktion der äußeren Last ''q<sub>0</sub>''. | |||
Es ist | |||
<math>\begin{array}{ll} | |||
\Pi & = \displaystyle \frac{1}{2} \int_\ell EI\;(w'')^2 \,dx \\ | |||
A & = \displaystyle \int_\ell q(x) \cdot w(x) \, dx \text{ mit } q(x) = \frac{m\,g}{\ell}\end{array}</math>. | |||
'''''Π''''' und '''''A''''' setzen wir in '''''U''''' ein und schreiben die skalare Gleichung in Matrizenform an. Dabei müssen wir | |||
<math>\displaystyle \frac{d\phi_i}{x} = \frac{d\phi_i}{\xi} \cdot \underbrace{\displaystyle\frac{d\xi}{x}}_{\displaystyle = \frac{1}{\ell}}</math> | |||
beachten. Mit den gesuchten Größen | |||
<math>\underline{Q} = \left( | |||
\begin{array}{c} | |||
W\\ \Phi | |||
\end{array} | |||
\right)</math> | |||
erhalten wir für das Potential | |||
<math>U = \frac{1}{2} EI \cdot \displaystyle \underline{Q}^T \cdot \underline{\underline{K}}\cdot \underline{Q} - \underline{Q}^T\cdot \underline{P} </math> | |||
wobei für die Koeffizienten der Matrix ''K'' | |||
<math>k_{i,j} = \displaystyle \frac{EI}{\ell^3} \cdot \displaystyle \int_0^1 \phi_i''(\xi) \cdot \phi_j''(\xi) \, d\xi \text{ Achtung! Hier mit } (.)' = \frac{d(.)}{d\xi}</math> | |||
gilt und die rechten Seite ''P'' | |||
<math>\displaystyle p_i = q_0 \ell \cdot \int_0^1 \phi_i(\xi) \, d\xi</math>''.'' | |||
{{MyTip|title=Matlab© und Polynome|text=Alle verwendeten Funktionen in diesem Beispiel sind Polynome. Matlab© bietet für die Manipulation von Polynomen eine Klasse von Functions an, die hier sehr hilfreich sind: | |||
* [[Matlab©: Polynomials|https://de.mathworks.com/help/matlab/polynomials.htm]]}}<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Potential Energy | {{MyCodeBlock|title=Potential Energy | ||
|text=Text | |text=Text | ||
| Zeile 68: | Zeile 149: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Gleichgewichtsbedingungen | ||
<math>\displaystyle \frac{dU}{dQ_i} \stackrel{!}{=} 0</math> | |||
sind erfüllt, wenn | |||
<math>\displaystyle \frac{EI}{\ell^3} \cdot \begin{pmatrix}12 & -6 \ell \\ -6 \ell & 4 \ell^2\end{pmatrix}\cdot\begin{pmatrix}W\\ \Phi\end{pmatrix}= | |||
m\;g \cdot \begin{pmatrix}\displaystyle \frac{1}{2} \\ \displaystyle \frac{\ell}{12}\end{pmatrix}</math>. | |||
Dieses lineare Gleichungssystem hat die Lösung | |||
<math>\left( | |||
\begin{array}{c} | |||
W\\ | |||
\Phi | |||
\end{array} | |||
\right) = | |||
\displaystyle \frac{m\,g\,\ell^3}{EI} | |||
\left( | |||
\begin{array}{c} | |||
\displaystyle \frac{1}{8}\\ | |||
\displaystyle \frac{1}{6\,\ell} | |||
\end{array} | |||
\right)</math>. | |||
Zum Vergleich schauen wir jetzt bei der [[Sources/Lexikon/Standard-Lösungen|analytischen Lösung des Problems]] nach: | |||
<math>\begin{array}{lll} | |||
\hat{w} &= w_{max} &= \displaystyle \frac{\ell^4}{8\,EI}\cdot q_0\\ | |||
\hat{\varphi} &= w'_{B} &= \displaystyle \frac{\ell^3}{6\,EI}\cdot q_0 | |||
\end{array}</math>. | |||
Und sehen: unsere Lösung nach Rayleigh-Ritz stimmt am Rand exakt mit der analytischen Lösung überein, es ist | |||
<math>\begin{array}{ccc} | |||
W&=&\hat{w}\\ | |||
\Phi&=&\hat{\phi} | |||
\end{array}</math>!<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 78: | Zeile 199: | ||
==tmp== | ==tmp== | ||
[[Datei:UEBA-31.png|mini|Lösungsverläufe für ''w, φ, M, Q'']]Die Näherungslösung für Auslenkung ''w(x)'', Kippwinkel ''ϕ(x),'' Moment ''M(x)'' und Querkraft ''Q(x)'' können wir jetzt auftragen. Dafür verwenden wir die weiteren Referenzgrößen | |||
<math>\begin{array}{ll} | |||
M_{ref}&= m\,g\,\ell\\ | |||
Q_{ref}&= m\,g | |||
\end{array}</math> | |||
und tragen die Lösungen dimensionslos auf: | |||
Für unsere Fragestellung schreiben wir die Lösung um als | |||
<math>\begin{array}{ll} | |||
EI&= \displaystyle \frac{m\,g \,\ell^2}{6\, \Phi}\\ | |||
W&= \displaystyle \frac{3\,\Phi \ell}{4} | |||
\end{array}</math> | |||
und bestimmen uns den Drehwinkel aus den gemessenen statischen Beschleunigungen (vgl. Bild oben). Dabei ist | |||
<math>a_y = g \cdot \sin(\Phi)</math>. | |||
{{MyWarning|title=Warum nehmen wir nicht die z-Komponente der Beschleunigung?|text=Die az-Komponente können wir nicht gebrauchen weil | |||
::<math>\displaystyle \left.\frac{\partial a_z}{\partial \Phi} \right\vert_{\Phi=0} = 0</math>}} | |||
Da für kleine Winkel sin(Φ) ≈ Φ gilt, ist | |||
<math>\Phi = 0.1</math> | |||
Wir berechnen die gesuchte Materialkonstante mit | |||
<math>\displaystyle I = \frac{h^4}{12}</math> | |||
zu | |||
<math>\displaystyle E=878.976.000 \frac{N}{m^2}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text=Text | |text=Text | ||
| Zeile 95: | Zeile 248: | ||
<hr/> | <hr /> | ||
'''Links''' | '''Links''' | ||
* ... | * ... | ||
| Zeile 106: | Zeile 259: | ||
[[Datei:UEBA-01.png|mini|Lageplan]] | [[Datei:UEBA-01.png|mini|Lageplan]] | ||
Version vom 13. April 2021, 08:19 Uhr
Aufgabenstellung
Wie man die Sensoren eines Smartphones für Messungen einsetzt, zeigen wir hier.
Hier soll der Elastizitätsmodul des Stab-Materials mit Hilfe eines Biegeversuchs bestimmt werden. Der Stab der Länge ℓ hat einen quadratischen Querschnitt der Höhe h und die Masse m. Für die Messung nutzen Sie als Sensor ihr Smartphone, das Ihnen die statische Beschleunigung ay, az in y- und z-Richtung angibt.
Sie haben Ihre Standard-Lösungen für den Euler-Bernoulli-Balken zu Hause vergessen und müssen sich mit einer Näherungslösung für den Balken nach dem Verfahren von Rayleigh-Ritz zufrieden geben.
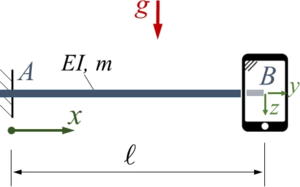
Für den Versuch wird der Balken wird durch seine Gewichtskraft belastet. Er ist in A fest eingespannt, die Masse des Smartphones sei vernachlässigbar.
Gesucht ist die Lösung mit dem Ansatz von Rayleigh-Ritz und zwei Trial-Functions.
Gegeben: ℓ=3 m, m=28 kg, g=9.81 m/s2, h=10 cm,
ay = 0.9793658 m/s2, az= 9.7609909 m/s2
Lösung mit Maxima
Smartphones haben eine Reihe von Sensoren eingebaut - und die man kann als Ingenieur prima gebrauchen ...
Ein Erklärungsvideo zu Beschleunigungs-Sensoren finden Sie hier.
tmp
Das Rayleigh-Ritz-Verfahren ist hier ein bisschen unter der experimentellen Bestimmung von Parametern des Systems "vergraben".
Der Lösungsweg ist aber der gleiche wie gewohnt.
Header
Text
1+1
tmp
Die Streckenlast auf den Balken ist
und wir arbeiten mit der dimensionslosen Länge
.
System-Parameters
Text
1+1
tmp
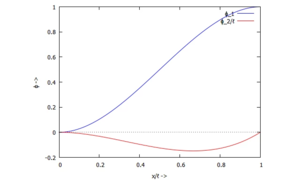
Als Ansatzfunktion für die Näherungslösung verwenden wir
.

Die Trial-Functions ϕi erfüllen dabei die Bedingungen
und
Formfunctions
Text
1+1
tmp
Für den Ritz-Ansatz brauchen wir die Terme der Potentiellen Energie des Systems
,
wobei Π die Formänderungsenergie ist und A die Arbeitsfunktion der äußeren Last q0.
Es ist
.
Π und A setzen wir in U ein und schreiben die skalare Gleichung in Matrizenform an. Dabei müssen wir
beachten. Mit den gesuchten Größen
erhalten wir für das Potential
wobei für die Koeffizienten der Matrix K
gilt und die rechten Seite P
.
| ✔ Matlab© und Polynome: |
| Alle verwendeten Funktionen in diesem Beispiel sind Polynome. Matlab© bietet für die Manipulation von Polynomen eine Klasse von Functions an, die hier sehr hilfreich sind: |
Potential Energy
Text
1+1
tmp
Die Gleichgewichtsbedingungen
sind erfüllt, wenn
.
Dieses lineare Gleichungssystem hat die Lösung
.
Zum Vergleich schauen wir jetzt bei der analytischen Lösung des Problems nach:
.
Und sehen: unsere Lösung nach Rayleigh-Ritz stimmt am Rand exakt mit der analytischen Lösung überein, es ist
!
Solving
Text
1+1
tmp
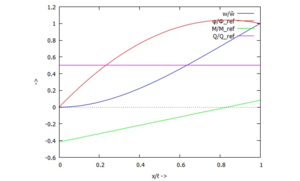
Die Näherungslösung für Auslenkung w(x), Kippwinkel ϕ(x), Moment M(x) und Querkraft Q(x) können wir jetzt auftragen. Dafür verwenden wir die weiteren Referenzgrößen
und tragen die Lösungen dimensionslos auf:
Für unsere Fragestellung schreiben wir die Lösung um als
und bestimmen uns den Drehwinkel aus den gemessenen statischen Beschleunigungen (vgl. Bild oben). Dabei ist
.
| 🧨 Warum nehmen wir nicht die z-Komponente der Beschleunigung?: |
| Die az-Komponente können wir nicht gebrauchen weil
|
Da für kleine Winkel sin(Φ) ≈ Φ gilt, ist
Wir berechnen die gesuchte Materialkonstante mit
zu
.
Post-Processing
Text
1+1
Links
- ...
Literature
- ...
