Gelöste Aufgaben/TC13: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 9: | Zeile 9: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Das System ist eine Variante von Aufgabe [[Gelöste Aufgaben/TC12|TC12]]. Hier ist eine Näherungslösung mit der [[Randwertprobleme/Methoden zur Lösung von Randwertproblemen/Finite Elemente Methode|Methode der Finiten Elemente]] gefragt. Das Sytem besteht aus zwei Sektionen mit den Längen ''ℓ<sub>1</sub>'' bzw. ''ℓ<sub>2</sub>'' sowie den Flächenmomenten ''I<sub>1</sub>'' bzw. ''I<sub>2</sub>''. Sektion ''AB'' ist durch eine konstante Streckenlast ''q<sub>0</sub>'' belastet, in ''B'' wirkt das Moment ''M<sub>B0</sub>''. Der Stab ist in ''A'' durch ein gelenkiges Festlager gelagert. In ''C'' ist das Stabende fest mit dem Umfang einer Rolle vom Radius ''r'' verbunden, die in ''D'' frei drehbar gelagert ist. In ''B'' sind die beiden Sektionen fest miteinander verbunden. Die Feder in ''B'' ist eine Translationsfeder mit der Steifigkeit ''<sub> </sub>k<sub>B</sub>''. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:TC12-01.png|300px|left|mini|Lageplan]] | [[Datei:TC12-01.png|300px|left|mini|Lageplan]] | ||
Gesucht ist | Gesucht ist die FEM-Lösung mit zwei Elementen für den Euler-Bernoulli-Balken. | ||
</onlyinclude> | </onlyinclude> | ||
Die Systemparameter sind die gleichen wie in TC12, das dort gesuchte Flächenmoment ''I<sub>1</sub>'' übernehmen wir zu | |||
<math>I_1 = 54\,000 \text{ mm}^4</math>. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title= | {{MyCodeBlock|title=Declarations | ||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Formfunctions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 34: | Zeile 92: | ||
<tr><td></td><td></td></tr> | <tr><td></td><td></td></tr> | ||
</table> | </table> | ||
[[Datei:TC13-11.png|mini|STruktur der Steifigkeitsmatrix.]] | |||
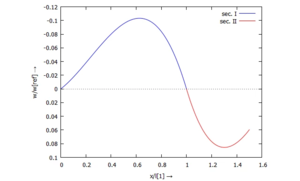
[[Datei:TC13-21.png|mini|Biegelinie ''w(x)'']] | |||
Version vom 9. April 2021, 06:16 Uhr
Aufgabenstellung
Das System ist eine Variante von Aufgabe TC12. Hier ist eine Näherungslösung mit der Methode der Finiten Elemente gefragt. Das Sytem besteht aus zwei Sektionen mit den Längen ℓ1 bzw. ℓ2 sowie den Flächenmomenten I1 bzw. I2. Sektion AB ist durch eine konstante Streckenlast q0 belastet, in B wirkt das Moment MB0. Der Stab ist in A durch ein gelenkiges Festlager gelagert. In C ist das Stabende fest mit dem Umfang einer Rolle vom Radius r verbunden, die in D frei drehbar gelagert ist. In B sind die beiden Sektionen fest miteinander verbunden. Die Feder in B ist eine Translationsfeder mit der Steifigkeit kB.
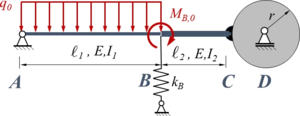
Gesucht ist die FEM-Lösung mit zwei Elementen für den Euler-Bernoulli-Balken.
Die Systemparameter sind die gleichen wie in TC12, das dort gesuchte Flächenmoment I1 übernehmen wir zu
.
Lösung mit Maxima
tmp
Header
Text
1+1
tmp
Declarations
Text
1+1
tmp
Formfunctions
Text
1+1
tmp
Equilibrium Conditions
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1

Links
- ...
Literature
- ...