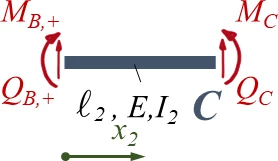Gelöste Aufgaben/TC12: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 7: | Zeile 7: | ||
==Aufgabenstellung== | ==Aufgabenstellung== | ||
Ein Stab ''ABC'' (E-Modul: ''E'') besteht aus zwei Sektionen mit den Längen ''ℓ<sub>1</sub>'' bzw. ''ℓ<sub>2</sub>'' sowie den Flächenmomenten ''I<sub>1</sub>'' bzw. ''I<sub>2</sub>''. Die Sektionen haben jeweils einen quadratischen Querschnitt, Sektion ''AB'' ist durch eine konstante Streckenlast ''q<sub>0</sub>'' belastet, in ''B'' wirkt das Moment ''M<sub>B0</sub>''. Der Stab ist in ''A'' durch ein gelenkiges Festlager gelagert. In ''C'' ist das Stabende fest mit dem Umfang einer Rolle vom Radius ''r'' verbunden, die in ''D'' frei drehbar gelagert ist. In ''B'' sind die beiden Sektionen fest miteinander verbunden. Die Feder in ''B'' ist eine Translationsfeder mit der Steifigkeit ''<sub> </sub>k<sub>B</sub>''. | |||
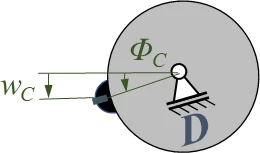
Interessant ist die kinematische Randbedingung aus der Rolle. | |||
<onlyinclude> | <onlyinclude> | ||
[[Datei:TC12-01.png|300px|left|mini|Lageplan]] | [[Datei:TC12-01.png|300px|left|mini|Lageplan]] | ||
Gesucht ist | Gesucht ist die Analytische Lösung für den [[Sources/Lexikon/Euler-Bernoulli-Balken|Euler-Bernoulli-Balken]] und die Verläufe der Schnittgrößen. | ||
</onlyinclude> | </onlyinclude>[[Datei:TC12-02.png|mini|Parameter]] | ||
Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter: | |||
Erstellen Sie dazu ein Programm, mit einem Euler-Bernoulli-Modell für die Berechnung der analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken. Bestimmen Sie Querschnitts-Abmessungen der Sektionen so, dass die maximale Auslenkung des Systems ''10 mm'' beträgt. | |||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
Die Aufgabe ist ein klassisches Randwertproblem: | |||
# zwei Gebiete, in denen ein Euler-Bernoulli-Balken in ''AB'' und ''BC'' durch eine Streckenlast ''q'' belastet ist (in Bereich II ist die Streckenlast allerdings Null) und somit durch die Differentialbeziehung | |||
<math>E\; I_i w_i^{IV}(x_i) = q(x_i) ,\;\; i=\{1,2\}</math> berschrieben wird. | |||
# Rand- und Übergangsbedingungen in den Punkten ''A, B, C'' | |||
Wir verwenden ''x<sub>i</sub>'' und ''ξ<sub>i</sub>'' als Koordinaten je Bereich, in der Übersicht sieht das Randwertproblem so aus: | |||
==tmp== | ==tmp== | ||
| Zeile 101: | Zeile 112: | ||
<hr/> | <hr /> | ||
'''Links''' | '''Links''' | ||
* ... | * ... | ||
| Zeile 114: | Zeile 125: | ||
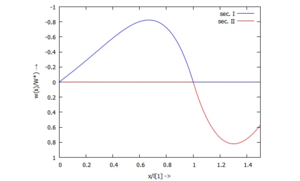
[[Datei:TC12-21.png|mini|Biegelinie ''w(x)'']] | [[Datei:TC12-21.png|mini|Biegelinie ''w(x)'']] | ||
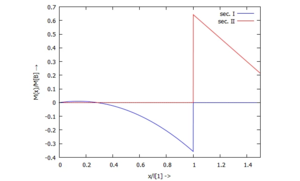
[[Datei:TC12-23.png|mini|Biegemoment ''M(x)'']] | [[Datei:TC12-23.png|mini|Biegemoment ''M(x)'']] | ||
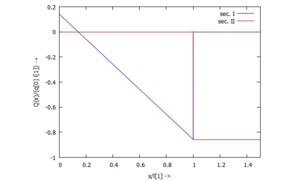
[[Datei:TC12-24.png|mini|Querkraft ''Q(x)'']] | [[Datei:TC12-24.png|mini|Querkraft ''Q(x)'']] | ||
[[Datei:TC12-01.png|mini|Lageplan]] | [[Datei:TC12-01.png|mini|Lageplan]] | ||
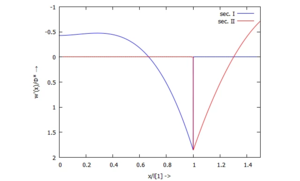
[[Datei:TC12-22.png|mini|Kippung ''w'(x)'']] | [[Datei:TC12-22.png|mini|Kippung ''w'(x)'']] | ||
Version vom 7. April 2021, 14:24 Uhr
Aufgabenstellung
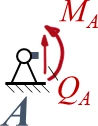
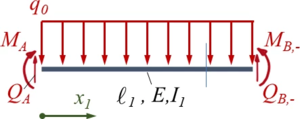
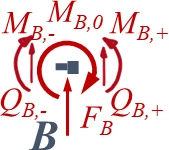
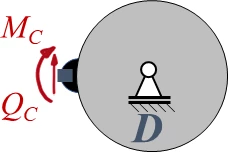
Ein Stab ABC (E-Modul: E) besteht aus zwei Sektionen mit den Längen ℓ1 bzw. ℓ2 sowie den Flächenmomenten I1 bzw. I2. Die Sektionen haben jeweils einen quadratischen Querschnitt, Sektion AB ist durch eine konstante Streckenlast q0 belastet, in B wirkt das Moment MB0. Der Stab ist in A durch ein gelenkiges Festlager gelagert. In C ist das Stabende fest mit dem Umfang einer Rolle vom Radius r verbunden, die in D frei drehbar gelagert ist. In B sind die beiden Sektionen fest miteinander verbunden. Die Feder in B ist eine Translationsfeder mit der Steifigkeit kB.
Interessant ist die kinematische Randbedingung aus der Rolle.
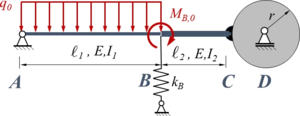
Gesucht ist die Analytische Lösung für den Euler-Bernoulli-Balken und die Verläufe der Schnittgrößen.

Ermitteln Sie für ein Euler-Bernoulli-Modell die analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken für diese Parameter:
Erstellen Sie dazu ein Programm, mit einem Euler-Bernoulli-Modell für die Berechnung der analytischen Verläufe der Schnittgrößen und Verschiebungen im Balken. Bestimmen Sie Querschnitts-Abmessungen der Sektionen so, dass die maximale Auslenkung des Systems 10 mm beträgt.
Lösung mit Maxima
Die Aufgabe ist ein klassisches Randwertproblem:
- zwei Gebiete, in denen ein Euler-Bernoulli-Balken in AB und BC durch eine Streckenlast q belastet ist (in Bereich II ist die Streckenlast allerdings Null) und somit durch die Differentialbeziehung
berschrieben wird.
- Rand- und Übergangsbedingungen in den Punkten A, B, C
Wir verwenden xi und ξi als Koordinaten je Bereich, in der Übersicht sieht das Randwertproblem so aus:
tmp
Header
Text
1+1
tmp
Declarations
Text
1+1
tmp
Generic Solutions for Euler-Bernoulli-Beam
Text
1+1
tmp
Boundary Conditions
Text
1+1
tmp
Prepare for Solver
Text
1+1
tmp
Solving
Text
1+1
tmp
Post-Processing
Text
1+1
Links
- ...
Literature
- ...