Gelöste Aufgaben/T313: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 22: | Zeile 22: | ||
In der Gleichgewichtsbedinung beim Prinzip der virtuellen Verrückungen | In der Gleichgewichtsbedinung beim Prinzip der virtuellen Verrückungen | ||
<math>\begin{array}{rl}\delta W =& \delta W^a - \delta\Pi\\\stackrel{!}{=}&0\end{array}</math> | |||
teilen wir | |||
<math>\displaystyle \Pi = \sum_i \delta\,\Pi_i</math> | |||
in die virtuelle Formänderungsenergie ''δΠ<sub>i</sub>'' je Stab auf. | |||
==tmp== | |||
Für die Aufgabe nutzen wir die Ergebnisse aus [[Gelöste Aufgaben/T312|T312]]. Dort haben wir die Anteile der viruellen Formänderungsenergievon | |||
<math>\delta\Pi_i</math> | |||
allgemein aufgeschrieben.[[Datei:T313-11.png|mini|Bezeichnung von Stäben und Knoten]]Den Stäben und Knoten geben wir Nummern - so können wir sie leichter ansprechen.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text=Text | |text=Text | ||
| Zeile 43: | Zeile 48: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Aus dem Lageplan lesen wir paarweise die x/y-Koordinaten der Knotenpunkte ''I, II, III, IV'' ab: | ||
{{MyCodeBlock|title= | |||
<math>\begin{array}{lll}N = [&[0,&0 ],\\ &[2a,&a ],\\ &[2a,&0],\\ &[4a,&0 ]\;]\end{array}</math>. | |||
Für die Stäbe erfassen wir die Nummern Ihrer Start- und End-Knotenpunkte: | |||
<math>\begin{array}{ll}R = [& [1,2]\\&[1,3]\\&[2,3]\\&[2,4]\\&[3,4]\;]\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Parameter | |||
|text=Text | |text=Text | ||
|code= | |code= | ||
| Zeile 54: | Zeile 66: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Aus diesen Parametern können wir alle Elemente der Element-Steifigkeitsmatrix ''K<sub>E</sub>'' | ||
<math>\delta\Pi_i=[{{\mathit{\delta\,u}}_{k}},{{\mathit{\delta\,v}}_{k}},{{\mathit{\delta\,u}}_{l}},{{\mathit{\delta\,v}}_{l}}]\cdot \underbrace{{{k}_{i}}\cdot \begin{pmatrix}{{\xi}_{x}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{x}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}}\\ {{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}}\\ -{{\xi}_{x}^{2}} & -{{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{x}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}}\\ -{{\xi}_{x}}\cdot {{\xi}_{y}} & -{{\xi}_{y}^{2}} & {{\xi}_{x}}\cdot {{\xi}_{y}} & {{\xi}_{y}^{2}}\end{pmatrix}}_{ \displaystyle =:\underline{\underline{K}}_E }\cdot \begin{pmatrix}{{u}_{k}}\\ {{v}_{k}}\\ {{u}_{l}}\\ {{v}_{l}}\end{pmatrix} | |||
</math>(vgl. [[Gelöste Aufgaben/T312|T312]]) | |||
je Stab berechnen.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Element Stiffness Matrix | {{MyCodeBlock|title=Element Stiffness Matrix | ||
|text=Text | |text=Text | ||
| Zeile 65: | Zeile 83: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die skalaren Gleichgewichtsbeziehungen können wir auch als | ||
<math>\underbrace{\delta\underline{Q}^T\cdot \underline{P}}_{\displaystyle = \delta W^a} - \underbrace{\delta\underline{Q}^T\cdot \underline{\underline{K}}\cdot \underline{Q}}_{\displaystyle = \delta\Pi} =0</math> | |||
schreiben. Die Gesamt-Steifigkeitsmatrix ''K'' aus dem Gesamt-Gleichungssystem | |||
<math>\underline{\underline{K}}\cdot\underline{Q} = \underline{P}</math> | |||
komponieren wir gleich aus den jeweiligen Element-Steifigkeitsmatrizen je Stab. "Komponieren", weil wir dabei nichts mehr berechnen müssen, sondern die Elemente der Element-Steifigkeitsmatrix nur passend in die Gesamt-Steifigkeitsmatrix einsortieren müssen. | |||
Es sind | |||
<math>\underline{Q} = \left(\begin{array}{c}u_1\\v_1\\u_2\\v_2\\u_3\\v_3\\u_4\\v_4\end{array} \right), \;\; \delta\underline{Q} = \left(\begin{array}{c}\delta u_1\\\delta v_1\\\delta u_2\\\delta v_2\\\delta u_3\\\delta v_3\\\delta u_4\\\delta v_4\end{array} \right)</math> | |||
die Koordinaten der Verschiebungen der Knoten in ''x-'' und ''y-''Richtung und ihre Variationen (ohne Berücksichtigung der Lager-Bindungen) sowie | |||
<math>\underline{P} = F\cdot \left(\begin{array}{c}0\\0\\1\\0\\0\\-2\\0\\0\end{array} \right)</math> | |||
die Last-Spaltenmatrix mit den Kräften ''F, 2F'' auf das Stabwerk, die aus | |||
<math>\delta W^a = F\cdot \delta u_2 + (- 2F)\cdot \delta v_3</math> | |||
kommt. | |||
Beim Komponieren der Gesamt-Steifigkeitsmatrix gehen wir so vor: | |||
Die virtuellen Formänderungs-Energien des Stabwerks setzen sich additiv aus den (hier fünf) virtuellen Formänderungsenergien je Stab zusammen: | |||
<math>\delta\Pi = \delta\Pi_1 + \delta\Pi_2 + ...\delta\Pi_i+ ... + \delta\Pi_5</math> | |||
Jedes Matrix-Element der Element-Steifigkeitsmatrix für den Stab ''i'' gehört nun zu genau einer Kombination aus Verschiebung und virtueller Verschiebung. So taucht in Liste der Summanden für Stab 1 (Knoten ''I'' und ''II'')auch der Term | |||
<math>\delta\Pi_i = ... + \delta v_1 \cdot k_{23} \cdot \delta u_2 + ...</math> | |||
auf. [[Datei:T313-12.png|mini|Einarbeiten der Element-Steifigkeitsmatrix|alternativtext=|500x500px]]Diesen müssen wir jetzt zur Gesamt-Steifigkeitsmatrix hinzuaddieren - so wie unten beschreiben. | |||
Die Gesamt-Steifigkeitsmatrix erhalten wir schließlich zu | |||
<math>\underline{\underline{K}} = \displaystyle\frac{EA}{a}\;\begin{pmatrix}\frac{8+{{5}^{\frac{3}{2}}}}{2\cdot {{5}^{\frac{3}{2}}}} & \frac{2}{{{5}^{\frac{3}{2}}}} & -\frac{4}{{{5}^{\frac{3}{2}}}} & -\frac{2}{{{5}^{\frac{3}{2}}}} & -\frac{1}{2} & 0 & 0 & 0\\ \frac{2}{{{5}^{\frac{3}{2}}}} & \frac{1}{{{5}^{\frac{3}{2}}}} & -\frac{2}{{{5}^{\frac{3}{2}}}} & -\frac{1}{{{5}^{\frac{3}{2}}}} & 0 & 0 & 0 & 0\\ -\frac{4}{{{5}^{\frac{3}{2}}}} & -\frac{2}{{{5}^{\frac{3}{2}}}} & \frac{8}{{{5}^{\frac{3}{2}}}} & 0 & 0 & 0 & -\frac{4}{{{5}^{\frac{3}{2}}}} & \frac{2}{{{5}^{\frac{3}{2}}}}\\ -\frac{2}{{{5}^{\frac{3}{2}}}} & -\frac{1}{{{5}^{\frac{3}{2}}}} & 0 & \frac{2+{{5}^{\frac{3}{2}}}}{{{5}^{\frac{3}{2}}}} & 0 & -1 & \frac{2}{{{5}^{\frac{3}{2}}}} & -\frac{1}{{{5}^{\frac{3}{2}}}}\\ -\frac{1}{2} & 0 & 0 & 0 & 1 & 0 & -\frac{1}{2} & 0\\ 0 & 0 & 0 & -1 & 0 & 1 & 0 & 0\\ 0 & 0 & -\frac{4}{{{5}^{\frac{3}{2}}}} & \frac{2}{{{5}^{\frac{3}{2}}}} & -\frac{1}{2} & 0 & \frac{8+{{5}^{\frac{3}{2}}}}{2\cdot {{5}^{\frac{3}{2}}}} & -\frac{2}{{{5}^{\frac{3}{2}}}}\\ 0 & 0 & \frac{2}{{{5}^{\frac{3}{2}}}} & -\frac{1}{{{5}^{\frac{3}{2}}}} & 0 & 0 & -\frac{2}{{{5}^{\frac{3}{2}}}} & \frac{1}{{{5}^{\frac{3}{2}}}}\end{pmatrix} | |||
</math> | |||
Diese Zuordnung - oder Komposition - macht man in komplexeren Programmen - wie FEM-Software - mit Inzidenztabellen. | |||
Lösen müssen wir nun das lineare Gleichungssystem aus | |||
<math>\begin{array}{rl}\delta W^a - \delta\Pi &= 0\\\delta \underline{Q}^T\cdot\left(\underline{P}-\underline{\underline{K}}\cdot\underline{Q}\right)&=0 \text{ und damit }\\\underline{\underline{K}}\cdot\underline{Q} &= \underline{P}\end{array}</math> | |||
Würden wir versuchen, diese Gleichungssystem direkt zu lösen, würden wir allerdings scheitern, denn: | |||
* die Determinante von <math>\underline{\underline{K}}</math> ist Null, | |||
d.h. Zeilen oder Spalten der Matrix sind voneinander linear abhängig. | |||
{| class="wikitable" | |||
| | |||
|}<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Compose total Stiffness Matrix | {{MyCodeBlock|title=Compose total Stiffness Matrix | ||
|text=Text | |text=Text | ||
| Zeile 75: | Zeile 147: | ||
==tmp== | ==tmp== | ||
[[Datei:T313-13.png|mini|Randbedingungen einarbeiten|alternativtext=|500x500px]]Was noch fehlt: die Randbedingungen haben wir noch nicht eingearbeitet! Und die erhalten wir durch Streichen der betroffenen Zeilen und Spalten im Gleichungssystem. | |||
Übrig bleibt | |||
<math>\displaystyle \frac{EA}{a}\;\left( \begin{array}{llll} \frac{8}{{{5}^{\frac{3}{2}}}} & 0 & 0 & 0\\ 0 & \frac{2+{{5}^{\frac{3}{2}}}}{{{5}^{\frac{3}{2}}}} & 0 & -1\\ 0 & 0 & 1 & 0\\ 0 & -1 & 0 & 1 \end{array} \right) \cdot \left( \begin{array}{c} u_2\\ v_2\\ u_3\\ v_3\\ \end{array} \right) = \left( \begin{array}{c} F\\ 0\\ 0\\ -2F\\ \end{array} \right)</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Boundary Conditions | {{MyCodeBlock|title=Boundary Conditions | ||
|text=Text | |text=Text | ||
| Zeile 87: | Zeile 162: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Diese Gleichungssystem hat eine Lösung: | ||
<math>\displaystyle \begin{array}{lll} \displaystyle {{u}_{2}} \cdot \frac{F\;a}{EA}&=\frac{{{5}^{\frac{3}{2}}}}{8}&\approx 1.4\\ \displaystyle {{v}_{2}} \cdot \frac{EA}{F\;a}&=-\frac{125+2\cdot {{5}^{\frac{3}{2}}}}{{{5}^{\frac{3}{2}}}+2}&\approx -11.2\\ {{u}_{3}}&=0\\ \displaystyle {{v}_{3}} \cdot \frac{EA}{F\;a}&=-{{5}^{\frac{3}{2}}}-2&\approx -13.2 \end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 98: | Zeile 176: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | In einer Nachlaufrechnung können wir nun auch noch die Stabkräfte bestimmen: | ||
<math>\begin{array}{ll} S_1 &= \displaystyle -\frac{15\cdot a\cdot F}{4\cdot \mathit{EA}}\\ S_2 &= 0\\ S_3 &= \displaystyle \frac{2\cdot a\cdot F}{\mathit{EA}}\\ S_4 &= \displaystyle -\frac{25\cdot a\cdot F}{4\cdot \mathit{EA}}\\ S_5 &= 0 \end{array}</math><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
|text=Text | |text=Text | ||
| Zeile 120: | Zeile 201: | ||
'''Literature''' | '''Literature''' | ||
* ... | * ... | ||
Version vom 5. April 2021, 15:29 Uhr
Aufgabenstellung
Stäbe waren früher das zentrale Bauteil in Leichtbau-Konstruktionen. In dieser Aufgabe geht es um die Komposition der Gesamt-Steifigkeitsmatrix für ein Stabwerk. Das Stabwerk besteht aus 5 Stäben gleicher Dehnsteifigkeit EA und wird durch die Kräfte F, 2F belastet.
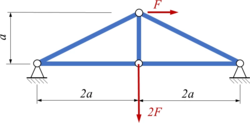
Gesucht sind Stabkräfte und Verschiebung der Knotenpunkte des Systems mit dem Prinzip der vertuellen Verrückungen.
Lösung mit Maxima
Dazu verwenden wir die Element-Steifigkeitsmatrix aus den Ergebnissen von Aufgabe T312.
In der Gleichgewichtsbedinung beim Prinzip der virtuellen Verrückungen
teilen wir
in die virtuelle Formänderungsenergie δΠi je Stab auf.
tmp
Für die Aufgabe nutzen wir die Ergebnisse aus T312. Dort haben wir die Anteile der viruellen Formänderungsenergievon
allgemein aufgeschrieben.
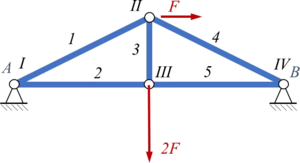
Den Stäben und Knoten geben wir Nummern - so können wir sie leichter ansprechen.
Header
Text
1+1
tmp
Aus dem Lageplan lesen wir paarweise die x/y-Koordinaten der Knotenpunkte I, II, III, IV ab:
.
Für die Stäbe erfassen wir die Nummern Ihrer Start- und End-Knotenpunkte:
.
Parameter
Text
1+1
tmp
Aus diesen Parametern können wir alle Elemente der Element-Steifigkeitsmatrix KE
(vgl. T312)
je Stab berechnen.
Element Stiffness Matrix
Text
1+1
tmp
Die skalaren Gleichgewichtsbeziehungen können wir auch als
schreiben. Die Gesamt-Steifigkeitsmatrix K aus dem Gesamt-Gleichungssystem
komponieren wir gleich aus den jeweiligen Element-Steifigkeitsmatrizen je Stab. "Komponieren", weil wir dabei nichts mehr berechnen müssen, sondern die Elemente der Element-Steifigkeitsmatrix nur passend in die Gesamt-Steifigkeitsmatrix einsortieren müssen.
Es sind
die Koordinaten der Verschiebungen der Knoten in x- und y-Richtung und ihre Variationen (ohne Berücksichtigung der Lager-Bindungen) sowie
die Last-Spaltenmatrix mit den Kräften F, 2F auf das Stabwerk, die aus
kommt.
Beim Komponieren der Gesamt-Steifigkeitsmatrix gehen wir so vor:
Die virtuellen Formänderungs-Energien des Stabwerks setzen sich additiv aus den (hier fünf) virtuellen Formänderungsenergien je Stab zusammen:
Jedes Matrix-Element der Element-Steifigkeitsmatrix für den Stab i gehört nun zu genau einer Kombination aus Verschiebung und virtueller Verschiebung. So taucht in Liste der Summanden für Stab 1 (Knoten I und II)auch der Term
auf.
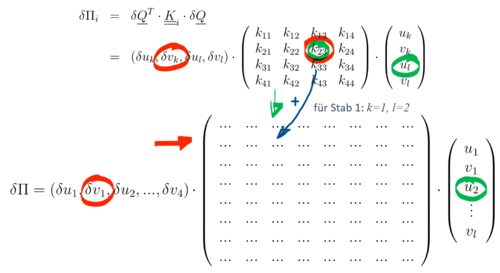
Diesen müssen wir jetzt zur Gesamt-Steifigkeitsmatrix hinzuaddieren - so wie unten beschreiben.
Die Gesamt-Steifigkeitsmatrix erhalten wir schließlich zu
Diese Zuordnung - oder Komposition - macht man in komplexeren Programmen - wie FEM-Software - mit Inzidenztabellen.
Lösen müssen wir nun das lineare Gleichungssystem aus
Würden wir versuchen, diese Gleichungssystem direkt zu lösen, würden wir allerdings scheitern, denn:
- die Determinante von ist Null,
d.h. Zeilen oder Spalten der Matrix sind voneinander linear abhängig.
Compose total Stiffness Matrix
Text
1+1
tmp
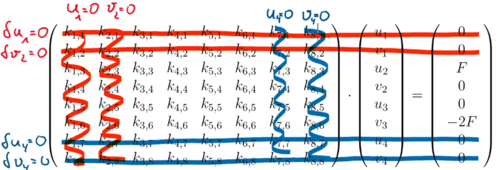
Was noch fehlt: die Randbedingungen haben wir noch nicht eingearbeitet! Und die erhalten wir durch Streichen der betroffenen Zeilen und Spalten im Gleichungssystem.
Übrig bleibt
Boundary Conditions
Text
1+1
tmp
Diese Gleichungssystem hat eine Lösung:
.
Solving
Text
1+1
tmp
In einer Nachlaufrechnung können wir nun auch noch die Stabkräfte bestimmen:
Post-Processing
Text
1+1
Links
- ...
Literature
- ...