Gelöste Aufgaben/SKEB: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
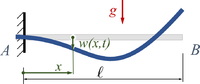
Lageplan
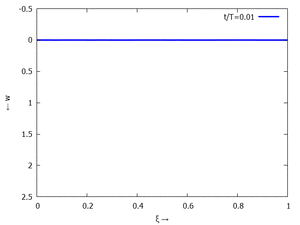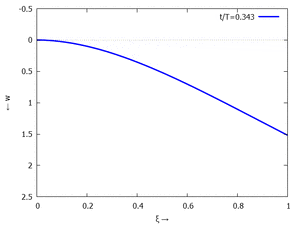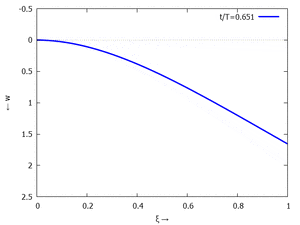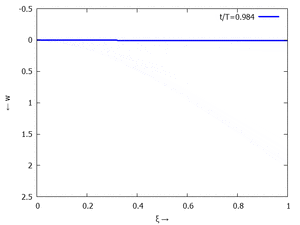
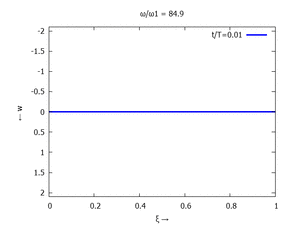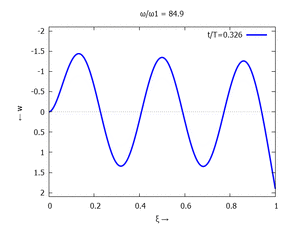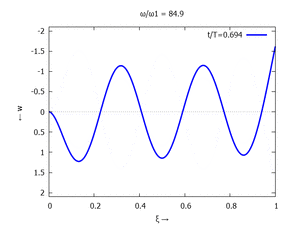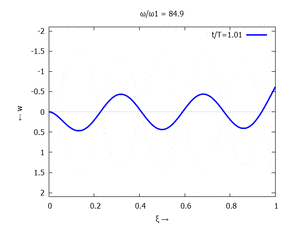
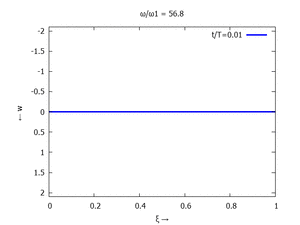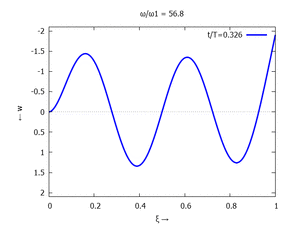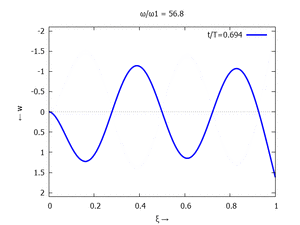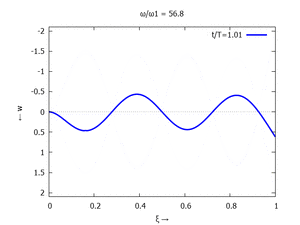
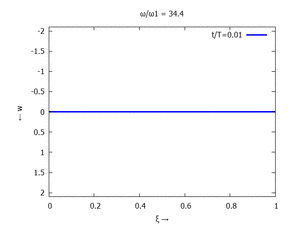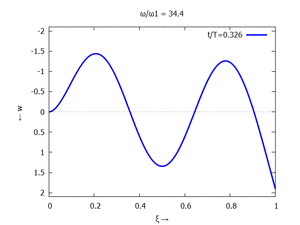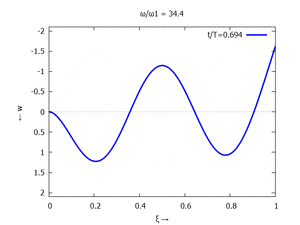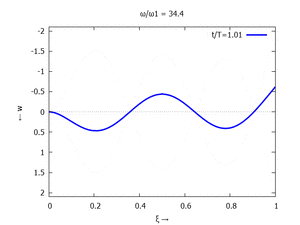
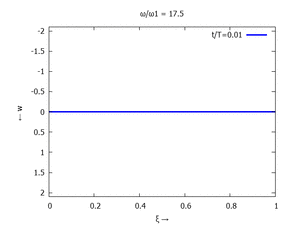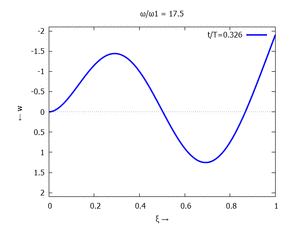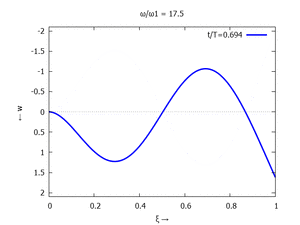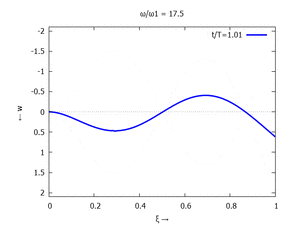
Animation: Loslassen des Systems aus der unverformten Rugelage. 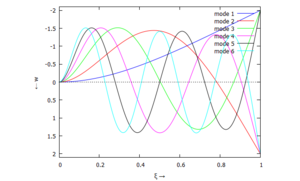
Modalformen 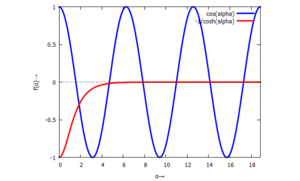
Nullstellensuche 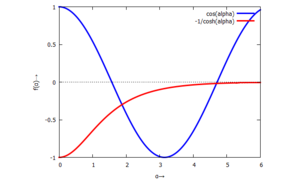
Nullstellensuche (Ausschnitt) 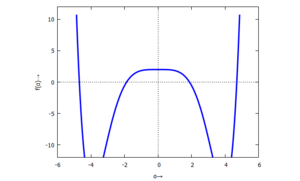
XXX 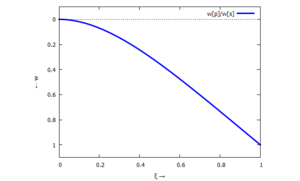
Statische Auslenkung 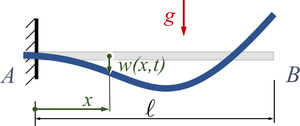
Lageplan
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 1: | Zeile 1: | ||
[[Datei:UEBE-mode- | [[Category:Gelöste Aufgaben]] | ||
[[Category:Analytische Lösung]] | |||
[[Category:Randwertproblem]] | |||
[[Category:Biege-Belastung]] | |||
[[Category:Euler-Bernoulli-Balken]] | |||
[[Category:Dynamik]] | |||
[[Category:Eigenvektor]][[Category:Eigenwert]][[Category:Eigenwertproblem]] | |||
[[Category:Maxima]] | |||
[[Category:Modalanalyse]] | |||
[[Category:Schwingungen von Kontinua]] | |||
==Aufgabenstellung== | |||
Die Bewegung des Balkens wird durch das Zusammenspiel von elastischen Verformungen und Trägheitskräften bestimmt. Man nennt das "Schwingungen von Kontinua" - diese untersuchen wir hier. Der zentrale Aufgabe besteht in der Berechnung der homogenen Lösung - und der Anpassung der Lösungsanteile an die Anfangsbedingungen. | |||
<onlyinclude> | |||
[[Datei:UEBE-01.png|200px|left|mini|Lageplan]] | |||
Gesucht ist analytische Lösung für Schwingungen des Euler-Bernoulli-Balkens beim Loslassen aus der enspannten Ruhelage. | |||
</onlyinclude> | |||
== Lösung mit Maxima == | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Header | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equations of Motion | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Particular Solution | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Homogeneous Solution | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
==tmp== | |||
<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Adapt to Initial Condition | |||
|text=Text | |||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
1+1 | |||
</syntaxhighlight> | |||
}} | |||
<table class="wikitable" style="background-color:white;"> | |||
<tr> | |||
<th>Mode</th><th>Modalform ϕ<sub>j</sub></th> | |||
<th>Mode</th><th>Modalform ϕ<sub>j</sub></th></tr> | |||
<tr> | |||
<td>'''#1'''<br/><math>\omega</math></td><td>[[Datei:UEBE-mode-1-animated.gif|rahmenlos]]</td> | |||
<td></td><td></td></tr> | |||
</table> | |||
<hr/> | |||
'''Links''' | |||
* ... | |||
'''Literature''' | |||
* ... | |||
[[Datei:UEBE-mode-6-animated.gif|rahmenlos]][[Datei:UEBE-mode-5-animated.gif|rahmenlos]][[Datei:UEBE-mode-4-animated.gif|rahmenlos]][[Datei:UEBE-mode-3-animated.gif|rahmenlos]][[Datei:UEBE-mode-2-animated.gif|rahmenlos]] | |||
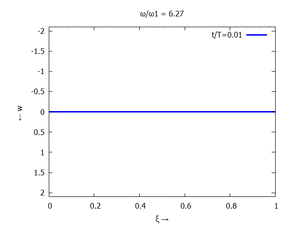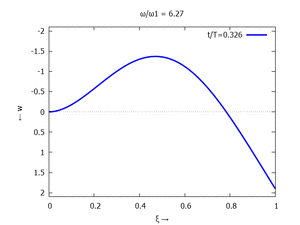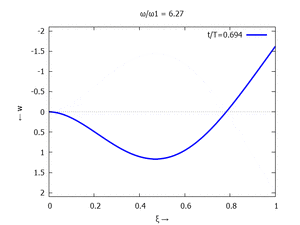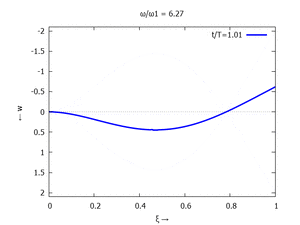
[[Datei:UEBE-initial-value-solution-animation.gif|mini|Animation: Loslassen des Systems aus der unverformten Rugelage.]] | [[Datei:UEBE-initial-value-solution-animation.gif|mini|Animation: Loslassen des Systems aus der unverformten Rugelage.]] | ||
[[Datei:UEBE-31.png|mini|Modalformen]] | [[Datei:UEBE-31.png|mini|Modalformen]] | ||
| Zeile 7: | Zeile 103: | ||
[[Datei:UEBE-11.png|mini|Statische Auslenkung]] | [[Datei:UEBE-11.png|mini|Statische Auslenkung]] | ||
[[Datei:UEBE-01.png|mini|Lageplan]] | [[Datei:UEBE-01.png|mini|Lageplan]] | ||
Version vom 2. April 2021, 13:54 Uhr
Aufgabenstellung
Die Bewegung des Balkens wird durch das Zusammenspiel von elastischen Verformungen und Trägheitskräften bestimmt. Man nennt das "Schwingungen von Kontinua" - diese untersuchen wir hier. Der zentrale Aufgabe besteht in der Berechnung der homogenen Lösung - und der Anpassung der Lösungsanteile an die Anfangsbedingungen.

Gesucht ist analytische Lösung für Schwingungen des Euler-Bernoulli-Balkens beim Loslassen aus der enspannten Ruhelage.
Lösung mit Maxima
tmp
Header
Text
1+1
tmp
Equations of Motion
Text
1+1
tmp
Particular Solution
Text
1+1
</syntaxhighlight
}}
==tmp==
<!-------------------------------------------------------------------------------->
{{MyCodeBlock|title=Homogeneous Solution
|text=Text
|code=
<syntaxhighlight lang="lisp" line start=1>
1+1
tmp
Adapt to Initial Condition
Text
1+1
| Mode | Modalform ϕj | Mode | Modalform ϕj |
|---|---|---|---|
| #1 | 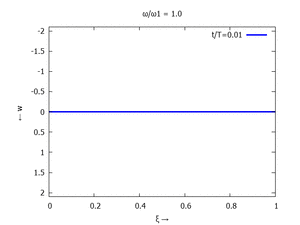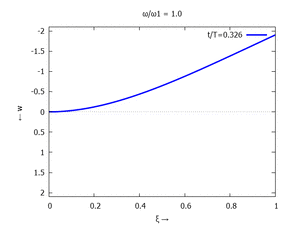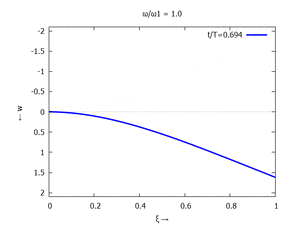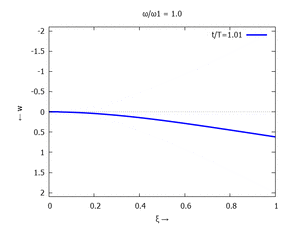 |
Links
- ...
Literature
- ...