Gelöste Aufgaben/LM01: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
Keine Bearbeitungszusammenfassung |
||
| Zeile 12: | Zeile 12: | ||
Wie [[Sources/Lexikon/Minimum Prinzipe|Minimum-Prinzipe]] "funktionieren" und wie die Mathematik dazu aussieht, untersuchen wir hier an einem klassischen Beispiel. | Wie [[Sources/Lexikon/Minimum Prinzipe|Minimum-Prinzipe]] "funktionieren" und wie die Mathematik dazu aussieht, untersuchen wir hier an einem klassischen Beispiel. | ||
<onlyinclude> | <onlyinclude> | ||
[[Datei: | [[Datei:LM01-01.png|alternativtext=|links|mini|250x250px|Lageplan]] | ||
Gesucht ist die Lage der Knoten von vier starren Kettengliedern (Länge ℓ, Masse m) im Erdschwerefeld. | Gesucht ist die Lage der Knoten von vier starren Kettengliedern (Länge ℓ, Masse m) im Erdschwerefeld. | ||
</onlyinclude> | </onlyinclude> | ||
| Zeile 34: | Zeile 34: | ||
==tmp== | ==tmp== | ||
[[Datei:LM01-02.png|mini|Koordinaten|alternativtext=|200x200px]]Jeder Verbindungspunkt eines Kettengliedes hat zwei Koordinaten ''U<sub>j</sub>, V<sub>j</sub>''. | |||
<!--------------------------------------------------------------------------------> | Die Arbeitsfunktion der Gewichtskraft ist | ||
::<math>\displaystyle A = \sum_{n=0}^N m\,g\, \frac{U_{i-1}-U_i}{2}</math>. | |||
Im Gleichgewicht hat diese Arbeitsfunktion ein Minimum, allerdings müssen dabei für die starren Kettenglieder die Bedingungen<blockquote><blockquote> | |||
<math>\left(U_{i} - U_{i-1}\right)^2 + \left(V_{i} - V_{i-1}\right)^2 = \ell^2</math> | |||
erfüllt sein!</blockquote></blockquote><!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Declarations | {{MyCodeBlock|title=Declarations | ||
|text=Text | |text=Text | ||
| Zeile 46: | Zeile 54: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Lagrange-Funktion für die Kette lautet also | ||
<math>\begin{array}{lll}\Lambda = &&\displaystyle \sum_{n=0}^N m\,g\, \frac{U_{i-1}-U_i}{2}\\& +&\displaystyle \sum_{n=0}^N \lambda_i\cdot \left(\left(U_{i} - U_{i-1}\right)^2 + \left(V_{i} - V_{i-1}\right)^2 - \ell^2 \right)\end{array}</math> | |||
mit den Lagrangeschen Multiplikatoren λ<sub>i</sub>. | |||
Hier ist ''N'' =4, die Randbedingungen für die Verschiebungen lauten also | |||
<math>U_0 = 0, U_4 = 0, V_0=0 \text{ und } V_N = L</math> | |||
und wir wählen hier | |||
<math>L = 3\,\ell</math>. | |||
Mit der Abkürzung | |||
<math>\gamma = m\, g\, \ell</math> und <math>U_i = \ell \; \tilde{U}_i, \;\;V_i = \ell \; \tilde{V}_i, </math> | |||
ist dann | |||
<math>\begin{array}{lll} \Lambda =&&\displaystyle \frac{\left( {\tilde{U}_3}+{\tilde{U}_2}\right) \gamma }{2}+\frac{{\tilde{U}_3} \gamma }{2}+\frac{\left( {\tilde{U}_2}+{\tilde{U}_1}\right) \gamma }{2}+\frac{{\tilde{U}_1} \gamma }{2}\\&+&\left( {{\left( 3-{\tilde{V}_3}\right) }^{2}}+{{\tilde{U}}_{3}^{2}}-1\right) \, {{\lambda }_4}\\&+&\left( {{\left( {\tilde{V}_3}-{\tilde{V}_2}\right) }^{2}}+{{\left( {\tilde{U}_3}-{\tilde{U}_2}\right) }^{2}}-1\right) \, {{\lambda }_3}\\&+&\left( {{\left( {\tilde{V}_2}-{\tilde{V}_1}\right) }^{2}}+{{\left( {\tilde{U}_2}-{\tilde{U}_1}\right) }^{2}}-1\right) \, {{\lambda }_2}\\&+&\left( {{\tilde{V}}_{1}^{2}}+{{\tilde{U}}_{1}^{2}}-1\right) \, {{\lambda }_1} \end{array}</math>. | |||
Die Gleichgewichtsbedingungen unter Nebenbedingungen lauten dann | |||
<math>\begin{array}{ll}\displaystyle \frac{\partial \Lambda}{\partial U_i}&=0\\\displaystyle \frac{\partial \Lambda}{\partial V_i}&=0\\\displaystyle \frac{\partial \Lambda}{\partial \lambda_i}&=0\end{array}</math>.<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Equilibrium Conditions | {{MyCodeBlock|title=Equilibrium Conditions | ||
|text=Text | |text=Text | ||
| Zeile 57: | Zeile 92: | ||
==tmp== | ==tmp== | ||
<!--------------------------------------------------------------------------------> | Die Gleichungen, die wir nun lösen müssen sind: | ||
<math>\begin{array}{ll} 0=&-2 {\tilde{U}_2}\, {{\lambda }_2}+2 {\tilde{U}_1}\, {{\lambda }_2}+2 {\tilde{U}_1}\, {{\lambda }_1}+1\\ 0=&-2 {\tilde{V}_2}\, {{\lambda }_2}+2 {\tilde{V}_1}\, {{\lambda }_2}+2 {\tilde{V}_1}\, {{\lambda }_1}\\ 0=&{{\tilde{V}}_{1}^{2}}+{{\tilde{U}}_{1}^{2}}-1\\ 0=&-2 {\tilde{U}_3}\, {{\lambda }_3}+2 {\tilde{U}_2}\, {{\lambda }_3}+2 {\tilde{U}_2}\, {{\lambda }_2}-2 {\tilde{U}_1}\, {{\lambda }_2}+1\\ 0=&-2 {\tilde{V}_3}\, {{\lambda }_3}+2 {\tilde{V}_2}\, {{\lambda }_3}+2 {\tilde{V}_2}\, {{\lambda }_2}-2 {\tilde{V}_1}\, {{\lambda }_2}\\ 0=&{{\tilde{V}}_{2}^{2}}-2 {\tilde{V}_1}\, {\tilde{V}_2}+{{\tilde{U}}_{2}^{2}}-2 {\tilde{U}_1}\, {\tilde{U}_2}+{{\tilde{V}}_{1}^{2}}+{{\tilde{U}}_{1}^{2}}-1\\ 0=&2 {\tilde{U}_3}\, {{\lambda }_4}+2 {\tilde{U}_3}\, {{\lambda }_3}-2 {\tilde{U}_2}\, {{\lambda }_3}+1\\ 0=&2 {\tilde{V}_3}\, {{\lambda }_4}-6 {{\lambda }_4}+2 {\tilde{V}_3}\, {{\lambda }_3}-2 {\tilde{V}_2}\, {{\lambda }_3}\\ 0=&{{\tilde{V}}_{3}^{2}}-2 {\tilde{V}_2}\, {\tilde{V}_3}+{{\tilde{U}}_{3}^{2}}-2 {\tilde{U}_2}\, {\tilde{U}_3}+{{\tilde{V}}_{2}^{2}}+{{\tilde{U}}_{2}^{2}}-1\\ 0=&{{\tilde{V}}_{3}^{2}}-6 {\tilde{V}_3}+{{\tilde{U}}_{3}^{2}}+8\end{array}</math>. | |||
Und die sind nichtlinear! Dafür brauchen wir eine Lösungsroutine - wir verwenden das Newton–Verfahren. | |||
Wir finden: | |||
<math>\begin{array}{lll} {\tilde{U}_1}=&&0.807\\ {\tilde{V}_1}=&&0.59\\ {{\lambda }_1}=&-&0.929\\ {\tilde{U}_2}=&&1.22\\ {\tilde{V}_2}=&&1.5\\ {{\lambda }_2}=&-&0.603\\ {\tilde{U}_3}=&&0.807\\ {\tilde{V}_3}=&&2.41\\ {{\lambda }_3}=&-&0.603\\ {{\lambda }_4}=&-&0.929\end{array}</math>. | |||
{{MyTip|title=Lösungen nichtlinearer Gleichungen|text=... sind eine Wissenschaft für sich. Selbst für scheinbar triviale Probleme wie dieses laufen wir für N>4 schon in große numerische Probleme hinein. Der Trick ist häufig, als Startpunkt der Iteration Werte vorzugeben, die einigermaßen in der Nähe der erwarteten Lösung liegen. Sonst verabschiedet sich der Newton-Algorithmus oft mit einem "convergance error". | |||
Oder wir finden Lösungen, die zwar Gleichgewichtsbedingungen sind aber offensichtlich instabil sind.}}<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Solving | {{MyCodeBlock|title=Solving | ||
|text=Text | |text=Text | ||
| Zeile 67: | Zeile 115: | ||
==tmp== | ==tmp== | ||
[[Datei:LM01-11.png|mini|Lösungskonstellation]]Hier erhalten wir jedoch eine Lösung - und so sieht sie aus;<!--------------------------------------------------------------------------------> | |||
{{MyCodeBlock|title=Post-Processing | {{MyCodeBlock|title=Post-Processing | ||
| Zeile 83: | Zeile 132: | ||
<tr><td></td><td></td></tr> | <tr><td></td><td></td></tr> | ||
</table> | </table> | ||
<hr/> | <hr /> | ||
'''Links''' | '''Links''' | ||
* ... | *... | ||
'''Literature''' | '''Literature''' | ||
* ... | *... | ||
Version vom 1. April 2021, 07:22 Uhr
Aufgabenstellung
Wie Minimum-Prinzipe "funktionieren" und wie die Mathematik dazu aussieht, untersuchen wir hier an einem klassischen Beispiel.
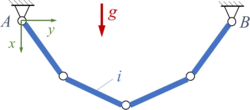
Gesucht ist die Lage der Knoten von vier starren Kettengliedern (Länge ℓ, Masse m) im Erdschwerefeld.
Lösung mit Maxima
Lorem Ipsum ....
tmp
Die Aufgabe ist ein einfaches Beispiel für Lösungsansätze mit "Lagrange-Multiplikatoren".
Wir arbeiten mit dem Prinzip vom Minimum der Potentiellen Energie - also dem Potential der Gewichtskraft der Kettenglieder. Besonders charmant - im Vergleich zu Ansätzen mit dem Kräfte-Gleichgewicht ist hier das "Wegfallen" der Schnittkräfte - die brauchen wir hier nicht explizit angeben.
Header
Text
1+1
tmp
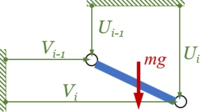
Jeder Verbindungspunkt eines Kettengliedes hat zwei Koordinaten Uj, Vj.
Die Arbeitsfunktion der Gewichtskraft ist
- .
Im Gleichgewicht hat diese Arbeitsfunktion ein Minimum, allerdings müssen dabei für die starren Kettenglieder die Bedingungen
erfüllt sein!
Declarations
Text
1+1
tmp
Die Lagrange-Funktion für die Kette lautet also
mit den Lagrangeschen Multiplikatoren λi.
Hier ist N =4, die Randbedingungen für die Verschiebungen lauten also
und wir wählen hier
.
Mit der Abkürzung
und
ist dann
.
Die Gleichgewichtsbedingungen unter Nebenbedingungen lauten dann
.
Equilibrium Conditions
Text
1+1
tmp
Die Gleichungen, die wir nun lösen müssen sind:
.
Und die sind nichtlinear! Dafür brauchen wir eine Lösungsroutine - wir verwenden das Newton–Verfahren.
Wir finden:
.
| ✔ Lösungen nichtlinearer Gleichungen: |
| ... sind eine Wissenschaft für sich. Selbst für scheinbar triviale Probleme wie dieses laufen wir für N>4 schon in große numerische Probleme hinein. Der Trick ist häufig, als Startpunkt der Iteration Werte vorzugeben, die einigermaßen in der Nähe der erwarteten Lösung liegen. Sonst verabschiedet sich der Newton-Algorithmus oft mit einem "convergance error". Oder wir finden Lösungen, die zwar Gleichgewichtsbedingungen sind aber offensichtlich instabil sind. |
Solving
Text
1+1
tmp
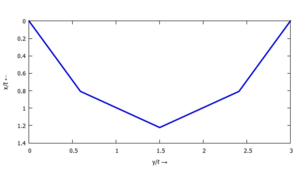
Hier erhalten wir jedoch eine Lösung - und so sieht sie aus;
Post-Processing
Text
1+1
Links
- ...
Literature
- ...