Gelöste Aufgaben/Kw60: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung |
|||
| Zeile 21: | Zeile 21: | ||
== Lösung mit Maxima == | == Lösung mit Maxima == | ||
<!--------------------------------------------------------------------------------> | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Header | {{MyCodeBlock|title=Header | ||
|text= | |text= | ||
Das Modell erstellen wir mit der [[Sources/Anleitungen/FEM-Formulierung für den Euler-Bernoulli-Balken|FEM-Formulierung für den Euler-Bernoulli-Balken]] mit zwei Elementen. | |||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/*******************************************************/ | |||
/* MAXIMA script */ | |||
/* version: wxMaxima 15.08.2 */ | |||
/* author: Andreas Baumgart */ | |||
/* last updated: 2019-09-01 */ | |||
/* ref: TMC */ | |||
/* description: simple EBB with two section */ | |||
/* solved as FE Problem */ | |||
/*******************************************************/ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | <!--------------------------------------------------------------------------------> | ||
Zum späteren Plotten verwenden wir Referenzgrößen, die wir der analytischen Standard-Lösung eines Kragbalkens entnehmen. | {{MyCodeBlock|title=Declarations | ||
|text= | |||
Zum späteren Plotten verwenden wir Referenzgrößen, die wir der analytischen [[Sources/Lexikon/Standard-Lösungen|Standard-Lösung]] eines Kragbalkens entnehmen. | |||
Dies sind | Dies sind | ||
<math>\begin{array}{ccl} | ::<math>\begin{array}{ccl} | ||
{{W}_{\mathit{ref}}}&=&\displaystyle \frac{{{q}_{0}}\cdot {{\ell}_{0}^{4}}}{8\cdot {{I}_{0}}\cdot E},\\ | {{W}_{\mathit{ref}}}&=&\displaystyle \frac{{{q}_{0}}\cdot {{\ell}_{0}^{4}}}{8\cdot {{I}_{0}}\cdot E},\\ | ||
{{\Phi}_{\mathit{ref}}}&=&\displaystyle\frac{{{q}_{0}}\cdot {{\ell}_{0}^{3}}}{6\cdot {{I}_{0}}\cdot E},\\ | {{\Phi}_{\mathit{ref}}}&=&\displaystyle\frac{{{q}_{0}}\cdot {{\ell}_{0}^{3}}}{6\cdot {{I}_{0}}\cdot E},\\ | ||
| Zeile 49: | Zeile 56: | ||
Wir verwenden dimensionslose Größen als Abkürzungen: | Wir verwenden dimensionslose Größen als Abkürzungen: | ||
<math>\ell_1=\lambda_1\,\ell_0, \ell_B=\lambda_2\,\ell_0, \lambda_1=1-\lambda_2, m_A=\theta_A\,m_0, m_B=\theta_B\,m_0</math>. | ::<math>\ell_1=\lambda_1\,\ell_0, \ell_B=\lambda_2\,\ell_0, \lambda_1=1-\lambda_2, m_A=\theta_A\,m_0, m_B=\theta_B\,m_0</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /************************************************************/ | ||
declare( "ℓ", alphabetic); | |||
declare( "λ", alphabetic); | |||
declare( "ϕ", alphabetic); | |||
/* system parameters */ | |||
params: [q[0] = A[0]*rho*g]; | |||
params: append(params, | |||
solve(A[0]*ℓ[0]*rho=m[0], rho)); | |||
dimless: [ℓ[1]=λ[1]*ℓ[0],ℓ[2]=λ[2]*ℓ[0],λ[1]=1-λ[2], m[A]=theta[A]*m[0], m[B]=theta[B]*m[0]]; | |||
geometry: [λ[2] = 1/3, theta[A]=1/2, theta[B]=1/2]; | |||
/* make equations of motion dim'less with load case #1 from Gross e.a., same as UEBI */ | |||
reference : [W[ref] = q[0]*ℓ[0]^4/(8*E*I[0]), ϕ[ref] = q[0]*ℓ[0]^3/(6*E*I[0]), M[ref] = m[0]*g*ℓ[0]/2, Q[ref] = m[0]*g, q[0] = m[0]*g/ℓ[0]]; | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Analytic Solution | |||
|text= | |||
Die analytische Lösung erzeugen wir aus Superpositionen der eingeprägten Lösungen zu den drei Gewichten auf die Struktur. | Die analytische Lösung erzeugen wir aus Superpositionen der eingeprägten Lösungen zu den drei Gewichten auf die Struktur. | ||
| Zeile 66: | Zeile 87: | ||
Wir nehmen das komplementäre Koordinatensystem | Wir nehmen das komplementäre Koordinatensystem | ||
<math>\bar{\xi} = 1- \xi</math> | ::<math>\bar{\xi} = 1- \xi</math> | ||
und lesen die Lösung ab: | und lesen die Lösung ab: | ||
<math>\begin{array}{lccl} | ::<math>\begin{array}{lccl} | ||
EI\,w(\bar{\xi}) &=& &\displaystyle \frac{{q_0}\, \ell_0^4 \cdot \left( 6\cdot {{\bar{\xi}}^{2}}-4\cdot {{\bar{\xi}}^{3}}+{{\bar{\xi}}^{4}}\right) }{24}\\ | EI\,w(\bar{\xi}) &=& &\displaystyle \frac{{q_0}\, \ell_0^4 \cdot \left( 6\cdot {{\bar{\xi}}^{2}}-4\cdot {{\bar{\xi}}^{3}}+{{\bar{\xi}}^{4}}\right) }{24}\\ | ||
& &+&\displaystyle \frac{m_A \, g\,\ell_0^3\cdot \left( 3\cdot {{\bar{\xi}}^{2}}-{{\bar{\xi}}^{3}}\right)}{6}\\ | & &+&\displaystyle \frac{m_A \, g\,\ell_0^3\cdot \left( 3\cdot {{\bar{\xi}}^{2}}-{{\bar{\xi}}^{3}}\right)}{6}\\ | ||
| Zeile 77: | Zeile 98: | ||
\displaystyle \frac{m_B \, g\,\ell_0^3\cdot \left( 3\cdot {{\lambda}_{2}}\cdot {{\bar{\xi}}^{2}}-{{\bar{\xi}}^{3}}+{{\left( \bar{\xi}-{{\lambda}_{2}}\right) }^{3}} \right)}{6}& \text{ sonst} | \displaystyle \frac{m_B \, g\,\ell_0^3\cdot \left( 3\cdot {{\lambda}_{2}}\cdot {{\bar{\xi}}^{2}}-{{\bar{\xi}}^{3}}+{{\left( \bar{\xi}-{{\lambda}_{2}}\right) }^{3}} \right)}{6}& \text{ sonst} | ||
\end{array}\right. | \end{array}\right. | ||
\end{array}</math>. | \end{array}</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
/**************************************************************************/ | |||
/* analytic solution */ | |||
/* ... from superposition of analytical solutions for cantileverd beam */ | |||
analySol : [q[0]*ℓ[0]^4/(24*E*I[0])*(6*xi^2-4*xi^3+xi^4), | |||
[m[B]*g*ℓ[0]^3/(6*E*I[0])*(3*xi^2*λ[2]-xi^3 + 0), | |||
m[B]*g*ℓ[0]^3/(6*E*I[0])*(3*xi^2*λ[2]-xi^3 + (xi-λ[2])^3)], | |||
m[A]*g*ℓ[0]^3/(6*E*I[0])*(3*xi^2* 1 -xi^3)]; | |||
/* obs: zwo solutions for load case 2 (weight in "B") */ | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=FE Formulation | |||
|text= | |||
Die System-Matrix setzen wir aus den Element-Steifigkeitsmatrizen aus FEM: Trial-Functions für kubische Ansatz-Polynome zusammen und arbeiten die geometrischen Randbedingungen ein, indem wir die Zeilen und Spalten bzgl der Verschiebung und Verdrehung in ''C'' (''W<sub>2</sub>, Φ<sub>2</sub>'') streichen. | Die System-Matrix setzen wir aus den Element-Steifigkeitsmatrizen aus FEM: Trial-Functions für kubische Ansatz-Polynome zusammen und arbeiten die geometrischen Randbedingungen ein, indem wir die Zeilen und Spalten bzgl der Verschiebung und Verdrehung in ''C'' (''W<sub>2</sub>, Φ<sub>2</sub>'') streichen. | ||
Das Gleichungssystem lautet dann | Das Gleichungssystem lautet dann | ||
<math>\frac{E \, I}{\ell_0^3}\cdot | ::<math>\frac{E \, I}{\ell_0^3}\cdot | ||
\begin{pmatrix}-\frac{12}{{{\lambda}_{2}^{3}}-3\cdot {{\lambda}_{2}^{2}}+3\cdot {{\lambda}_{2}}-1} & \frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & \frac{12}{{{\lambda}_{2}^{3}}-3\cdot {{\lambda}_{2}^{2}}+3\cdot {{\lambda}_{2}}-1} & \frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1}\\ \frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & -\frac{4\cdot {{\ell}_{0}^{2}}}{{{\lambda}_{2}}-1} & -\frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & -\frac{2\cdot {{\ell}_{0}^{2}}}{{{\lambda}_{2}}-1}\\ \frac{12}{{{\lambda}_{2}^{3}}-3\cdot {{\lambda}_{2}^{2}}+3\cdot {{\lambda}_{2}}-1} & -\frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & -\frac{12-36\cdot {{\lambda}_{2}}+36\cdot {{\lambda}_{2}^{2}}}{{{\lambda}_{2}^{6}}-3\cdot {{\lambda}_{2}^{5}}+3\cdot {{\lambda}_{2}^{4}}-{{\lambda}_{2}^{3}}} & -\frac{12\cdot {{\ell}_{0}}\cdot {{\lambda}_{2}}-6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{4}}-2\cdot {{\lambda}_{2}^{3}}+{{\lambda}_{2}^{2}}}\\ \frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & -\frac{2\cdot {{\ell}_{0}^{2}}}{{{\lambda}_{2}}-1} & -\frac{12\cdot {{\ell}_{0}}\cdot {{\lambda}_{2}}-6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{4}}-2\cdot {{\lambda}_{2}^{3}}+{{\lambda}_{2}^{2}}} & -\frac{4\cdot {{\ell}_{0}^{2}}}{{{\lambda}_{2}^{2}}-{{\lambda}_{2}}}\end{pmatrix} \cdot \underline{Q} = m_0\,g\cdot \begin{pmatrix}\frac{1-{{\lambda}_{2}}+2\cdot {{\theta}_{A}}}{2}\\ \frac{{{\ell}_{0}}-2\cdot {{\ell}_{0}}\cdot {{\lambda}_{2}}+{{\ell}_{0}}\cdot {{\lambda}_{2}^{2}}}{12}\\ \frac{1+2\cdot {{\theta}_{B}}}{2}\\ \frac{2\cdot {{\ell}_{0}}\cdot {{\lambda}_{2}}-{{\ell}_{0}}}{12}\end{pmatrix}</math> | \begin{pmatrix}-\frac{12}{{{\lambda}_{2}^{3}}-3\cdot {{\lambda}_{2}^{2}}+3\cdot {{\lambda}_{2}}-1} & \frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & \frac{12}{{{\lambda}_{2}^{3}}-3\cdot {{\lambda}_{2}^{2}}+3\cdot {{\lambda}_{2}}-1} & \frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1}\\ \frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & -\frac{4\cdot {{\ell}_{0}^{2}}}{{{\lambda}_{2}}-1} & -\frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & -\frac{2\cdot {{\ell}_{0}^{2}}}{{{\lambda}_{2}}-1}\\ \frac{12}{{{\lambda}_{2}^{3}}-3\cdot {{\lambda}_{2}^{2}}+3\cdot {{\lambda}_{2}}-1} & -\frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & -\frac{12-36\cdot {{\lambda}_{2}}+36\cdot {{\lambda}_{2}^{2}}}{{{\lambda}_{2}^{6}}-3\cdot {{\lambda}_{2}^{5}}+3\cdot {{\lambda}_{2}^{4}}-{{\lambda}_{2}^{3}}} & -\frac{12\cdot {{\ell}_{0}}\cdot {{\lambda}_{2}}-6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{4}}-2\cdot {{\lambda}_{2}^{3}}+{{\lambda}_{2}^{2}}}\\ \frac{6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{2}}-2\cdot {{\lambda}_{2}}+1} & -\frac{2\cdot {{\ell}_{0}^{2}}}{{{\lambda}_{2}}-1} & -\frac{12\cdot {{\ell}_{0}}\cdot {{\lambda}_{2}}-6\cdot {{\ell}_{0}}}{{{\lambda}_{2}^{4}}-2\cdot {{\lambda}_{2}^{3}}+{{\lambda}_{2}^{2}}} & -\frac{4\cdot {{\ell}_{0}^{2}}}{{{\lambda}_{2}^{2}}-{{\lambda}_{2}}}\end{pmatrix} \cdot \underline{Q} = m_0\,g\cdot \begin{pmatrix}\frac{1-{{\lambda}_{2}}+2\cdot {{\theta}_{A}}}{2}\\ \frac{{{\ell}_{0}}-2\cdot {{\ell}_{0}}\cdot {{\lambda}_{2}}+{{\ell}_{0}}\cdot {{\lambda}_{2}^{2}}}{12}\\ \frac{1+2\cdot {{\theta}_{B}}}{2}\\ \frac{2\cdot {{\ell}_{0}}\cdot {{\lambda}_{2}}-{{\ell}_{0}}}{12}\end{pmatrix}</math> | ||
mit | mit | ||
<math>\underline{Q} = \left( | ::<math>\underline{Q} = \left( | ||
\begin{array}{c} | \begin{array}{c} | ||
W_0\\ | W_0\\ | ||
| Zeile 104: | Zeile 132: | ||
\Phi_1\\ | \Phi_1\\ | ||
\end{array} | \end{array} | ||
\right)</math>. | \right)</math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1+1 | /**************************************************************************/ | ||
/* FE Formulation */ | |||
/* element matrices */ | |||
K[i] : (E*I[0]/ℓ[i]^3)*matrix([12,6*ℓ[i],-12,6*ℓ[i]], | |||
[6*ℓ[i],4*ℓ[i]^2,-6*ℓ[i],2*ℓ[i]^2], | |||
[-12,-6*ℓ[i],12,-6*ℓ[i]], | |||
[6*ℓ[i],2*ℓ[i]^2,-6*ℓ[i],4*ℓ[i]^2]); | |||
P[i] : rho*A[0]*g*ℓ[i]*matrix([ 1/2 ], | |||
[ ℓ[i]/12], | |||
[ 1/2 ], | |||
[-ℓ[i]/12]); | |||
/* use one element per section */ | |||
NOE : 2; /* number of elements */ | |||
NON : NOE+1; /* number of nodes */ | |||
xCoord: subst(geometry,[0,1-λ[2],1]); | |||
/* define both element matrices */ | |||
for e:1 thru NOE do ( | |||
K[e] : ratsimp(subst(dimless,subst([ℓ[e]=ℓ[0]*λ[e]], subst([i=e], K[i])))), | |||
P[e] : ratsimp(subst(dimless,subst([ℓ[e]=ℓ[0]*λ[e]], subst([i=e], P[i]))))); | |||
/* compose system matrix */ | |||
K[0] : zeromatrix(2*NON,2*NON); | |||
P[0] : zeromatrix(2*NON,1); | |||
for ele:1 thru NOE do ( | |||
for row:1 thru 4 do ( | |||
P[0][2*(ele-1)+row,1] : P[0][2*(ele-1)+row,1] + P[ele][row,1], | |||
for col:1 thru 4 do ( | |||
K[0][2*(ele-1)+row,2*(ele-1)+col] : K[0][2*(ele-1)+row,2*(ele-1)+col] + K[ele][row,col]))); | |||
P[0] : ratsimp(subst(params,P[0])); | |||
/* add discrete loads an points A and B */ | |||
P[0][1,1] : P[0][1,1]+m[A]*g; | |||
P[0][3,1] : P[0][3,1]+m[B]*g; | |||
/* incorporate bounday conditions */ | |||
AA : submatrix(5,6,K[0],5,6); | |||
bb : submatrix(5,6,P[0]); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
== | <!--------------------------------------------------------------------------------> | ||
Lösen des linearen Gleichungssystems liefert | |||
{{MyCodeBlock|title=Solving | |||
|text=Lösen des linearen Gleichungssystems liefert | |||
<math>\begin{array}{ccl} | ::<math>\begin{array}{ccl} | ||
\displaystyle \frac{W_0}{W_{ref}}&=&\displaystyle -\frac{-3-8\cdot {{\theta}_{A}}+\left( 4\cdot {{\lambda}_{2}^{3}}-12\cdot {{\lambda}_{2}^{2}}\right) \cdot {{\theta}_{B}}}{3}\\ | \displaystyle \frac{W_0}{W_{ref}}&=&\displaystyle -\frac{-3-8\cdot {{\theta}_{A}}+\left( 4\cdot {{\lambda}_{2}^{3}}-12\cdot {{\lambda}_{2}^{2}}\right) \cdot {{\theta}_{B}}}{3}\\ | ||
\displaystyle \frac{\Phi_0}{W_{ref}}&=&\displaystyle -\frac{4+12\cdot {{\theta}_{A}}+12\cdot {{\lambda}_{2}^{2}}\cdot {{\theta}_{B}}}{3\cdot {{\ell}_{0}}}\\ | \displaystyle \frac{\Phi_0}{W_{ref}}&=&\displaystyle -\frac{4+12\cdot {{\theta}_{A}}+12\cdot {{\lambda}_{2}^{2}}\cdot {{\theta}_{B}}}{3\cdot {{\ell}_{0}}}\\ | ||
| Zeile 125: | Zeile 195: | ||
\displaystyle \frac{\Phi_2}{W_{ref}}&=& 0 | \displaystyle \frac{\Phi_2}{W_{ref}}&=& 0 | ||
\end{array} | \end{array} | ||
</math>. | </math>. | ||
|code= | |code= | ||
<syntaxhighlight lang="lisp" line start=1> | <syntaxhighlight lang="lisp" line start=1> | ||
1 | /***************************************************************************/ | ||
/* solve */ | |||
sol: ratsimp(subst(dimless,linsolve_by_lu(AA,bb)))[1]; | |||
nodalSol: ratsimp(subst(dimless,subst(reference,flatten(append( | |||
makelist( | |||
[ W [i-1] = sol[2*i-1][1], | |||
Phi[i-1] = sol[2*i ][1]],i,1,NOE), | |||
[ W [ 2] = 0 , | |||
Phi[ 2] = 0 ]))))); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
= | <!--------------------------------------------------------------------------------> | ||
{{MyCodeBlock|title=Post-Processing | |||
|text= | |||
Und die Ergebnisse der analytischen und FE-Rechnungen plotten wir ... | Und die Ergebnisse der analytischen und FE-Rechnungen plotten wir ... | ||
| Zeile 149: | Zeile 227: | ||
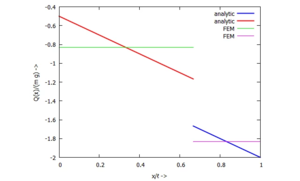
==== ... für Q(x): ==== | ==== ... für Q(x): ==== | ||
[[Datei:Kw60-24.png|mini|Querkraft ''Q(x)''|alternativtext=|ohne]] | [[Datei:Kw60-24.png|mini|Querkraft ''Q(x)''|alternativtext=|ohne]] | ||
|code= | |||
<syntaxhighlight lang="lisp" line start=1> | |||
/***************************************************************************/ | |||
/* plot results */ | |||
/* Trial-Fucntions */ | |||
phi : [ (xi-1)^2*(2*xi+1), | |||
ℓ[i]* xi *( xi-1)^2, | |||
- xi^2 *(2*xi-3), | |||
ℓ[i]* xi^2 *( xi-1)]; | |||
< | textlabels : ["<- w(x)/w[ref]", "<- w'(x)/ϕ[ref]", "M(x)/(m*g*ℓ/2) ->", "Q(x)/(m g) ->"]; | ||
for D:0 thru 3 do ( | |||
/* pick a reference value to plot dimensionless */ | |||
Ref : [W[ref], ϕ[ref], M[ref], Q[ref]][D+1], | |||
Fac : [ 1 , 1 ,-E*I[0],-E*I[0]][D+1], | |||
toPlotFEM : makelist([parametric, | |||
xCoord[e]*(1-t)+xCoord[e+1]*t, | |||
expand(subst([xi=t],subst(geometry,subst(reference,subst(nodalSol,subst(dimless, subst([i=e], | |||
Fac*diff(sum( [W[i-1],Phi[i-1],W[i],Phi[i]][j]*phi[j],j,1,4),xi,D)/ℓ[i]^D/Ref | |||
))))))), | |||
[t,0,1]],e,1,NOE), | |||
toPlotAly : subst(geometry,subst([xi=t], | |||
[[parametric, 1-xi,(-1)^D*ratsimp(Fac*diff(subst(geometry,subst(reference,subst(dimless,(analySol[1]+analySol[2][1]+analySol[3])/Ref))),xi,D)/ℓ[0]^D), [t,0,λ[2]]], | |||
[parametric, 1-xi,(-1)^D*ratsimp(Fac*diff(subst(geometry,subst(reference,subst(dimless,(analySol[1]+analySol[2][2]+analySol[3])/Ref))),xi,D)/ℓ[0]^D), [t,λ[2],1]]])), | |||
toPlot: append(toPlotAly,toPlotFEM), | |||
preamble: if D<=1 then "set yrange [] reverse" else "set yrange []", | |||
plot2d(toPlot, [legend, "analytic", "analytic", "FEM", "FEM"], | |||
[gnuplot_preamble, preamble], | |||
[style, [lines, 2],[lines, 2],[lines, 1],[lines, 1]], | |||
[xlabel, "x/ℓ ->"], | |||
[ylabel, textlabels[D+1]])); | |||
</syntaxhighlight> | </syntaxhighlight> | ||
}} | }} | ||
Version vom 31. März 2021, 09:43 Uhr
Aufgabenstellung
Der Euler-Bernoulli-Balken ABC (Länge ℓ0, Biegesteifigkeikeit EI, Querschnittsflläche A) ist am rechten Rand fest eingespannt und wird durch das Gewicht
- aufgrund seiner eigenen Masse m0 sowie
- aufgrund von zwei Personen der Massen mA bzw. mB
belastet.
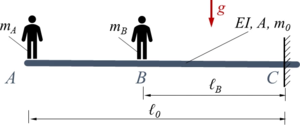
Gesucht ist eine Näherungslösung mit der Methode der Finiten Elemente und zwei Elementen. Dabei sollen die Verläufe der Biegelinie und die Schnittlasten mit der analytischen Lösung verlglichen werden.
Es ist ℓB = ℓ0 /3, mA = m0 /2 und mB = m0 /2.
Lösung mit Maxima
Header
Das Modell erstellen wir mit der FEM-Formulierung für den Euler-Bernoulli-Balken mit zwei Elementen.
/*******************************************************/
/* MAXIMA script */
/* version: wxMaxima 15.08.2 */
/* author: Andreas Baumgart */
/* last updated: 2019-09-01 */
/* ref: TMC */
/* description: simple EBB with two section */
/* solved as FE Problem */
/*******************************************************/
Declarations
Zum späteren Plotten verwenden wir Referenzgrößen, die wir der analytischen Standard-Lösung eines Kragbalkens entnehmen.
Dies sind
- .
Wir verwenden dimensionslose Größen als Abkürzungen:
- .
/************************************************************/
declare( "ℓ", alphabetic);
declare( "λ", alphabetic);
declare( "ϕ", alphabetic);
/* system parameters */
params: [q[0] = A[0]*rho*g];
params: append(params,
solve(A[0]*ℓ[0]*rho=m[0], rho));
dimless: [ℓ[1]=λ[1]*ℓ[0],ℓ[2]=λ[2]*ℓ[0],λ[1]=1-λ[2], m[A]=theta[A]*m[0], m[B]=theta[B]*m[0]];
geometry: [λ[2] = 1/3, theta[A]=1/2, theta[B]=1/2];
/* make equations of motion dim'less with load case #1 from Gross e.a., same as UEBI */
reference : [W[ref] = q[0]*ℓ[0]^4/(8*E*I[0]), ϕ[ref] = q[0]*ℓ[0]^3/(6*E*I[0]), M[ref] = m[0]*g*ℓ[0]/2, Q[ref] = m[0]*g, q[0] = m[0]*g/ℓ[0]];
Analytic Solution
Die analytische Lösung erzeugen wir aus Superpositionen der eingeprägten Lösungen zu den drei Gewichten auf die Struktur.
Dazu müssen wir ein bisschen umdenken: in den Standard-Lösungen ist der Balken jeweils links fest eingespannt - hier rechts.
Wir nehmen das komplementäre Koordinatensystem
und lesen die Lösung ab:
- .
/**************************************************************************/
/* analytic solution */
/* ... from superposition of analytical solutions for cantileverd beam */
analySol : [q[0]*ℓ[0]^4/(24*E*I[0])*(6*xi^2-4*xi^3+xi^4),
[m[B]*g*ℓ[0]^3/(6*E*I[0])*(3*xi^2*λ[2]-xi^3 + 0),
m[B]*g*ℓ[0]^3/(6*E*I[0])*(3*xi^2*λ[2]-xi^3 + (xi-λ[2])^3)],
m[A]*g*ℓ[0]^3/(6*E*I[0])*(3*xi^2* 1 -xi^3)];
/* obs: zwo solutions for load case 2 (weight in "B") */
FE Formulation
Die System-Matrix setzen wir aus den Element-Steifigkeitsmatrizen aus FEM: Trial-Functions für kubische Ansatz-Polynome zusammen und arbeiten die geometrischen Randbedingungen ein, indem wir die Zeilen und Spalten bzgl der Verschiebung und Verdrehung in C (W2, Φ2) streichen.
Das Gleichungssystem lautet dann
mit
- .
/**************************************************************************/
/* FE Formulation */
/* element matrices */
K[i] : (E*I[0]/ℓ[i]^3)*matrix([12,6*ℓ[i],-12,6*ℓ[i]],
[6*ℓ[i],4*ℓ[i]^2,-6*ℓ[i],2*ℓ[i]^2],
[-12,-6*ℓ[i],12,-6*ℓ[i]],
[6*ℓ[i],2*ℓ[i]^2,-6*ℓ[i],4*ℓ[i]^2]);
P[i] : rho*A[0]*g*ℓ[i]*matrix([ 1/2 ],
[ ℓ[i]/12],
[ 1/2 ],
[-ℓ[i]/12]);
/* use one element per section */
NOE : 2; /* number of elements */
NON : NOE+1; /* number of nodes */
xCoord: subst(geometry,[0,1-λ[2],1]);
/* define both element matrices */
for e:1 thru NOE do (
K[e] : ratsimp(subst(dimless,subst([ℓ[e]=ℓ[0]*λ[e]], subst([i=e], K[i])))),
P[e] : ratsimp(subst(dimless,subst([ℓ[e]=ℓ[0]*λ[e]], subst([i=e], P[i])))));
/* compose system matrix */
K[0] : zeromatrix(2*NON,2*NON);
P[0] : zeromatrix(2*NON,1);
for ele:1 thru NOE do (
for row:1 thru 4 do (
P[0][2*(ele-1)+row,1] : P[0][2*(ele-1)+row,1] + P[ele][row,1],
for col:1 thru 4 do (
K[0][2*(ele-1)+row,2*(ele-1)+col] : K[0][2*(ele-1)+row,2*(ele-1)+col] + K[ele][row,col])));
P[0] : ratsimp(subst(params,P[0]));
/* add discrete loads an points A and B */
P[0][1,1] : P[0][1,1]+m[A]*g;
P[0][3,1] : P[0][3,1]+m[B]*g;
/* incorporate bounday conditions */
AA : submatrix(5,6,K[0],5,6);
bb : submatrix(5,6,P[0]);
Solving
Lösen des linearen Gleichungssystems liefert
- .
/***************************************************************************/
/* solve */
sol: ratsimp(subst(dimless,linsolve_by_lu(AA,bb)))[1];
nodalSol: ratsimp(subst(dimless,subst(reference,flatten(append(
makelist(
[ W [i-1] = sol[2*i-1][1],
Phi[i-1] = sol[2*i ][1]],i,1,NOE),
[ W [ 2] = 0 ,
Phi[ 2] = 0 ])))));
Post-Processing
Und die Ergebnisse der analytischen und FE-Rechnungen plotten wir ...
... für w(x):
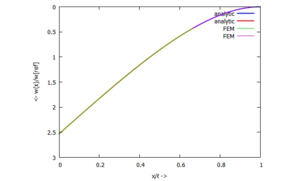
... für Φ(x):
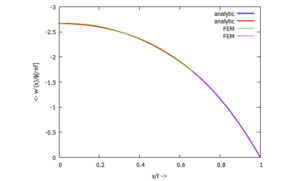
... für M(x):
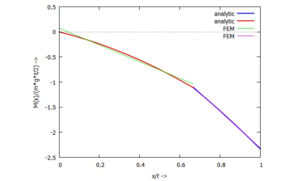
... für Q(x):
/***************************************************************************/
/* plot results */
/* Trial-Fucntions */
phi : [ (xi-1)^2*(2*xi+1),
ℓ[i]* xi *( xi-1)^2,
- xi^2 *(2*xi-3),
ℓ[i]* xi^2 *( xi-1)];
textlabels : ["<- w(x)/w[ref]", "<- w'(x)/ϕ[ref]", "M(x)/(m*g*ℓ/2) ->", "Q(x)/(m g) ->"];
for D:0 thru 3 do (
/* pick a reference value to plot dimensionless */
Ref : [W[ref], ϕ[ref], M[ref], Q[ref]][D+1],
Fac : [ 1 , 1 ,-E*I[0],-E*I[0]][D+1],
toPlotFEM : makelist([parametric,
xCoord[e]*(1-t)+xCoord[e+1]*t,
expand(subst([xi=t],subst(geometry,subst(reference,subst(nodalSol,subst(dimless, subst([i=e],
Fac*diff(sum( [W[i-1],Phi[i-1],W[i],Phi[i]][j]*phi[j],j,1,4),xi,D)/ℓ[i]^D/Ref
))))))),
[t,0,1]],e,1,NOE),
toPlotAly : subst(geometry,subst([xi=t],
[[parametric, 1-xi,(-1)^D*ratsimp(Fac*diff(subst(geometry,subst(reference,subst(dimless,(analySol[1]+analySol[2][1]+analySol[3])/Ref))),xi,D)/ℓ[0]^D), [t,0,λ[2]]],
[parametric, 1-xi,(-1)^D*ratsimp(Fac*diff(subst(geometry,subst(reference,subst(dimless,(analySol[1]+analySol[2][2]+analySol[3])/Ref))),xi,D)/ℓ[0]^D), [t,λ[2],1]]])),
toPlot: append(toPlotAly,toPlotFEM),
preamble: if D<=1 then "set yrange [] reverse" else "set yrange []",
plot2d(toPlot, [legend, "analytic", "analytic", "FEM", "FEM"],
[gnuplot_preamble, preamble],
[style, [lines, 2],[lines, 2],[lines, 1],[lines, 1]],
[xlabel, "x/ℓ ->"],
[ylabel, textlabels[D+1]]));
Links
- ...
Literature
- ...